Begnadete Körper

Carsten Dachsbacher/Nils Pipenbrinck

Ein komplexer drei­dimensionaler Körper läßt sich nur sehr schwer im zwei­dimensionalen Speicher­bereich Ihres Rechners nachbilden – so scheint es auf den ersten Blick. Doch im Prinzip bestehen 3D-Objekte lediglich aus Punkten (Vertices, Singularform: Vertex) und Polygonen (Faces).

Zur Vereinfachung beschränkt sich die 3D-Engine auf die Darstellung von Dreiecken dieser Ausgabe. Am einfachsten ist es, eine Struktur oder ein Objekt zu erzeugen, das Vertices und Faces voneinander getrennt in zwei Arrays speichert.

Ein Vertex ist ein Ortsvektor, der die Position des Punktes im Raum angibt. Ein Vektor und ein Vertex sind also von der Struktur her identisch. Heißt es im Text Vertices, sind damit Eckpunkte des 3D-Objekts gemeint. Finden Sie den Ausdruck Vektor, handelt es sich um einen Wert, mit dem gerechnet wird.

Für ein Face brauchen Sie mehr Informationen: Neben den Indizes der Vertices, die das Dreieck aufspannen, sind noch dessen Farbe und ein paar andere Daten interessant.

3D-Engines sind einfach aufgebaut: Alle auf Polygonen basierenden Engines verwenden eine nahezu identische Hauptschleife – im Fachjargon „Pipeline“ genannt. Die Standard-Pipeline arbeitet in fünf Schritten.
• Sie trans­formiert die Objekt-Geometrie vom Objekt- in das Welt-Koordinaten­system,
• entfernt nicht sichtbare Polygone (Backface Culling),
• berechnet die Beleuchtung (Shading),
• schneidet den nicht sichtbaren Bereich ab (Clipping)
• und zeichnet die Polygone (Rendering).

Anfangs ist etwas Grundwissen in linearer Algebra und Matrizen-Rechnung nötig. In den Formeln beschreibt ⨯ das Kreuzprodukt (zwei­dimensionales Vektor­projekt) und O das Skalar­produkt (drei­dimensionales Vektor­produkt) zweier Vektoren.

Transformationen

Da Sie im Moment noch keine frei bewegliche Kamera für die Engine benötigen, sind Trans­formationen wie Drehungen, Größen­änderungen und Ver­schiebungen relativ einfach zu realisieren. Stellen Sie diese Operationen in der Matrix-Schreib­weise dar. Das ist sehr über­sichtlich und spart viel Zeit bei der Berechnung. Die Rotation eines Vektors um die z-Achse mit dem Rotations­winkel ϕ beschreibt die Matrix 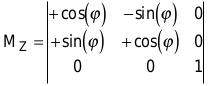Möchten Sie einen Punkt a um die z-Achse rotieren lassen, multi­plizieren Sie ihn mit dieser Matrix. Die Ko­ordinaten des Ziel­punktes b erhalten Sie über die einzelnen Rechen­schritte:
b.x=a.x*cos(ϕ)-a.y*sin(ϕ)+a.z*0
b.y=a.x*sin(ϕ)+a.y*cos(ϕ)+a.z*0
b.z=a.x*0+a.y*0+a.z*1
Die Rotations­matrizen für die y- und x-Achse sehen ähnlich aus: 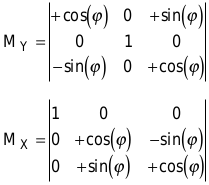Sie brauchen nicht jeden Punkt nacheinander mit allen drei Matrizen multi­plizieren. Wenn Sie zunächst das Produkt aus den Matrizen bilden, erhalten Sie eine Matrix für alle drei Trans­formationen.

Für wenige Punkte lohnt sich dieser Aufwand sicher­lich nicht, da eine Matrizen-Multi­plikation sehr viel Rechen­aufwand benötigt. Bereits einfache Objekte besitzen aber meist schon über 200 Vertices. Daher beschleunigt die Kombi­nation der Matrizen die Berechnung erheblich.

Die Darstellung der ausmulti­plizierten Rotations­matrix sei Ihnen an dieser Stelle erspart. Im Code der 3D-Engine finden Sie eine Routine, die diese Matrix direkt berechnet.

Die zweite, auf Objekte gerichtete Operation ist die Skalierung. Mit der Matrix 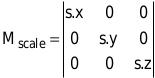ver­größern und ver­kleinern Sie Objekte um den Skalierungs­faktor s.

Die Translation (Verschiebung) stellt Sie zunächst vor das Problem, die geeignete Matrix dafür zu finden. Der Trick besteht darin, die 3x3-Matrix auf eine 4x4-Matrix zu erweitern und jeden Vektor um eine vierte (nicht benutzte) Komponente zu vergrößern.

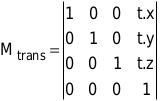
Natürlich können Sie keinen 3D-Vektor mit einer 4x4-Matrix multi­plizieren. Deshalb fügen Sie dem Vektor eine vierte Kom­ponente hinu, die immer den Wert 1 besitzt.

Auch die alten 3x3-Matrizen schreiben Sie einfach in 4x4-Matrizen um:

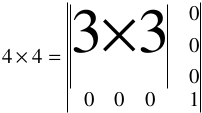
Im Quell­text von 3dengine.cpp bildet tobject::build_ltm (void) die lokale Trans­formations­matrix.

Backface Culling

In der 3D-Grafik geht man davon aus, daß Polygone einseitig sind. Sie besitzen also nur eine Vorder- und eine Rück­seite. Dieser kleine Trick spart bereits bis zu 50 Prozent Rechen­zeit ein.

Nehmen Sie als Beispiel einen Würfel. Von außen betrachtet, sehen Sie nur seine Außen­seiten. Bei der Darstellung als 3D-Objekt wäre es daher sinnlos, die immer durch eine andere Vorder­seite verdeckten Polygone an der Rück­seite des Würfels zu zeichnen.

Ob ein Polygon sichtbar ist oder nicht, finden Sie mit einfacher Vektor­arithmetik heraus. Zunächst ermitteln Sie den sogenannten Normalen­vektor des Polygons: Er steht im rechten Winkel auf dem Polygon. Sind A, B und C die Vertices der Polygon­ebene, errechnen Sie ihn einfach aus dem Kreuz­produkt

Normalenvektor = [C-A] ⨯ [C-B]
Das Ergebnis normieren Sie auf die Länge 1, indem Sie jede Kom­ponente durch die Länge des Vektors dividieren. Da die Blick­richtung der Kamera der z-Achse entspricht, finden Sie recht einfach heraus, ob das Polygon sichtbar ist oder nicht: Sobald der z-Anteil des Normalenvektors positiv ist, kann der Betrachter es nicht mehr sehen. Ein kleines Problem gibt es bei diesem Verfahren: Das Objekt wird trans­formiert. Um Drehung, Skalierung und Ver­schiebung auszugleichen, müßte man die Trans­formation auf die Normalen­vektoren anwenden oder diese für jedes Bild neu ermitteln. Beides kostet sehr viel Rechen­zeit.

Berechnen Sie die Sicht­barkeit der Faces deshalb vor der Drehung der Punkte. Dazu benötigen Sie zunächst die Inverse der Trans­formations­matrix, die deren Aktionen wieder rückgängig macht. Als Beispiel nehmen wir die Matrix M, die zunächst einen Punkt 30 Grad um die z-Achse dreht und dann um den Vektor <1,2,3> verschiebt. Die Inverse dieser Matrix verschiebt zunächst den Punkt um <-1,-2,-3> und rotiert dann mit -30 Grad um die z-Achse. Wichtig: Die Inverse kehrt nicht nur die Vor­zeichen der Werte um, sondern auch die Reihen­folge der Operationen.

Mit der inversen Matrix multi­plizieren Sie jetzt die Position der Kamera, die bei festem Kamera­stand­punkt im Ursprung <0,0,0> liegt:

Lokale Kamera := ( <0,0,0> * Inverse Matrix )
So erhalten Sie die vom Objekt aus gesehene Position der Kamera.

Diese recht aufwendige Matrix-Inversion berechnet die Funktion angle_perserving_matrix_inverse in 3dmath.cpp. Die dort benutzte Imple­mentation von Kevin Wu¹ ist für die in der 3D-Grafik vorkommenden Matrizen optimiert und sehr schnell. Sie funktioniert jedoch ausschließlich mit aus Rotationen, Skalierungen und Trans­lation berechneten 4x4-Matrizen.

Da Sie die Kamera­position rückwärts transformiert haben, brauchen Sie für den Sicht­barkeits­test die Trans­formation des Objekts nicht mehr zu beachten. Das Polygon zeigt mit seiner Vorder­seite dann zum Betrachter, wenn gilt:

(Normalenvektor O Lokale Kamera) >= (Normalenvektor O a)
Dabei ist a ein beliebiger, nicht­trans­formierter Vertex des Face.

Der Normalen­vektor und somit auch der Normalen­vektor O a ist für jedes Polygon konstant. Daher berechnet die Routine tobject::calc_ facenormals() diese Werte vor dem ersten Zeichnen des Objekts und speichert sie in der Polygon­struktur.

Es werde Licht

Die 3D-Engine dieser Ausgabe beherrscht vorläufig lediglich Flat-Shading: die einfachste Art der Be­leuchtung. Den Anteil des einfallenden Lichts berechnen Sie direkt aus dem Normalen­vektor des Polygons und dem Vektor der Einfalls­richtung des Lichts (Licht­vektor).

Um sich die Arbeit zu erleichtern, gehen Sie davon aus, daß die Licht­quelle unendlich weit vom Objekt entfernt ist. Dann können Sie das Licht als Einfalls­vektor definieren und brauchen ihn nicht für jede Fläche neu zu berechnen. Den Beleuchtungs­wert ermitteln Sie mit der Formel 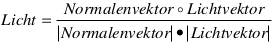Die Normalen­vektoren sind schon während der Objekt­initialisierung auf die Länge 1 eingestellt. Ist auch der Licht­vektor normalisiert, können Sie die Beleuchtungs­formel vereinfachen, indem Sie den Nenner entfernen:

Licht = Normalenvektor O Lichtvektor.
Bleibt noch ein Problem: Sie müssen wieder die Trans­formation des Objekts in Betracht ziehen, sonst rotiert die Licht­quelle mit dem Objekt. Wie bei der Entfernung der unsichtbaren Faces kürzen Sie den Prozeß ab und trans­formieren den Licht­vektor einmal mit der inversen Rotations­matrix. Mit der so berechneten Licht­intensität schattieren Sie – wie bereits in PC Underground der letzten Ausgabe (ab S. 228) beschrieben – den Farbwert des Polygons. Dieses einfache Beleuchtungs­modell ist schon sehr effektiv und bringt eine Menge Leben in die 3D-Szene.

Clipping

Nun haben Sie zwar eine Menge Be­rechnungen durchgeführt, aber noch immer ist der Bild­schirm leer. Haben Sie noch etwas Geduld, eine Hürde ist noch zu überwinden: das Clipping. Gerade in diesem Bereich gibt es viele verschiedene Lösungs­ansätze. Wir stellen Ihnen das elegante 3D-Clipping-Verfahren vor.

Was bedeutet Clipping? Stellen Sie sich vor, Sie haben ein Polygon trans­formiert und möchten es jetzt zeichnen. Die z-Koordinate eines Punkts könnte den Wert 0 bekommen. Da aber die Position des Betrachters genau auf der Ebene mit dem z-Anteil 0 liegt, wären erhebliche Dar­stellungs­fehler die Folge.

„Schneiden“ Sie deshalb zunächst einmal alle Teile des Polygons ab, die vor der Z-Near-Clipping-Grenze liegen. Diese frei wählbare (positive) Grenze gibt die Ent­fernung an, bis zu der Poly­gone sichtbar sind. Teile, die näher am Betrachter liegen, werden „geclipped“. Um die berechneten 3D-Welten auf den zwei­dimensionalen Monitor zu projizieren, verwenden Sie die beiden Gleichungen

Bild.x = (Vektor.x * Projektionsfaktor) / Vektor.z + Bildbreite / 2
Bild.y = (Vektor.y * Projektionsfaktor) / Vektor.z + Bildhöhe / 2
		

Diese Formeln zeigen, daß z-Werte nicht gleich 0 sein dürfen. Eine Division durch 0 würde unweigerlich zum Programm­absturz führen.

Diese Gleichungen erzeugen auch Ko­ordinaten, die außerhalb des Bild­bereichs liegen. Sie könnten jetzt eine Polygon­routine zum Zeichnen benutzen, die mit nicht geclippten Poly­gonen umgehen kann. Das wäre jedoch nicht sehr effi­zient. Sinn­voll und sauberer ist es, die Polygone schon vor dem Zeichnen auf den sicht­baren Bildschirm­bereich zurecht­zustutzen.

Der für den Betrachter sichtbare Bereich ist eine viereckige Pyramide, die vom Kamera­stand­punkt aus aufgespannt wird. Aus der Projektions­formel berechnen Sie direkt die Ebenen, die diese Pyramide bilden. Das erledigt die Funktion Setup_Fustrum() in der Datei 3dclip.cpp.

Für das Clipping an einer Ebene benötigen Sie den zugehörigen Normalen­vektor und den Abstand der Ebene Z-Near vom Ursprung – alle anderen Ebenen gehen durch den Ur­sprung und haben daher den Abstand 0.

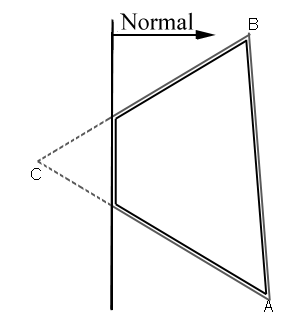
Berechnen Sie zunächst für jeden Punkt des Face den Abstand zur Ebene:

Abstand = (Ebenennormale O Vertex) - (Ebenenabstand zum Ursprung)

Anschließend können Sie in einer Schleife alle Punkte und die Linie vom aktuellen zum nächsten Punkt betrachten Punkt A in der Beispiels­kizze liegt innerhalb des Sicht­bereichs – Clipping ist nicht erforderlich. Mit Punkt C sieht das anders aus. Berechnen Sie die Schnitt­punkte der Verbindungs­strecke von A nach C sowie von B nach C mit der Ebene, und fügen Sie diese zusätzlichen Punkte anstelle von C in Ihr Polygon ein.

Wie Sie sehen, hat das fertige Polygon jetzt vier Eck­punkte. Das stellt jedoch kein Problem dar, da Sie das Polygon vor dem Zeichnen wieder in Drei­ecke zerlegen können. Nachdem Sie das Polygon mit der ersten Ebene geschnitten haben, fahren Sie an der nächsten Ebene fort.

Wieder­holen Sie diesen Vorgang für alle Ebenen. Taucht dabei ein „de­generiertes“ Polygon mit weniger als drei Eck­punkten auf, brechen Sie den Vorgang für dieses Polygon ab und ignorieren es einfach. Dieser Fall tritt dann ein, wenn ein Polygon komplett auf der un­sichtbaren Seite einer Ebene liegt, aber einer oder zwei der Eck­punkte auf einer Clipping-Ebene.

Rendering

Zeichnen Sie ein Polygon zeilen­weise. Für jede Bildschirm­zeile berechnen Sie den linken und den rechten Rand des Polygons und setzen die Pixel dazwischen (Scanline) mit den ein­gestellten Parametern. Diese Parameter sagen zum Beispiel aus, ob das Polygon einfarbig, mit Helligkeits­werten oder mit einer Textur belegt sein soll. Momentan beschränken wir uns auf das Grund­gerüst einer einfachen 3D-Engine und zeichnen nur Polygone mit einer einheitlichen Farbe.

Der erste Schritt besteht darin, den obersten und den untersten Eck­punkt herauszufinden. Dazu suchen Sie einfach nach den Punkten mit minimalem und maximalem y-Wert. Als Beispiel soll folgendes Polygon dienen, dessen Eck­punkte zum Zeichnen gegen den Uhrzeiger­sinn angeordnet sein müssen:

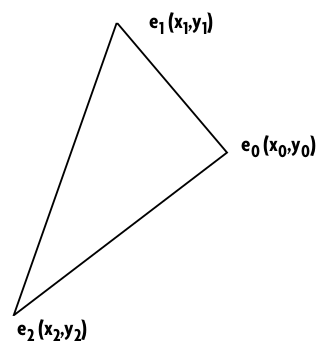
Hier ist e₁ der oberste Eck­punkt und e₂ der unterste. Nach dem Setzen von e₁ suchen Sie an der linken Kante des Polygons den nächsten Start­punkt der Scan­line. Dazu betrachten Sie die Eck­punkte mit steigendem Index (hier e₂). Auf der rechten Seite gilt es, den Punkt mit dem nächst­niedrigeren Index zu finden (hier zuerst e₀, dann e₂). Beachten Sie, daß der nächst­höhere Punkt zu e₂ wieder e₀ ist und analog dazu e₂ der nächst­niedrigere zu e₀.

Für das Beispiel­polygon ergeben sich zwei Kanten­züge:

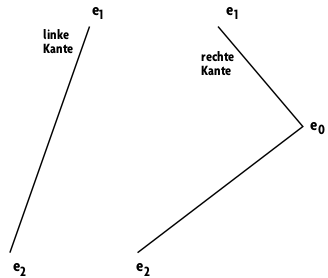
Beginnend beim obersten Eck berechnen Sie die Steigung der x-Komponente für den rechten Kanten­zug (von e₁ nach e₀) – also die Zahl der Pixel, um die sich die x-Koordinate der Kante pro Zeile verschiebt. Kanten­abschnitte der Höhe 0 ignorieren Sie einfach. Die Steigung für den ersten rechten Kanten­zug ist also
dx = (x0 - x1) / (y0 - y1) Diese Steigung addieren Sie bei jedem Sprung in eine neue Scanline zum aktuellen x-Wert. Dadurch erreichen Sie eine enorme Geschwindig­keits­steigerung gegenüber der direkten Berechnung der Kanten anhand der Eckpunkt­koordinaten.

Berechnen Sie dann die Steigung für den ersten Teil der linken Kante. Besitzen alle Kanten­abschnitte die Höhe 0, ist die Gesamt­höhe ebenfalls gleich 0 und das Polygon somit unsichtbar. Beginnen Sie damit, die x-Werte entlang der Kanten zu inter­polieren und die Scan­lines zu zeichnen.

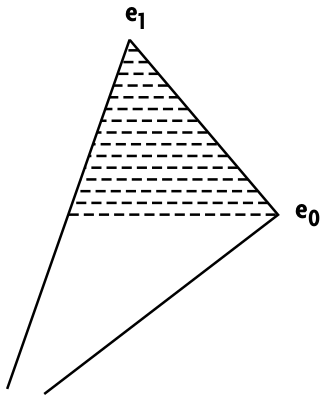
Ist das Ende eines Abschnitts erreicht, suchen Sie den nächsten mit einer Höhe größer als 0, berechnen die Steig­ungen und zeichnen die ver­bleibenden Scan­lines. Sind Sie beim untersten Punkt an­gelangt, ist das Polygon voll­ständig gezeichnet.

Der Z-Buffer

Bei der Anzeige am Bild­schirm darf kein Polygon ein zuvor ge­zeichnetes über­decken, das dem Betrachter näher steht. Am ein­fachsten stellt dies der sogenannte Maler-Algorithmus sicher. Er sortiert alle Polygone nach der Entfernung zum Betrachter und zeichnet dann die weiter entfernten zuerst. Körper, die sich überschneiden oder räumlich gesehen sowohl vor als auch hinter anderen liegen, verursachen bei diesem Verfahren allerdings grobe Dar­stellungs­fehler.

3D-Grafik­karten greifen deshalb auf den Z-Buffer-Algorithmus zurück. Er berechnet für jedes zu zeichnende Pixel die Entfernung des aktuellen Polygons zu eventuell vorher gezeichneten Polygonen an dieser Stelle. Ein neuer Pixel erscheint nur, wenn er näher am Betrachter liegt.

Wenn Sie die Polygon­routine mit einer Z-Buffer-Implementierung programmieren, belegen Sie einen Speicher­bereich (Z-Buffer), der für jeden Bildpunkt eine 16 Bit große Ent­fernungs­variable reserviert.

Wie aber bestimmen Sie die Entfernung eines Polygons zum Betrachter aneinem bestimmten Punkt innerhalb des Polygons? Ganz einfach: Diesen Wert interpolieren Sie genauso wie die x-Koordinate der Polygon­kante entlang einer Kante. Dann benötigen Sie nur noch ein Inkrement, das die Änderung der Entfernung entlang einer Scanline bestimmt.

Aus zwei Gründen ist es sinnvoll, nicht die Ent­fernung direkt zu inter­polieren, sondern mit ihrem Kehr­wert zu arbeiten:
• Zum einen ist der Kehr­wert per­pektivisch korrekt (anderenfalls können bei sich schneidenden Polygonen Dar­stellungs­fehler auftreten).
• Zum anderen liegt dieser Wert immer im Bereich zwischen 0 und 1, was die Verwendung von Fix­punkt-Arithmetik nahelegt (siehe Textbox unten).

Die Inter­polations­differenzen (Deltas) ermitteln Sie entlang der Polygon­kanten wie die x-Steigung. Die Horizontal­schritte bleiben für das ganze Polygon konstant, Sie brauchen sie also nur einmal vor dem Zeichnen zu berechnen:

d = ((double)(x0-x2) / 65536.0 *
	(double)(y1-y2) / 65536.0 -
	(double)(x1-x2) / 65536.0 *
	(double)(y0-y2) / 65536.0);
if (d==0.0) return;

id = 1.0 / d;
double y12 = (double)(y1-y2) / 65536.0;
double y02 = (double)(y0-y2) / 65536.0;
dz = ((double)(z0-z2) * y12 - (double)(z1-z2) * y02)*id;
		

Diese Vor­gehens­weise setzt voraus, daß alle Werte als Fix­punkt­zahlen 16:16 vorliegen. Die übrigen Deltas berechnen Sie analog zu dz.

Zum Zeichnen einer Scan­line arbeiten Sie so viele Pixel ab, wie die Linie breit ist. Dabei ändern sich ständig die Werte im Z-Buffer. Ist der aktuelle Pixel drei­dimensional gesehen näher am Betrachter als bisher gezeichnete, oder fehlt an dieser Stelle ein Pixel, setzen Sie ihn mit der angegebenen Farbe.

Abschließend eine einfache Schleife für Polygone mit einheitlicher Farbe:

for (i=0; i<breite ; i++)
{
	if ((z>>16)>zbuffer[i+x1])
	{
		vbuffer[i+x1]=farbe;
		zbuffer[i+x1]=(z>>16);
	}
	// horizontale Werte
	// aktualisieren
	z+=zbuffer_d;
}