Rot-Grün in Bewegung

Carsten Dachsbacher/Nils Pipenbrinck

Spiele warten heutzutage mit faszinierenden 3D-Grafiken auf. Spezielle 3D-Grafikkarten stillen dabei den Leistungs­hunger. Auch in dieser Rubrik haben wir bereits eine einfache 3D-Grafik-Engine entwickelt, die wir nun erweitern (letztes Update in Ausgabe 9/98, ab S. 216). Wenn Sie nicht von Anfang an dabei waren, finden Sie alle bisher erschienenen PC-Underground-Beiträge auf der Heft-CD.

Was genau versteckt sich hinter dem Schlagwort 3D? Im Bereich der Computergrafik bedeutet 3D meist nur, daß die Grafikobjekte durch drei­dimensionale Koordinaten repräsentiert sind. Spätestens für die Ausgabe am Monitor werden die Daten auf die zwei­dimensionale Bildschirm­ebene herunter­projiziert. Die Grafik erscheint somit für jedes Auge gleich. Einen drei­dimensionalen Eindruck suggerieren bestenfalls Bildmerkmale wie die Größe eines bekannten Alltagsgegenstandes: Je kleiner er ist, um so weiter entfernt erscheint er. Ebenso hebt sich auf Portraitfotos der unscharfe Hintergrund von der aufgenommenen Person ab und trägt so zum Eindruck von Tiefe bei.

Um ein virtuelles Objekt räumlich wahrzunehmen, müssen Sie jedem Auge ein eigenes Teilbild präsentieren. Da die Augen bei den meisten Menschen etwa sechseinhalb Zentimeter auseinander liegen, unterscheiden sich die Teilbilder dementsprechend in ihrem Kamerastandpunkt. Wenn Sie beim Betrachten Ihren Kopf zur Seite bewegen, ändert sich Ihr Blickwinkel auf das Objekt nicht – Sie sehen immer noch die gleichen Teilbilder. Daher heißt dieses Verfahren auch „2½D“ oder „Stereo-Sehen“, analog zum Musikgenuß aus zwei Kanälen.

Diesem Manko begegnen Virtual-Reality-Helme und Bewegungssensoren. Damit können Sie Ihren Kopf frei bewegen und sich interaktiv um ein Objekt herumbewegen: 3D par excellence.Ein Computer muß nur die Bewegungsdaten der Sensoren auswerten und die dazu passenden Teilbilder errechnen. Wir beschränken uns in diesem Artikel auf die bereits sehr wirkungsvolle Stereo-Betrachtung.

Rot + Grün = 3D

Da Shutter-Brillen (siehe Textbox auf S. 215) noch zu teuer sind und das Polarisationsverfahren nicht mit Monitoren funktioniert, bietet sich die Rot-Grün-Technik für einen Einbau in das Voxelprogramm (vgl. Ausgabe 1/99, ab S. 244) und die 3D-Engine (vgl. Ausgaben 8/98, ab S. 234 und 9/98, ab S. 216) an. Hierfür berechnen Sie zwei unabhängige Bilder für beide Augen. Da die Echtfarben-Darstellung ohnehin durch die Brille verlorengeht, genügen Graustufen-Bilder. Die zwei Bilder unterscheiden sich in den Positionen der betrachtenden virtuellen Kameras. Sie verwenden also für das linke Bild eine Kamera, die ein wenig nach links von der Betrachterposition verschoben ist, und für das rechte eine Kamera etwas rechts davon.

Um die beiden Bilder für die Ausgabe auf dem Monitor geschickt zusammenzufügen, nutzen Sie die Eigenschaften des im Demosystem verwendeten Farbmodells aus. Mit zwei Shading-Tabellen können Sie die darin enthaltenen Farbwerte so plazieren, daß Sie jeweils nur die Pixel der Einzelbilder mit einem bitweisen Oder verknüpfen müssen, um den endgültigen Farbwert zu erhalten.

Voxelspace umrüsten

Das Voxelprogramm müssen Sie kaum modifizieren. Sie fügen nur einige Zeilen hinzu, um das fertige Programm im Projektverzeichnis VOXEL3D zu erhalten.

Legen Sie statt einer Shading-Tabelle für den Nebeleffekt zwei Tabellen namens fogtable_red und fogtable_green an. Diese enthalten den Rot- und den Grün-Wert für jede Voxel-Farbe und jede Schattierung. Die Berechnung geschieht folgendermaßen:

for(int j = 0; j < 32; j++)
	for(int i = 0; i < 256; i++)
	{
		value = j * j / 32;
		shade = (colormapbmp.cColors
			[i * 4 + 0] * (32 - value)) / 32 +
			(colormapbmp.cColors
			[i * 4 + 1] * (32 - value)) / 32 +
			(colormapbmp.cColors
			[i * 4 + 2] * (32 - value)) / 32;
		shade /= 3;
		fogtable_red[i][j] = ColorCode(shade, 0, 0);
		fogtable_green[i][j] = ColorCode(0, shade, 0);
	}
		

Die Oder-Verknüpfung, mit der Sie zwei Pixel für das endgültige Bild verarbeiten, bauen Sie direkt in die Zeichenroutine des Voxelprogramms ein. Diese einfache Lösung bietet sich an, da jeder Pixel nur ein einziges Mal gezeichnet wird. Sie ändern also in der Prozedur castray nur die Schleife, die die Pixel setzt:

void castray(int col, int horiz,
	int delta_x, int delta_y,
	int fogtable[256][32])
{
	...
	//Schnittpunkt
	if (h>z)
	{
		c=fogtable[colormap8[ofs]][distance >> 3];
		//Diese Schleife wird durchschnittlich 2x durchlaufen
		do
		{
			//Steigung erhöhen
			delta_z += VSCALE;
			//Pixel mit OR setzen
			screen[pixel] |= c;
			//Z erhöhen
			z += ph;
			//in nächsthöhere Bildschirmzeile gehen
			pixel -= SCREEN_X;
			if (pixel < 0) return;
		} while(h>z);
	}
	...
}
		

Wie Sie der geänderten Prozedurdefinition entnehmen, steht Ihnen innerhalb der Prozedur castray die Shading-Tabelle für die Berechnung beider Bilder zur Verfügung. Es fehlt nur noch die neue Schleife, in der Sie die Position der Kamera nach links und rechts versetzen. Den Richtungsvektor für diese Verschiebung berechnen Sie aus der Blickrichtung. Da dieser Vektor zweidimensional ist, erhalten Sie das gewünschte Lot dazu, indem Sie die Komponenten vertauschen und eine davon negieren. Eine neue Schleife ist etwa:

xp = xpos;
yp = ypos;
for(x=0; x < SCREEN_X; x++)
{
	winkel=(BLICKWINKEL * (SCREEN_X - x * 2)) / SCREEN_X;
	delta_x = cos(drehwinkel + winkel) << (RADIX - 16);
	delta_y = sin(drehwinkel + winkel) << (RADIX - 16);

	//bisher:
	//castray(x, neigung, delta_x, delta_y);

	float move = -0.002;
	xpos =xp + move * delta_y;
	ypos =yp - move * delta_x;
	castray(x, neigung, delta_x, delta_y, fogtable_red);

	move = 0.002;
	xpos = xp + move * delta_y;
	ypos = yp - move * delta_x;
	castray(x, neigung, delta_x, delta_y, fogtable_green);
}
		

Der empirisch gewonnene Faktor move bestimmt den idealen Abstand des Betrachters vom Monitor. Damit Sie einen möglichst optimalen 3D-Effekt bekommen, sollten Sie diesen Wert experimentell an Ihren Arbeitsplatz anpassen.

Die Stereo-3D-Engine

Die 3D-Engine der Ausgaben 8/98 (ab S. 234) und 9/98 (ab S. 216) rüsten Sie mit fast ebensowenig Aufwand auf eine echte 3D-Darstellung auf. Im Projektverzeichnis ENGINE3D passen Sie zunächst die Definition der 3D-Objekte so an, daß Sie nicht mehr eine einzige Palette für eine Textur haben, sondern je eine für jedes Teilbild. Entsprechend ändern Sie auch die Textur-Laderoutine LoadTexture(...) im Programmcode der Datei tpolygon.cpp.

Sie verringern die Anzahl der Shading-Abstufungen und der Farbeinträge in diesen Tabellen, indem Sie die Texturfarben nach dem Laden als entsprechende Graustufen behandeln. Der Unterschied fällt nicht auf, da Sie die Bilder in Graustufen berechnen. Zudem sparen Sie etwas Rechenzeit. Passen Sie hierzu die innere Schleife der Polygon-Zeichenroutine an.

Die nächste Änderung nehmen Sie in der Datei 3dclip.cpp vor. Hier erweitern Sie die Prozedur clippolygondraw(...) um einen Zeiger auf die aktuelle Palette. Nach dem Clipping der Polygone gegen das Viewing-Fustrum (das Sichtbarkeits-Volumen) rufen Sie die Polygonroutine auf. Dieser übergeben Sie den Zeiger auf die aktuelle Palette.

Die Methode tobject::draw des Objekts tobject ruft clippolygondraw(...) auf. Fügen Sie dieser Draw-Methode einen zusätzlichen Parameter hinzu, indem Sie das zu zeichnende Teilbild angeben:

void tobject::draw(unsigned short *buffer,
	tcamera *camera, int redgreen)
{
	...
	if (redgreen)
		clippolygondraw(*currentface, *this,
			buffer,palette_green);
	else
		clippolygondraw(*currentface, *this,
			buffer,palette_red);
	...
}
		

Jetzt haben Sie alle Änderungen in den Unterprogrammen erledigt und nehmen sich das Hauptprogramm vor: Bei der 3D-Engine können Sie im Gegensatz zum Voxel nicht beide Bilder gleichzeitig zeichnen, sondern müssen sie unabhängig voneinander bearbeiten. Hierzu definieren Sie einen neuen Speicherbereich für das zweite Bild und eine zusätzliche Kamera.

Alle weiteren notwendigen Änderungen betreffen die Prozedur DrawSzene(...). Berechnen Sie aus der Kameraposition und dem Zielpunkt den Richtungsvektor der Blickrichtung. Das Kreuzprodukt aus diesem Vektor und dem up-Vektor der Kamera ergibt denjenigen Vektor, der vom Betrachter aus nach links zeigt. Damit bestimmen Sie die Verschiebung der beiden Kameras für die zwei Teilbilder. Ein einziger Z-Buffer genügt, da dieser nach dem Zeichnen des ersten Bildes nicht mehr benötigt wird.

Boundary Boxes

Boundary Boxes beschleunigen die Berechnung der 3D-Animation. Es ist schwierig, in 3D-Grafiken sichtbare Polygone so schnell wie möglich von unsichtbaren zu trennen. Wenn Sie ein komplexes 3D-Objekt (oder auch eine Gruppe von Objekten) durch eine sehr einfache Struktur – etwa einen Quader – ersetzen, geht die Berechnung einfach und schnell vonstatten. Prüfen Sie zuerst, ob dieses einfache Objekt in den Sichtbarkeitsbereich der Kamera fällt. Falls nicht, ist auch das darin enthaltene komplexere Objekt nicht sichtbar. Nur bei einem positiven Ergebnis stellen Sie weitere Untersuchungen zur Sichtbarkeit an.

Um die Eigenschaften der objektorientierten Programmierung auszunutzen und den bereits vorhandenen Programmcode zu verwenden, sollten Sie ein Objekt von der Klasse tobject ableiten. Im Beispiel heißt das neue Objekt tboundedobject. Es ist vom Interface her natürlich kompatibel zum alten Objekt. Die folgenden Änderungen finden Sie im Unterverzeichnis ENGINEV2.

Als einfache Repräsentation der Geometrie kommen Objekte wie Kugeln und Quader in Frage. Für eine 3D-Engine, die auf Echtzeit-Berechnung ausgelegt ist, empfehlen sich Quader. Kugeln eignen sich aufgrund der mathematisch einfachen Schnittpunktberechnung mit Geraden eher für Raytracing-Aufgaben.

Berechnen Sie die acht Eckpunkte des Quaders, der das Objekt möglichst eng umschließt. Sie leiten diese direkt aus den Minima und Maxima der Vertex-Koordinaten ab. Die Funktion tboundedobject::calculate_boundarybox() erledigt dies mit einer einfachen Schleife, die jeden Eckpunkt mit den bisherigen Höchst- und Tiefstwerten vergleicht.

Die Funktion sollte direkt nach dem Laden einer 3D-Geometrie ausgeführt werden. Dazu nutzen Sie die Vorzüge objektorientierter Programmierung: Erweitern Sie den vererbten Konstruktor von tboundedobject um den Aufruf von calculate_bondarybox. Dadurch brauchen Sie sich um die Berechnung der Boundary Box nicht zu kümmern.

Die Sichtbarkeit der Box prüfen Sie, indem Sie die acht Eckpunkte der Boundary Box mit dem Sichtbarkeits-Volumen (dem Viewing-Fustrum) der Kamera vergleichen. Dies funktioniert genauso wie das 3D-Clipping.

Dabei testen Sie jeden Punkt einzeln auf den fünf Ebenen des Kamera-Volumens. Diese fünf Ebenen schließen den Bereich im 3D-Raum ein, der von der Kamera aus sichtbar ist. Da Sie einen rechteckigen Bildausschnitt berechnen, handelt es sich um die linke, rechte, obere und untere Kante. Zusätzlich müssen Sie noch gegen die nahe Z-Ebene clippen. Objekte hinter der Kamera sind unsichtbar. Das mathematische Kameramodell, das die 3D-Engine benutzt, erledigt dies nicht automatisch:

unsigned int fustrum_clipcode(const tvector v)
{
	unsigned int clip = 0;
	//znear:
	if (v.z < znear_distance)
		clip |= 1;

	//Links+Rechts
	if (dotproduct(fustrum[0], v) < 0) clip |= 2;
	if (dotproduct(fustrum[1], v) < 0) clip |= 4;

	//Oben+Unten
	if (dotproduct(fustrum[2], v) < 0) clip |=8;
	if (dotproduct(fustrum[3], v) < 0) clip |=16;

	return clip;
}
		

Für jede Ebene, die Sie testen, vergeben Sie ein bestimmtes Bit eines Integers. Die so gewonnenen Bitmuster (Clipcodes) verwenden Sie für die Trivial-Clipping-Methode von Cohen und Sutherland.

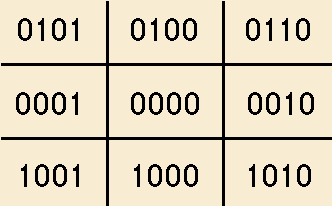
Zunächst betrachten wir den zweidimensionalen Raum: Die Abbildung auf S. 221 oben zeigt alle möglichen Clipcode-Kombinationen. Der Bereich in der Mitte entspricht dem sichtbaren Bildbereich. Bei Punkten links davon ist das unterste Bit gesetzt. Rechts vom Bildbereich wird das zweite Bit gesetzt und so weiter.

Möchten Sie wissen, ob eine Linie (wenigstens teilweise) sichtbar ist, verknüpfen Sie die Clipcodes ihrer beiden Endpunkte mit der Und-Funktion. Ist das Ergebnis ungleich Null, schneidet sie das mittlere Rechteck nicht und ist somit nicht sichtbar. Sonst liegt sie entweder ganz (beide Clipcodes sind dann 0000) oder teilweise im Sichtbarkeitsbereich.

Analog gehen Sie bei 3D-Objekten vor: Sie berechnen zunächst die Clipcodes für alle acht Punkte der Boundary Box. Durch deren logische Verknüpfung erhalten Sie eine Menge Informationen.

Ist die bitweise Und-Verknüpfung aller Punkte ungleich Null, befindet sich die Boundary Box außerhalb des sichtbaren Bereichs. Da die Boundary Box alle Flächen und Eckpunkte unseres Objekts umschließt, muß auch das Objekt selbst unsichtbar sein. Sie können sich daher jede weitere Berechnung sparen und gleich zum nächsten Objekt übergehen. Wird ein Objekt wie hier sofort nach dem Auswerten der Und-Verknüpfung eliminiert, spricht man von einem Trivial Reject Test.

Clipcodes liefern Ihnen noch weitere Informationen. Sind zum Beispiel alle Clipcodes gleich Null, ergibt auch die Oder-Verknüpfung diesen Wert. Das Objekt ist somit vollständig sichtbar, und Sie können das gesamte Clipping überspringen.

Erhalten Sie ein Ergebnis wie 0001, müssen Sie das Objekt nur gegen die linke Ebene clippen. Ähnlich lesen Sie alle anderen Ebenen aus dem kombinierten Clipcode ab. Es ist also sinnvoll, der 3D-Clipping-Funktion den Clipcode des Objektes mitzuliefern. Unser Programmbeispiel läuft mit dieser neuen 3D-Clipping-Funktion etwa doppelt so schnell wie vorher.

Veranschaulichen Sie sich das Kombinieren von Clipcodes einmal auf einem Blatt Papier. Es ist ein hervorragendes Verfahren und kommt in der Computergrafik häufig zum Einsatz. Ob Sie Linien in einer Ebene oder Polygone im drei­dimensionalen Raum betrachten, ist egal. Die zunächst unberücksichtigte Z-Near-Ebene repräsentieren Sie einfach durch ein weiteres Bit. Dabei brauchen Sie für diese Ebene nur die Z-Koordinate eines Eckpunkts zu überprüfen und können auf Skalarprodukte verzichten.

Die Berechnung der Clipcodes und die Behandlung der einzelnen Fälle übernimmt tboundedobject::draw() in der Datei 3dengine.cpp:

void tboundedobject::draw(unsigned short *buffer,
	tcamera *camera)
{
	//Transformationsmatrix des Objektes berechnen
	build_ltm(camera);

	//Boundary Box Test:
	tvector tempvector;
	unsigned int clip_and = 31;
	unsigned int clip_or = 0;
	unsigned int clipcode;

	for(int i = 0; i < 8; i++)
	{
		//Transformation in den 3D-Raum der Kamera:
		transform(boundarybox[i], ltm, tempvector);

		//Clipcode für alle Ebenen berechnen:
		clipcode = fustrum_clipcode(tempvector);

		//Logische Verknüpfungen berechnen:
		clip_and &= clipcode;
		clip_or |= clipcode;
	}

	//Trivial Reject Test:
	if(clip_and) return;
	...
}
		

Partikelsysteme

Computerspiele setzen gern Partikelsysteme ein, um Explosionen, Feuer und andere Phänomene auf den Bildschirm zu zaubern. Diese Systeme zu implementieren ist nicht schwer.

Bei Partikelsystemen werden Objekte nicht mehr durch Polygone, sondern durch einzelne Elemente wie zum Beispiel Punkte dargestellt. Diese einzelnen Teilchen sind ständig in Bewegung. Um starre Körper oder einen Raum zu zeichnen, sind Partikel deshalb ungeeignet. Bei Explosionen, Feuerwerken und dergleichen sind sie Polygon-Objekten hingegen weit überlegen.

Meist genügt eine physikalisch sehr vereinfachte Berechnung der Partikel: Repräsentieren Sie jedes Element durch eine Struktur, die nicht nur dessen Position, sondern auch die Bewegungsrichtung und das „Alter“ speichert:

struct particle
{
	tvector vertice;
	tvector direction;
	long lifetime;
};
		

Das Alter dient dazu, den Partikel nach einiger Zeit wieder verschwinden zu lassen, da Partikeleffekte im relativ beschränkten Raum ablaufen sollen. Als Ausgleich dafür kommen immer wieder neue Teilchen hinzu.

Um einen Partikel darzustellen, zeichnen Sie an der entsprechenden Position im 3D-Raum eine kleine Bitmap additiv auf den Hintergrund. Durch Überlagerung vieler Partikel verwischen die Kanten der Bitmaps, und Sie erhalten den gewünschten Effekt. Von der Lebensdauer des Partikels hängt die Helligkeit der Bitmap ab. Alle Routinen zum Zeichnen von Texturen sind schon in mehreren Helligkeiten vorhanden.

Die Implementation der Darstellung finden Sie in der Datei 3dengine.cpp. Das gesamte Partikelsystem ist als Objekt tparticleobject vom Basisobjekt tobject abgeleitet. Dadurch ersparen Sie sich das erneute Programmieren der 3D-Berechnung und das Laden der Texturen.

Partikel bewegen

Partikel können sich natürlich im 3D-Raum bewegen. Für statische Effekte ist dies überflüssig, Explosionen oder lodernde Feuer verlangen hingegen Mobilität. Durch die Struktur der Partikel bietet sich ein einfaches, an die Physik angelehntes Modell an.

In der Abbildung rechts sehen Sie einen Partikel an seiner alten Position A, seine Richtung als Vektor v sowie seine neue Position B. Die neue Position bestimmen Sie, indem Sie die Richtung v um die Gravitation g verändern. Hierzu addieren Sie einfach die Vektor-Komponenten. Danach verschieben Sie den Partikel um seine neue Geschwindigkeit v’.

So erreichen Sie eine Bewegung, die den physikalischen Tatsachen schon sehr nahe kommt und gut aussieht. Legen Sie noch fest, wie und wo Partikel erzeugt werden. Dafür fassen Sie alle nötigen Informationen in einer Struktur namens particleemitter zusammen:

struct particleemitter
{
	long maxparticles;
	long lifetime;
	long output;
	tvector position_rand;
	tvector speed;
	tvector speed_rand;
	tvector gravity;
};
		

Die Eigenschaft maxparticles legt die maximale Anzahl an Partikeln fest, die ein Partikel-Objekt gleichzeitig verwalten soll. Deren Lebenszeit lifetime wird in berechneten Bildern gemessen. Zusätzlich steuert output, wie viele Partikel pro Bild neu zum Objekt hinzukommen.

Während Sie Partikel generieren, ist es sinnvoll, die Startposition und die Richtung für jeden Partikel etwas zu variieren. Die dafür nötigen Felder sind position_rand und speed_rand. Außerdem legen Sie noch die Grundgeschwindigkeit speed sowie die Gravitationskraft gravity fest.

Auch bei diesem Effekt gilt: Experimentieren lohnt sich. Sie können damit Feuer, Explosionen, Funken und viele andere Lichteffekte nachbilden.

Einzelne Partikel zeichnen

Für die Echtzeit-Grafik ist es sinnvoll, statt einzelner Punkte kleine Bitmaps für die Partikel zu zeichnen. Benutzen Sie deshalb die gleiche Methode (additives Shading) wie für den Lense-Flare-Effekt (vgl. Ausgabe 10/98, ab S. 232).

Setzen Sie die Bildpunkte der Partikel nicht einfach in das Bild ein, sondern „addieren“ Sie sie auf die aktuellen Pixelwerte. Dadurch verwischen die Kanten zwischen den Partikeln, und Sie benötigen wesentlich weniger einzelne Teilchen.

Wenn Sie mit dem addierenden Zeichnen nicht vertraut sind, stellen Sie sich mehrere Dia-Projektoren vor, mit denen Sie verschiedene Bilder auf eine Leinwand projizieren. Je mehr Bilder Sie übereinander legen, desto heller werden die Pixel an den überlagerten Stellen. Das additive Zeichnen kostet zwar viel Zeit, aber da Sie für einen realistischen Effekt wesentlich weniger Partikel brauchen, schneiden Sie im Zeitvergleich besser ab.

Die Partikel zeichnen Sie immer erst am Schluß, da Sie keine Z-Buffer-Werte für die Partikel besitzen. Der Z-Buffer enthält nach dem Zeichnen der Objekte immer den minimalen Abstand zum Betrachter für einen Pixel. Außerdem kennen Sie zu jedem Partikel dessen Abstand zum Betrachter.

Vor dem Zeichnen vergleichen Sie einfach diesen Wert mit dem Z-Buffer-Wert des Bildes an der Stelle, an welcher der Partikel im zweidimensionalen Raum sitzt. Ist er näher als ein dort gezeichnetes Polygon, zeichnen Sie ihn auch dort. Andernfalls ist er nicht sichtbar. Beachten Sie aber, daß Sie den Z-Buffer keinesfalls ändern dürfen, sonst könnte ein vorne liegender Partikel einen hinteren überdecken. Das darf nicht passieren, da alle Partikel transparent sind.

Solche Partikel­objekte können Sie auch mit Polygon­objekten kombinieren, um etwa die Triebwerke eines Raumschiffs mit einer Partikelflamme auszustatten. Die vorge­nommenen Erweiterungen der 3D-Engine bieten interessante Ansätze, mit denen Sie weiter­experimentieren können.