Tanz der Pixel

Carsten Dachsbacher

Nachdem Sie in der letzten Ausgabe von PC Underground einiges über Sounds gelernt haben, dreht sich diesmal alles um die Grafik. Für unser Projekt eines Weltraum-Ballerspiels spielt dabei die Animation der fliegenden Raumgleiter eine wichtige Rolle. Diese Aufgabe bewältigen Sie am besten mit sogenannten Sprites.

Sprites sind kleine, auf dem Bildschirm frei bewegliche Grafiken, die auch durchsichtige Stellen aufweisen können. Sie tauchen nicht nur in vielen Spielen auf – das wohl bekannteste Beispiel eines Sprite ist sicherlich Ihr Mauszeiger. Sogar auf Web-Seiten kommen heute Sprites zum Einsatz: Dank der Layer-Technik können Sie Grafiken schrittweise an immer neuer Stelle plazieren.

Bereits so betagte Heimcomputer wie der Commodore 64, der Amiga sowie der Atari haben eine Hardware-Unterstützung für Sprites zur Verfügung gestellt. Auch die meisten Spielekonsolen bieten diese heute an. Dies spart Rechenzeit und vereinfacht den Umgang mit bewegten Objekten. Auf dem PC allerdings mußten sich Programmierer schon immer selbst um alles kümmern. Dabei will die Darstellung, Bewegung und eventuell das Wieder­herstellen des Bildschirm­inhalts beim Weiter­bewegen eines Sprite geschickt implementiert sein.

Sprites verwalten

Um ein Sprite zu speichern und anzuzeigen, gibt es eine einfache Methode: Sie merken sich dessen Breite und Höhe und reservieren einen entsprechend großen Speicher­bereich für die Bilddaten. Das sieht dann folgendermaßen aus:

typedef struct
{
	int size_x, size_y; // Größe
	// Zeiger auf Daten
	short *data;
}
		

Die Größe des Speicher­bereichs beträgt Breite mal Höhe mal Speicher­verbrauch eines Pixels (in unserem Fall 2 Byte).

Für durchsichtige Stellen des Sprite legen Sie einen gewöhnlichen Farbcode fest, den Sie entbehren können. Der Code mit dem Wert 0 eignet sich dafür hervorragend, weil Sie ihn in Assemblercode besonders schnell abfragen können. Zwei verschachtelte Schleifen, je eine für die Höhe und die Breite, zeichnen das Sprite auf den Monitor:

for(int y = 0; y < size_y; y++)
	for(int x = 0; x < size_x; x++)
	{
		short farbcode = data[x + y * size_x];
		if(farbcode!=0)
		 Bildschirm[x + pos_x + (y + pos_y) * SCREEN_X] = farbcode;
	}
		

Wie Sie sehen, müssen Sie mit dieser Methode immer alle Pixel des Sprite auslesen und auf Gleichheit mit Null prüfen, egal wie viele Pixel gesetzt sind. An dieser Stelle ahnen Sie sicher schon, daß es ein eleganteres Verfahren gibt.

Die folgende Vorgehensweise nutzt eine Idee aus der Daten­komprimierung, die sogenannte Lauflängen­codierung (Runlength Encoding, RLE). In der einfachsten Version, wie sie zum Beispiel Bestandteil mancher Grafikformate ist, ersetzt der Algorithmus aufeinander­folgende, gleichfarbige Pixel durch die Anzahl und deren Farbwert. Bei einem einfachen Testszenario erhalten Sie aus 1,1,1,1,2,2,3,3,3,4,5,5 folgende Ausgabe: 4,1,2,2,3,3,1,4,2,5 Wie Sie der Ausgabe entnehmen, bestand die Eingabe aus vier Einsern, ge folgt von zwei Zweiern, drei Dreiern, einem Vierer und zwei Fünfern. Bei einem häufigen Wechsel der Eingabewerte nimmt die Datenmenge jedoch nicht sehr ab. In diesem Beispiel spart das Verfahren gerade mal zwei Werte ein.

Beim Entpacken gehen Sie umgekehrt vor: Zuerst lesen Sie die Anzahl aus, dann den Wert, den Sie entsprechend oft kopieren.

Eben das nutzen Sie für Ihre Sprites. Dazu unterscheiden Sie zwischen durchsichtigen (Farbwert gleich 0) und undurch­sichtigen (Farbwert ungleich 0) Pixeln des Sprite. Beim Codieren des Sprite zählen Sie dann innerhalb einer Zeile die Anzahl der zusammen­hängenden Pixel. Diese Anzahl speichern Sie und lassen bei undurch­sichtigen Bereichen die Pixeldaten folgen.

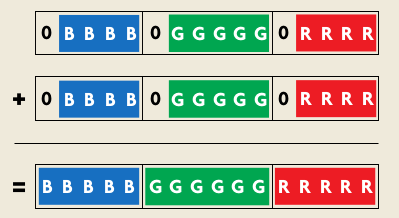
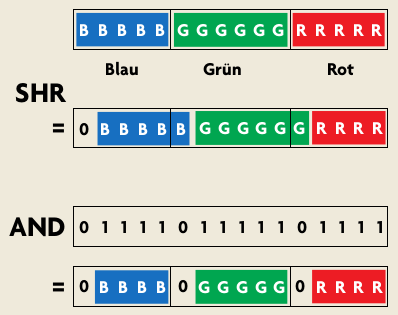
Nun fehlt Ihnen noch der Hinweis, ob sich die Mengenangabe auf einen durchoder undurch­sichtigen Teil bezieht. Da Sie die Sprite-Daten als 16-Bit-Werte vorliegen haben, können Sie zur Charakter­isierung das höchstwertige Bit (Most Significant Bit, MSB), verwenden. Sie setzen das MSB in einem 16-Bit-Wert durch eine bitweise Oder -Verknüpfung mit dem Wert 32768.

Als Beispiel hier die Codierung einer Sprite-Zeile. Eine Datenreihe wie: 0,0,0,0,1,2,3,4,0,5,6 ergibt codiert: 4 or MSB,4,1,2,3,4,1 or MSB,2,5,6 Der Vorteil dieser Methode ist, daß das Decodieren praktisch keine Zeit kostet und Sie nur die Sprite-Daten lesen müssen, die undurch­sichtige Pixel enthalten. Ein Vergleich mit dem Wert 0 entfällt komplett. Am Ende einer Sprite-Zeile signalisieren Sie noch mit einem festgelegten Code, daß die Zeichenroutine in die nächste Bildschirm­zeile springen muß.

Natürlich könnten Sie am Ende einen durchsichtigen Bereich ins Sprite einfügen, der so groß ist, daß der Zeiger auf die Bildschirm­daten danach an der richtigen Stelle steht. Dieser Bereich wäre so groß wie die Breite des Monitors minus der Breite des Sprite.

Dieser Ansatz bringt aber zwei entscheidende Nachteile mit sich: Zum einen sind die so generierten Sprite-Daten dann nicht mehr unabhängig von der Auflösung des Bildschirms. Zum anderen erfordert es zusätzlichen Aufwand beim Clipping (Abschneiden) der Sprites am Bildschirmrand.

Daher empfiehlt sich eine spezielle Zeilenende-Markierung. Als Escape-Code für den Zeilensprung eignet sich zum Beispiel der Wert 65535. Diesen Code bräuchten Sie nur bei 65535 minus 32768 durchsichtigen Pixeln in einer Sprite-Zeile – doch dieser Fall dürfte kaum jemals eintreten.

Als zusätzliche Information speichern Sie noch die Größe sprite.size des codierten Sprite. Die genaue Codierungs­routine entnehmen Sie dem Quellcode zu diesem Artikel, den Sie wie immer auf der Heft-CD sowie im Internet-Angebot des PC Magazin finden.

Sprites zeichnen

Ein solchermaßen codiertes Sprite zeichnen Sie nun relativ schnell:

int spriteoffset=0;
short* adresse = x_pos + y_pos * SCREEN_X;
while(spriteoffset < sprite.size)
{
	// Wert auslesen
	data = sprite.data[spriteoffset++];
	if(data == NEWLINE)
	{
		// Code für neue Zeile
		adresse += SCREEN_X - sprite.size_x;
	} else
	if(data & MSB)
	{
		// MSB gesetzt => Transparente Stelle
		adresse += data - (unsigned int)MSB;
	} else
	{
		// Undurchsichtige Stelle => „data“ Pixel kopieren
		for(unsigned int i = 0; i < data; i++)
			*adresse++ = sprite.data[spriteoffset++];
	}
}
		

Zu dieser Routine finden Sie im Source-Code auch eine optimierte Assembler-Version, die noch etwas schneller arbeitet.

Jetzt bleibt Ihnen noch die Aufgabe, das Clipping zu lösen, also das Abschneiden der Teile eines Sprite, die nicht auf den Bildschirm passen. Das Clipping an der oberen und unteren Kante gestaltet sich relativ leicht: Ragt ein Sprite oben über den Anzeigebereich hinaus, lassen Sie entsprechend viele Sprite-Zeilen aus.

In der Praxis lesen Sie die Sprite-Daten aus und zählen die Anzahl der Codes, die einen Zeilenwechsel anzeigen. Achten Sie bei dieser Routine nur darauf, daß Sie dabei die Pixel-Daten überspringen und nicht als Steuercodes interpretieren.

Eine sehr elegante und etwas schnellere Methode bedient sich einer Sprungtabelle zu jedem Sprite, in der für jede Zeile der Index auf die Sprite-Daten vermerkt ist. Wenn Sie etwa drei Zeilen überspringen möchten (Zeile 0 bis 2), und Zeile 3 bei Index 100 beginnt, stünde in der Tabelle der Eintrag 100.

Das Clipping an der unteren Kante gestaltet sich noch einfacher: Sie verwenden eine Variable, die Sie mit der y-Start­koordinaten des Sprite initialisieren. Immer wenn Sie eine neue Sprite-Zeile anspringen, erhöhen Sie diesen Wert. Erreicht die Variable einen Wert größer oder gleich der Anzahl der Bildschirm­zeilen, beenden Sie das Zeichnen.

Das Clipping an den Seiten funktioniert prinzipiell genauso wie an den anderen Kanten: Sie fügen jeweils Zähler ein, wie viele Pixel Sie noch auslassen (linke Kante) bzw. nach wie vielen Pixeln Sie zu zeichnen aufhören (rechte Kante). Natürlich müssen Sie dabei auch die unsichtbaren Pixel auslesen.

Sprites generieren

Damit haben Sie alle Routinen, um einen Sprite zu zeichnen. Ihnen fehlen nur noch die Sprite-Daten selbst. Raumschiffe, wie Sie sie im Beispiel­programm sehen, fertigen Sie mit jedem beliebigen Zeichen- oder 3D-Modeling-Programm an. Möchten Sie nicht mit Microsoft Paint aus dem Windows-Zubehör arbeiten, können Sie zum Beispiel das Shareware-Programm Paintshop Pro von der Heft-CD benutzen.

Um den Arbeitsaufwand zu vermindern, zeichnen Sie jedes Bild des Raumschiffs nur für eine Flugrichtung. Für alle anderen Richtungen lassen Sie sich die entsprechenden Sprites berechnen. Ein gedrehtes Sprite erhalten Sie bereits mit wenigen Zeilen Quelltext.

Zuerst berechnen Sie zu jedem Pixel an der Stelle x/y des gedrehten Sprite den zugehörigen Vektor vom Sprite-Mittelpunkt aus:

for(int y = 0; y < spritehoehe; y++)
	for(int x = 0; x < spritebreite; x++)
	{
		vektor.x = x - spritebreite / 2;
		vektor.y = y - spritehoehe / 2;
	}
		

Nach einer Rotation dieses Vektors sehen Sie dann, auf welches Pixel er im ursprünglichen Sprite zeigt. Dieses Originalpixel setzen Sie an die Position x/y des neuen Sprite.

Durch solche Drehungen entstehen im berechneten Bild meist unschöne Anomalien. Schuld daran ist das Abschneiden der Nachkomma­stellen bei der Konvertierung der Koordinaten zurück in Ganzzahlwerte. Wenn Sie die entsprechenden Nachkomma­anteile berück­sichtigen, erhalten Sie deutlich schönere Ergebnisse.

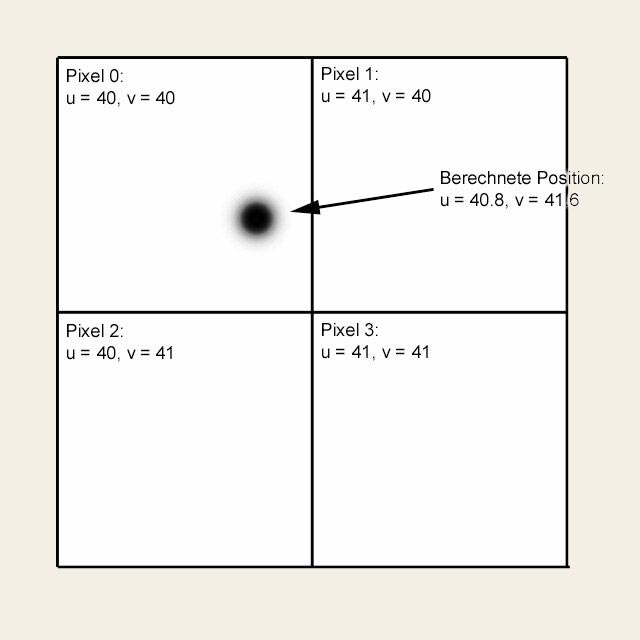
Dazu bedienen Sie sich der bilinearen Interpolation. Betrachten Sie einmal das Bild auf Seite 227: Die berechnete Position 40,8/40,6 ergibt ohne Beachtung der Nachkomma­stellen das Pixel 0 links oben, obwohl sie schon sehr nahe an der der anderen Pixel liegt.

Bei der bilinearen Interpolation vertuschen Sie diesen Fehler durch eine gewichtete Farbgebung. Dabei berück­sichtigen Sie für jede Position die relative Lage zu den vier umliegenden Pixeln. Den idealen Farbwert erhalten Sie, indem Sie für jede Farbkomponente – hier am Beispiel Rot mit den aktuellen Positions­werten gezeigt – wie folgt vorgehen:

Rot_oben = (1.0 - 0.8) * Rot_Pixel0 + 0.8 * Rot_Pixel1
Rot_unten = (1.0 - 0.8) * Rot_Pixel2 + 0.8 * Rot_Pixel3
Rot_gesamt = (1.0 - 0.6) * Rot_oben + 0.6 * Rot_unten
		

Sie lesen also die umgebenden Pixel und deren Farb­komponenten aus und berechnen mit Hilfe der Nachkomma­stellen die gewichteten Farbanteile. Die so gewonnene neue Farbe verwenden Sie für das Pixel an der Zielposition (in unserem Beispiel Pixel 0).

Warum Sie damit, zum Beispiel bei einer Vergößerung, einen besseren optischen Effekt erzielen, ist einleuchtend: Statt grober Pixel sehen Sie fein abgestufte Farbnuancen. Bei einer Drehung können Sie sich vorstellen, daß ein Pixel nichts anderes ist als ein kleines Quadrat. Beträgt der Drehwinkel etwa 45 Grad, so liegt dieses Quadrat nicht vollständig deckend auf einem Pixel, sondern bedeckt mehrere davon – diese aber nur teilweise. Im Sourcecode finden Sie eine Routine, die Ihnen die Berechnung der Drehschritte abnimmt:

CreateRotationAnimation(SPRITE *sprite, int steps, bitmaptype bmp)
		

Dieser Funktion übergeben Sie eine Liste von Sprite-Strukturen, die Anzahl der Drehschritte (steps) sowie eine bitmaptype -Struktur. In letztere laden Sie zuvor mit bmp_load(...) eine quadratische Bitmap. Beachten Sie beim Entwurf der Sprites, daß die Farbe 0, also Schwarz, als transparent interpretiert wird.

Partikelsysteme

Für die Darstellung von Explosionen und aufsteigenden Rauch könnten Sie ebenfalls Sprites einsetzen. Eleganter und effizienter programmieren Sie diese Effekte aber mit einem Partikelsystem. Auch wenn Sie PC Underground schon länger verfolgen und die Partikel­effekte aus der 3D-Engine in Ausgabe 2/99 kennen, sollten Sie weiterlesen. Diesmal lernen Sie noch effizientere Methoden zur Partikel­verwaltung und eine elegante Steuerung der Partikel-Emitter kennen.

In unserem Fall ist ein Partikel nichts anderes als ein kleiner, 4 x 4 Pixel großer Punkt, dessen Helligkeit auf das aktuelle Bild addiert wird. Wie Sie dies elegant im HiColor-Farbraum erledigen, lesen Sie in der Textbox „Halbt­ransparenz und additives Shading in HiColor“ auf S. 231.

Jedes dieser Partikel besitzt eine aktuelle Position, eine Bewegungs­richtung und einen Beschleunigungs­vektor. Für diese Werte genügen natürlich keine ganzzahligen Werte, Sie brauchen Kommazahlen. Eine schnelle Lösung bieten Fixpunktzahlen mit je 16 Bit für die Vorund Nachkomma­stelle (siehe Textbox „Fixpunkt-Arithmetik“ auf S. 229).

Zusätzlich erhält jedes Partikel noch eine Lebensdauer, anhand derer Sie zum Beispiel dessen aktuelle Farbe berechnen. Dieser Wert dient außerdem dazu, ein Partikel nach einer bestimmten Zeitdauer wieder verschwinden zu lassen.

Ein Partikel besitzt also folgende Eigenschaften:

typedef struct
{
	int life; // Lebensdauer
	int x, y; // Position
	int dx, dy; // Bewegung
	int ddx, ddy; // Beschleunigung
} PARTICLE;
		

Von dieser Struktur legen Sie eine ganze Reihe an, in unserem Fall 10 000 Partikel. Für eine schöne Raumschiff­explosion brauchen Sie davon ca. 5000:

#define MAXPARTICLES 10000

PARTICLE particle[MAXPARTICLES];
		

Um eine Explosion darzustellen, initialisieren Sie genügend Partikel­strukturen und erwecken diese zum Leben. Dazu müssen Sie aber erst herausfinden, welche der Einträge in particle noch nicht belegt sind. Eine Methode wäre: Sie suchen alle Einträge durch, bis Sie genügend freie gefunden haben. Bei 10 000 Partikeln kostet das allerdings zu viel Rechenzeit.

Deshalb verwalten Sie die freien Partikel in einem Stapel (Stack): Legen Sie dazu eine Liste an, die genauso viele Integer-Werte aufnehmen kann wie die maximale Zahl der Partikel. Auf das obere Ende des Stapels zeigt ein spezieller Zeiger, der sogenannte Stackpointer. Die Initialisierung nehmen Sie wie folgt vor:

int free_particle[MAXPARTICLES];
int index_free;

for(i = 0; i < MAXPARTICLES; i++)
	free_particle[i]=i;

index_free = MAXPARTICLES;
		

In dieser Liste stehen alle Partikel­indizes, deren Struktur frei ist – am Anfang eben alle. Jedesmal, wenn Sie ein Partikel benutzen, holen Sie sich die Nummer eines freien Partikels und entnehmen ihn aus der Liste (ein sogenannter Pop vom Stack):

// keiner frei
if(index_free <= 0) return;

nummer = free_particle[–index_free];
		

„Stirbt“ ein Partikel, das heißt, verläßt es den Bildschirm oder ist seine Lebensdauer abgelaufen, schreiben Sie seine Nummer wieder in die Liste (entspricht einem Push auf den Stack):

free_particle[index_free++] = nummer;
		

Somit erhalten Sie immer Zugriff auf freie Strukturen, ohne nach ihnen suchen zu müssen.

Jetzt, da Sie eine freie Struktur gefunden haben, füllen Sie sie aus. Werte für eine Explosion an der Stelle x/y sehen beispielsweise so aus:

void AddExplosion(int x, int y, int anzahl)
{
	for(int d = 0; d < anzahl; d++)
	{
		if(index_free <= 0) return;
		int n = free_particle[–index_free];

		float richtung1 = rand() / 32768.0f * PI_2;
		float speed1 = rand() / 32768.0f * 0.5f;
		float richtung2 = rand() / 32768.0f * PI_2;
		float speed2 = rand() / 32768.0f * 0.01f;

		// Position, durch Zufallswerte leicht verschoben
		particle[n].x =(x << 16) + (rand() - 16384) * 32;
		particle[n].y =(y << 16) + (rand() - 16384) * 32;
		// Geschwindigkeit
		particle[n].dx = sin(richtung1) * speed1 * 65536.0f;
		particle[n].dy = cos(richtung1) * speed1 * 65536.0f;
		particle[n].ddx = sin(richtung2) * speed2 * 65536.0f;
		particle[n].ddy = cos(richtung2) * speed2 * 65536.0f;
		particle[n].life = (128 + (rand() / 32768.0f * 16.0f)) << 16;
	}
}
		

Nun lassen Sie die Partikel über den Bildschirm fliegen. Dabei sollten Sie eine gleichmäßig schnelle Bewegung der Partikel unabhängig von der Geschwindig­keit des Rechners gewährleisten. Berechnen Sie dazu die Zeitdifferenz zwischen der letzten Bewegung eines Partikels und der aktuellen Zeit, und skalieren Sie die Geschwindig­keit und die Beschleunigung entsprechend:

// Skalierung
step = (65536.0f * (zeit - alte_zeit) / 20.0f);

for(i=0; i < MAXPARTICLES; i++)
	if(particle[i].life > 0)
	{
		int dead = 0;
		particle[i].x += imul16(particle[i].dx, step);
		particle[i].y += imul16(particle[i].dy, step);
		particle[i].dx += imul16(particle[i].ddx, step);
		particle[i].dy += imul16(particle[i].ddy, step);
		int x = particle[i].x >> 16;
		int y = particle[i].y >> 16;

		// Bildschirm verlassen?
		if(x >= SCREEN_X - 6)
			dead = 1;
		else if (x < 0)
			dead = 1;
		if( y >= SCREEN_Y - 6)
			dead = 1;
		else if (y < 0)
			dead = 1;

		explosion_particle[i].life -= imul16(65536, step);

		// Lebensdauer abgelaufen?
		if(explosion_particle[i].life <= 0) dead = 1;
		if(dead)
			// Partikel freigeben
		else
			// Partikel zeichnen
	}
		

Die Funktion imul16 ist hier die Multiplikations­routine für Fixpunktzahlen.

Das Partikel zeichnen Sie nun, indem Sie die Farbe aus der Lebensdauer berechnen und additiv einen kleinen Kasten an seiner Position setzen:

// Farbwert berechnen und gleich Bitmaske anwenden
life = explosion_particle[i].life >> 17;
r = g = b = 16;

if(life > 48)
	b += life - 48
else
	b += life / 4;

if(life > 32)
	g += life - 16
else
	g += life / 2;

r += life;
farbe=ColorCode(r, g, b) & mask;

adress = screen + (x + y * SCREEN_X);
for(int b=0; b < 4; b++)
{
	for(int a = 0; a < 4; a++)
	{
		int back = *adress;
		back &= mask;
		*adress = remappalette[(farbe + back) > 1];
		adress++;
	}
	adress += SCREEN_X - 4;
}
		

Die Zeichenroutine, die Sie im Quelltext auf der Heft-CD finden, enthält zusätzlich wieder eine Assembler-Version, die die Pixel an den Partikelecken abdunkelt. Dadurch erhalten Sie runder wirkende Partikel, die etwas schöner aussehen.

Nun besitzen Sie das Handwerkszeug, um Partikel­explosionen zu generieren. Es fehlt Ihnen aber noch ein eleganter Weg, größere zusammen­gesetzte Explosionen bequem zu erzeugen. Dazu bedienen Sie sich des Prinzips einer Warteschleife:

#define MAXQUEUE 32
typedef struct
{
	// Position, Dichte, Typ, Flag
	int x,y,density,type,used;
	// Zeitangabe für Explosion
	int time;
} EXPLOSION_QUEUE;

EXPLOSION_QUEUE queue[MAXQUEUE];
		

Wenn Sie eine zusammen­gesetzte Explosion starten wollen, suchen Sie sich einen freien Eintrag in der Liste und tragen Ihre Wunschdaten ein. Die Variablen bestimmen die Position der Explosion, die Dichte (also die Anzahl der Partikel) sowie den Typus, falls Sie verschiedene Typen implementiert haben:

int i = 0;
while((i < MAXQUEUE) && (explosion_queue[i].used))
	i++;

// Warteschlange voll
if(i == MAXQUEUE) return;

queue[i].used = 1;
queue[i].x = Position x;
queue[i].y = Position y;
queue[i].density = 400;
queue[i].type = 0;
queue[i].time = GetDemoTime() + 250;
		

Dieses Beispiel initialisiert eine Explosion, die 250 Millisekunden später beginnt. Die Funktion HandleExplosion() arbeitet nun die Warteschlange ab:

void HandleExplosion()
{
	int time = GetDemoTime();

	for(int i = 0; i < MAXQUEUE; i++)
	if((explosion_queue[i].used)
		&& (explosion_queue[i].time <= time))
	{
		explosion_queue[i].used = 0;
		AddExplosion(
			explosion_queue[i].x,
			explosion_queue[i].y,
			explosion_queue[i].
			density);
	}
}
		

Die Routine rufen Sie bei jedem Bildschirm­aufbau auf, die Explosionen starten dann wie gewünscht. Den optischen Eindruck einer solchen Explosion sehen Sie im Bild auf S. 230.

Den Feuerstrahl am Antrieb des Raumschiffs haben wir übrigens auch mit dem Partikelsystem berechnet und dann dem Sprite des Raumgleiters hinzugefügt. Im Sourcecode finden Sie neben der Explosions­routine noch analoge Funktionen für Rauch- und Flammeneffekte.

An dieser Stelle haben Sie schon fast alle Grundlagen geschaffen, die Sie für das Programmieren des Spiels benötigen. In der nächsten Ausgabe lernen Sie noch die Algorithmen zur Abfrage von Sprite-Kollisionen kennen, bevor Sie sich dann ganz dem Hauptteil des Spiels widmen.