Lifting für Logos

Carsten Dachsbacher

Nach der Spiele­programmierung der letzten Ausgaben liegt der Schwerpunkt dieser Ausgabe wieder bei den klassischen Demos. Sie werden als Designer tätig und gestalten professionelle Grafiklogos. Dazu lernen Sie verschiedene Effekte kennen, mit denen Sie diese Logos eindrucksvoll in Szene setzen. In diesem Zusammenhang steigen Sie in die Assembler-Programmierung mit MMX-Befehlen ein.

Licht-Logo

Vielleicht kennen Sie die Logos am Anfang einiger Computerspiele, die den beleuchteten Schriftzug des Herstellers zeigen. Mit einem solchen Effekt beginnen Sie Ihre Tätigkeit als Logo-Designer. Dabei soll sich eine Lichtquelle hinter einem Schriftsatz, einem Bild oder einem sonstwie gestalteten Logo hin- und herbewegen.

Das allein wäre allerdings unspektakulär. Deshalb soll diese Lichtquelle sichtbare Lichtstrahlen aussenden, die je nach Strahlungs­richtung durch die durchsichtigen Stellen des Logos hindurch­scheinen bzw. an den undurch­sichtigen Stellen absorbiert werden (siehe Bild unten).

Den angesprochene Effekt können Sie relativ leicht in 3D programmieren. Auf der Skizze auf S. 220 erkennen Sie ein zwei­dimensionales Logo, das auf der x/y-Ebene steht. Die Lichtquelle befindet sich im Halbraum der positiven z-Achse (also in dem Teil des Raums mit positiven z-Koordinaten). Der Betrachter steht gegenüber auf der negativen z-Achse.

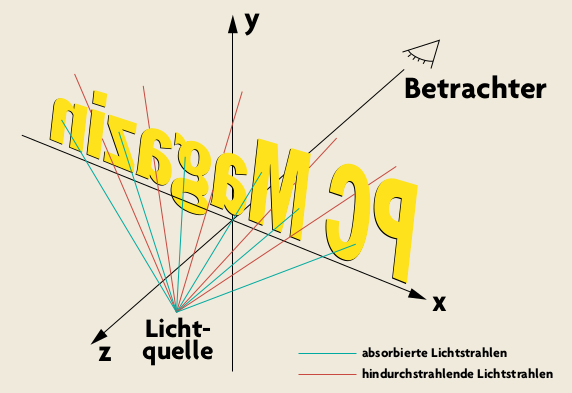
Anhand dieser Vorstellung können Sie das Problem wie folgt beschreiben: Vorgegeben sind die Position der Lichtquelle und die Richtung eines Lichtstrahls. Eine Position und eine Richtung definiert eine Halbgerade, deren Schnittpunkt mit der x/y-Ebene Sie berechnen können. Befindet sich an dieser Stelle ein Pixel des Logos, endet der Lichtstrahl an dieser undurch­sichtigen Stelle. Sonst setzt das Licht seinen Weg fort, und der Strahl ist vor dem Logo zu sehen. Mit Hilfe der Schnittpunkte stellen Sie nicht nur fest, ob der Strahl absorbiert wird oder nicht. Sie dienen auch dazu, einen Lichtstrahl in den hinter dem Logo befindlichen Teil und den eventuell vorhandenen Teil davor aufzuteilen.

Damit die Lichtstrahlen nicht unnatürlich wirken, weisen Sie ihnen zu Beginn per Zufalls­generator eine zufällige Länge zu. Diese Längenangaben fließen dann in die Richtungs­vektoren der einzelnen Strahlen ein. Die Farbe der Lichtstrahlen erhalten Sie aus ihrer Richtung und einer zufälligen Abweichung.

Im mathematischen Fachjargon formulieren Sie die bisherigen Überlegungen wie folgt:

Position der Lichtquelle:
	(lx, ly, lz)
Richtung des Strahls:
	(rx, ry, rz)
Schnittpunkt:
	(sx, sy, sz)
		

Den Schnittpunkt des Strahls mit der x/y-Ebene berechnen Sie nun ganz einfach:

t = 0.0 - lz / rz;
sx = lx + t * rx;
sy = ly + t * ry;
// sz = 0.0, da Schnittpunkt
// mit xy-Ebene
sz = 0.0;
		

Interessant für die Schnittpunkte sind nur die Geraden­gleichungen, bei denen der Wert t größer als 0 ist: Bei einem negativen Wert t würden die Halbgeraden vom Betrachter wegzeigen und könnten deshalb keinen Schnittpunkt mit der x/y-Ebene besitzen.

Außerdem müssen Sie darauf achten, daß der Lichtstrahl nur eine gewisse Länge besitzt. Wenn Sie den Schnittpunkt der Ebene mit der Halbgeraden eines Lichtstrahls berechnen, darf der Schnittpunkt nicht weiter entfernt sein, als der Lichtstrahl lang ist. Schneidet ein Lichtstrahl die x/y-Ebene gar nicht, liegt der Strahl vollständig hinter dem Logo.

An dieser Stelle haben Sie entweder festgestellt, daß ein Lichtstrahl keinen Schnittpunkt mit der x/y-Ebene hat, oder Sie haben diesen berechnet. Das wiederum bedeutet, daß Sie nun einen (Teil-) Strahl kennen, der eindeutig hinter dem Logo liegt: Der Strahl von (lx, ly, lz) nach (sx, sy, sz). Alle Strahlen, die Sie so bestimmt haben, speichern Sie in einer Liste. Mit ihrer Hilfe zeichnen Sie später die Strahlen auf den Bildschirm.

Mit sx und sy können Sie die Koordinaten des Pixels im Logo berechnen, der am Schnittpunkt liegt. Dazu addieren Sie die halbe Bildschirm­breite und -höhe, wenn Sie die Mitte des Logos im Ursprung des Koordinaten­systems annehmen:

int x = SCREEN_X / 2 + sx;
int y = SCREEN_Y / 2 + sy;
		

Nun überprüfen Sie noch, ob an dieser Stelle ein Pixel gesetzt ist oder die Koordinaten auf eine Position innerhalb der Logo-Bitmap zeigen. Bei folgenden Berechnungen verwenden Sie eine Logo-Bitmap, die die gleichen Ausmaße wie die Bildschirm­auflösung aufweist (also eine Breite von SCREEN_X und eine Höhe von SCREEN_Y Pixel):

if(((ix>=0) &&
	(ix <= SCREEN_X) &&
	(iy >= 0) &&
	(iy <= SCREEN_Y)) &&
	(logo[ix + iy * SCREEN_X] == 0))
{
	// Vorderen Teil des Strahls berechnen
	...
}
		

Von dem Teil des Lichtstrahls, der sich vor dem Logo befindet, kennen Sie den Start- und Endpunkt: Er beginnt am Schnittpunkt des Strahls mit der Ebene und endet in dem Punkt, den Sie durch Addition des Richtungs­vektors des Strahls mit dem Ortsvektor der Lichtquelle erhalten. Auch diese Information speichern Sie zunächst in einer Liste.

Lichtstrahlen zeichnen

Da sich der Betrachter immer auf der negativen z-Achse befindet, können Sie die drei­dimensionalen Koordinaten mit einer einfachen Perspektiv­transformation in zwei­dimensionale Bildschirm­koordinaten umrechnen. Dies geschieht mit der folgenden Formel, wobei v3d der drei­dimensionale und v2d analog dazu der zwei­dimensionale Vektor ist. Als Koordinaten­system liegt hierbei jeweils die Bildschirm­ebene zugrunde:

// 1000.0f ist empirisch
// ermittelter Projektionsfaktor
inverse_z = 1000.0f / (v3d.z + 1000.0f);
v2d.x = v3d.x * inverse_z + SCREEN_ X / 2;
v2d.y = v3d.y * inverse_z + SCREEN_ Y / 2;
		

Mit dieser Formel projizieren Sie alle berechneten Lichtstrahlen auf die Betrachter­ebene, also auf den Bildschirm. Mit den so gewonnenen Koordinaten können Sie die Lichtstrahlen einfach als Geraden auf den Bildschirm bringen. Zuerst zeichnen Sie alle Linien­abschnitte, die hinter dem Logo liegen. Danach stellen Sie das Logo selbst dar und zu guter Letzt die vor dem Logo liegenden Strahlen.

Um eine Linie zu zeichnen, gibt es viele Ansätze, doch genügt ein relativ einfacher Algorithmus. Damit die Linien über den Bildschirmrand hinausgehen können, müssen Sie sie vorher abschneiden (sogenanntes Clipping).

Clipping

Das Clipping von Linien scheint ein Lieblingsthema der Forscher auf dem Gebiet der 3D-Grafik zu sein. Entsprechend viele Algorithmen gibt es auch. Optimal geeignet ist der Algorithmus im Programm LightLogo.cpp, das Sie komplett auf der Heft-CD finden.

So gehen Sie vor: Sie teilen die Betrachter­ebene in neun verschiedene Gebiete ein. In der Mitte befindet sich der rechteckige Bildschirm­bereich, umgeben von den unsichtbaren Bereichen. Diese befinden sich in Relation zum sichtbaren Bild links oben, oben, rechts oben, links, rechts, links unten, unten sowie rechts unten. Der Algorithmus prüft, in welchem dieser Bereiche eine Linie endet, sofern sie über den Rand hinausgeht. Für jeden einzelnen Fall stellt der Algorithmus einen speziell angepaßten Code zur Verfügung. Dies erhöht die Codegröße deutlich, birgt aber einen großen Geschwindigkeits­vorteil.

Um an dieser Stelle nicht zu weit in – für den eigentlichen Effekt eher nebensächliche – Details zu gehen, verweisen wir für weitere Einzelheiten auf den Sourcecode in der Datei line.cpp.

Linien zeichnen

Damit der Betrachter Lichtstrahlen auch als solche erkennt, genügt es nicht, sie einfach als einfarbige Linien zu zeichnen. Vielmehr sollten die Linien ein breites Farbspektrum aufweisen und breiter sein als ein Pixel. Bei der Überlappung von Linien mischen Sie die Farbe additiv, das heißt: Sie addieren die einzelnen Farbwerte. Als Ergebnis erhalten Sie immer einen helleren Ton als die beiden Ausgangsfarben. So führt eine additive Farbmischung vieler verschiedener Farben zu einem reinen Weiß.

Wie bereits erwähnt, folgt der Linien­algorithmus einem sehr einfachen Ansatz. Vor allem in Verbindung mit dem additiven Shading erfüllt er seinen Zweck. Eine zu zeichnende Linie sei durch ihre zwei Endpunkte (x0, y0) und (x1, y1) gegeben. Dann berechnen Sie zunächst die maximale Länge der Linie entlang der x- und der y-Achse:

int Laenge = max(abs(x1 - x0), abs(y1 - y0));
		

Wenn Sie nun für jeden Schritt entlang des längeren Achsen­abschnitts die Koordinaten von (x0, y0) nach (x1, y1) interpolieren wollen, benötigen Sie noch die Inkremente:

float dx = (x1 - x0) / Laenge;
float dy = (y1 - y0) / Laenge;
		

Damit könnten Sie eine einfache Linie bereits mit folgender Schleife zeichnen:

x = x0;
y = y0;
while(Laenge-- > 0)
{
	DrawPixel(x, y);
	x += dx;
	y += dy;
}
		

Im Vergleich zu schnelleren Linien­algorithmen setzen Sie bei diesem Verfahren eventuell zu viele Pixel. Da die Lichtstrahlen aber eine gewisse Farbe und Helligkeit mitbringen und sich diese bei überlagerten Lichtstrahlen additiv mischen, ist dies der Darstellungs­qualität nur zuträglich.

Um dickere Linien zu erhalten, setzen Sie nicht einfache Pixel, sondern zeichnen additiv einen kleinen (4 x 4 Pixel großen) Bereich. Diese kleinen Objekte nennt man auch Shadebobs.

Shadebobs zeichnen

Dieser Demoeffekt arbeitet – abgesehen vom Zeichnen des Logos – fast ausschließlich mit additivem Shading. Deshalb sollten Sie an dieser Stelle einen Blick auf die Vorteile von MMX-Befehlen beim Einsatz einer Farbtiefe von 32 Bit werfen. Da die verwendete Demobibliothek demosys.cpp mit 16 Bit Farbtiefe arbeitet (was aufgrund der Abwärts­kompatibilität nicht geändert werden soll), müssen Sie das Resultat danach wieder von 32 auf 16 Bit Farbtiefe reduzieren.

Das Prinzip von MMX (Multimedia Extensions) ist es, auf mehrere verschiedene Werte dieselbe Instruktion anzuwenden. Diese Werte liegen alle zusammen in einem 64 Bit breiten MMX-Register. Zum Beispiel können Sie in solch einem Register vier 16-Bit-Wörter ablegen und diese dann – jedes für sich – mit einem einzigen Befehl nach links oder rechts shiften. Dieses zugrunde­liegende Prinzip heißt SIMD (Single Instruction Multiple Data).

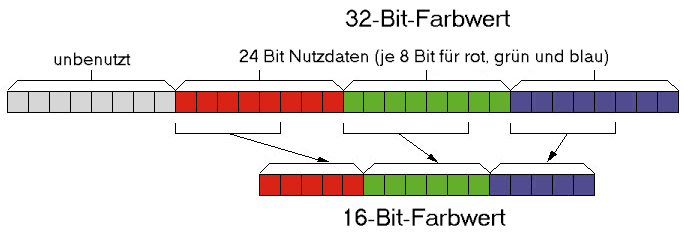
Bei einem 32-Bit-Farbwert, wie Sie ihn verwenden, sind die einzelnen Bits wie im Bild auf S. 217 verteilt. Beim additiven Shading zweier Farbwerte addieren Sie jeweils die Rot-, Grün- und Blauanteile. Falls ein solches Zwischen­ergebnis den maximal mit 8 Bit darstellbaren Wert 255 überschreitet, setzen Sie es auf eben diesen Wert.

Ihr Vorgehen sieht in Pseudocode also folgendermaßen aus:

Farbe1: (r1, g1, b1)
Farbe2: (r2, g2, b2)

Resultat:
r = min(255, r1 + r2)
g = min(255, g1 + g2)
b = min(255, b1 + b2)
		

Sehr entgegen­kommend ist an dieser Stelle MMX, da es einen Befehl zur Verfügung stellt, der genau diese Aufgabe erledigt: paddusb (vgl. dazu die Tabelle auf der rechten Seite unten).

Da sich der Befehl über 64 Bit „erstreckt“, bearbeiten Sie damit sogar zwei Pixel gleichzeitig. Ein Teil des Shadebob-Codes könnte also so aussehen (dieser Code zeichnet zwei Pixel additiv):

;edi-Register mit Adresse
;des 32 Bit Grafikbildes laden
mov edi, [screen32]
;Berechnung von:
;eax=Y*SCREEN_X+X
mov eax, [y_koordinate]
mov ecx, SCREEN_X
mul ecx
add eax, [x_koordinate]
;mal 4, da 32-Bit-Werte
shl eax, 2
;und auf edi addieren
add edi, eax
;64 Bit (zwei Farbwerte) in das
;mm0-Register lesen
movq mm0, [edi]
;additiv shaden
paddusb mm0, [zwei_additive_farbwerte]
;zurückschreiben
movq [edi], mm0
		

Wie Sie sehen, stellt MMX gerade für solche Operationen sehr mächtige Befehle zur Verfügung. Additives Shading mit herkömmlichen Befehlen läßt sich in 32 Bit nur sehr umständlich realisieren, oder Sie müssen dafür einen hohen Rechenaufwand in Kauf nehmen. Bei 16Bit-Werten könnten Sie mit einer Look-Up-Tabelle arbeiten.

Da Sie beim additiven Shading mit MMX-Befehlen 32-Bit-Farbwerte verwenden, müssen Sie diese in 16-Bit-Werte konvertieren. Im Bild auf S. 217 sehen Sie, welche Bit­verschiebungen dazu nötig sind. Intel bietet auf seinen Internet-Seiten unter www.intel.com verschiedene MMX-Anwendungs­beispiele für Entwickler, darunter auch eines mit der gesuchten Funktionalität. Dieses Programm maskiert jeweils die obersten 5 bzw. 6 Bit eines Farbkanals im 32-Bit-Farbwert aus und schiebt sie an die entsprechende Stelle des resultierenden 16-Bit-Werts.

Die entsprechende Routine finden Sie angepaßt im Quellcode des Demoeffekts. Mehr über ein paar ausgewählte MMX-Befehle lesen Sie in der Textbox unten.

Weitere Features

Die Lichtquelle wäre relativ langweilig, wenn die Lichtstrahlen immer in dieselbe Richtung zeigen würden. Für Abwechslung sorgt eine einfache Drehung aller Richtungs­vektoren mit Drehwinkeln, die Sie am besten abhängig von der Zeit berechnen. Damit verpassen Sie der Lichtquelle eine viel interessantere Bewegung und eine Farbänderung, da sich die verschieden eingefärbten Lichtstrahlen jetzt auch in anderen Konstel­lationen überlappen.

Während Sie das Bild konvertieren, können Sie noch einen weiteren Effekt zu den Lichtstrahlen hinzufügen: Wenn die Lichtquelle direkt in das Auge des Betrachters scheint, er also eigentlich geblendet wird, erhöhen Sie die Helligkeit des ganzen Bildes. Das erreichen Sie ganz einfach, indem Sie zu jedem gelesenen 32-Bit-Wert einen Grauwert addieren. Die Helligkeit dieses Werts bestimmen Sie je nach Sichtbarkeit der Lichtquelle. Je mehr Lichtstrahlen den Betrachter direkt ins Auge treffen, um so heller der Grauwert.

Die Intensität der Blendung berechnen Sie zum Beispiel, indem Sie die zwei­dimensionalen Koordinaten der Lichtquelle betrachten und überprüfen, wie viele Pixel in der Umgebung dieser Position vom Logo verdeckt werden oder sichtbar sind. Je mehr ungesetzte Pixel sich dort befinden, desto stärker hellen Sie das Bild auf.

Die zwei­dimensionalen Koordinaten erhalten Sie durch die oben vorgestellte Projektions­formel. Der Code in den folgenden Zeilen verwendet eine 4 x 4 Pixel große Umgebung der Lichtquelle als Maß der Helligkeit:

//Adresse des Pixels, hinter dem die Lichtquelle liegt
int adr = light2dx + light2dy * SCREEN_X;
adr -= SCREEN_X * 4 - 4;

int helligkeit = 0;
for(int j = 0; j < 8; j++)
{
	for(int i = 0; i < 8; i++)
	{
		if (logo[adr] == 0)
			helligkeit++;
		adr++;
	}
	adr += SCREEN_X - i;
}
		

Den Farbwert, mit dem Sie das Bild aufhellen, erhalten Sie wie folgt:

int64 flashlight;

int temp=helligkeit * 4;
//ersten Farbwert verdoppeln,
flashlight=(temp << 16) |
	(temp << 8) | temp;

// damit zwei 32 Bit Werte in
//einem 64-Bit-Wert stehen
flashlight |= flashlight << 32;
		

Blenden- und Fokussierungseffekte

Wenn Sie sich mit Fotografie beschäftigen, vielleicht sogar eine Spiegelreflex­kamera besitzen, wissen Sie um die Probleme der Linsen­abbildungen und kennen den folgenden Demoeffekt vielleicht schon aus der Realität. Um ein Foto mit einer sehr hohen Tiefenschärfe zu erzielen (das heißt, es sollen sowohl nahe als auch weit entfernte Gegenstände scharf zu erkennen sein), muß die Blende eines Fotoapparats so weit wie möglich geschlossen sein. Dieser Vorgang heißt Abblenden.

Noch einmal für Nicht-Fotografen: Die Öffnung, durch die das Licht auf das Filmmaterial fällt, soll klein sein. Vielleicht haben Sie ja schon einmal eine Lochkamera gebastelt und festgestellt, daß das Bild schärfer wird, je kleiner Sie das Loch stanzen. Aus dem gleichen Grund kneifen Sie auch Ihre Augen zu, wenn Sie etwas noch schärfer sehen möchten. Den dadurch erkauften geringeren Lichteinfall gleichen Sie beim Fotografieren mit einer längeren Belichtungs­zeit und beim Blinzeln mit erweiterten Pupillen aus.

Wenn Sie es genau umgekehrt machen, also die Blende Ihrer Kamera weit öffnen, sehen Sie auf dem Foto nur das genau fokussierte Objekt scharf. Mit dieser Technik heben Sie zum Beispiel ein porträtiertes Gesicht vom unscharfen Hintergrund ab.

Das Programm, mit dem Sie die Schärfentiefe variieren, ist lediglich ein kleiner Mehrzeiler. Die Bilderfolge links oben zeigt Ihnen verschiedene Fokussierungs­ebenen, auf die „scharf gestellt“ wurde: Der Schärfebereich bewegt sich dabei von den vorderen Säulen über den Schriftsatz bis zu den hinteren Säulen. Die gleiche Szene sehen Sie im Bild oben, diesmal mit perfekter Tiefenschärfe. Die fehlenden Bilder für einen fließenden Übergang von einer Schärfeebene zur nächsten berechnen Sie mit einer einfachen linearen Interpolation.

Auch das hört sich schwieriger an, als es eigentlich ist. Wenn Sie die gezeigten Bilder der Reihenfolge nach durch­numerieren, können Sie die fehlenden Bilder dazwischen durch Kommazahlen angeben. Um zum Beispiel das Bild mit dem Indexwert 2,3 zu erhalten, berechnen Sie für jedes Pixel aus dem zweiten und dritten Bild die dazugehörige Mischfarbe.

Diese Mischfarbe erhalten Sie, indem Sie die Rot-, Grün- und Blau­komponenten der jeweiligen Pixel mit der entsprechenden Gewichtung multiplizieren und addieren:

Nummer des Vorgänger-Bildes:
2.3 abgerundet, also 2
Nummer des Nachfolger-Bildes:
2.3 aufgerundet, also 3

Faktor für das Vorgänger-Bild:
1.0 - (2.3 - 2) = 0.7 = 70 %

Faktor für das Nachfolger-Bild:
2.3 - 2 = 0.3 = 30 %
		

Es ist auch für diesen Effekt wieder sinnvoll, wenn Sie die Bilder mit den verschiedenen Fokussierungs­stufen in TrueColor (also 32 Bit pro Pixel) im Speicher behalten. Das Beispiel­programm konvertiert die Bilder dann anschließend beim Programmstart in dieses Format.

Nun durchlaufen Sie in einer Schleife alle Pixel der Bilder und berechnen die Mischfarbe. In unserem Beispiel besitzt mix den Wert 0.3, source1 zeigt auf das zweite Bild und source2 auf das dritte Bild:

//Faktoren in den Bereich von 0 bis 255 skalieren
//zwecks Integerarithmetik
int factor1 = (int)((1.0f - mix) * 255.0f);

int factor2 = (int)(mix * 255.0f);

for(int i = 0;i < AnzahlPixel; i++)
{
	unsigned long c1, 2;
	int r, g, b;

	c1 = source1[i];
	c2 = source2[i];

	//Rot-, Grün- und Blauwerte mischen
	//Der Shift-Befehl „>> 8“ am
	//Zeilenende macht die
	//Skalierung rückgängig
	r=((c1 >> 16) * factor1 +
		(c2 >> 16) * factor2) >> 8;

	g=(((c1 >> 8) & 255) * factor1 +
		((c2 >> 8) & 255) * factor2) >> 8;

	b=((c1 & 255) * factor1 +
		(c2 & 255) * factor2) >> 8;

	//Und 16 Bit Wert auf den Bildschirm bringen
	screen[i] = Rtab[r] | Gtab[g] | Btab[b];
}
		

Eine Frage ist noch offen: Woher nehmen Sie die vorberechneten Bilder? Die in unserem Beispiel verwendeten Grafikdateien haben wir mit dem frei erhältlichen POV-Raytracer Persistance of Vision berechnet. Er verfügt über einen großen Funktions­umfang und kann Bilder mit Tiefenschärfe berechnen. Die Definition einer 3D-Szene legen Sie dabei je nach verwendetem Tool mit Hilfe einer Skriptsprache fest, oder Sie generieren sie mit einem Editor. Die Skriptdatei zu unserer Testszene finden Sie ebenfalls bei den Quelltexten auf der Heft-CD.

Das Raytracing-Programm einschließlich Beispielszenen, Anleitungen, Editoren und allem, was dazugehört, bekommen Sie völlig umsonst im Internet unter www.povray.org

Einblicke in die Arbeitsweise eines solchen Raytracers erhalten Sie in einer der kommenden Ausgaben, wenn wir in der Rubrik PC Underground einen mehrteiligen Workshop zum Thema Strahlen­rückverfolgung starten. Dabei werden Sie selbst ein komplettes Raytracing-Programm schreiben.

Nächsten Monat widmen wir uns den populären MP3-Musikdateien und zeigen Ihnen, wie Sie ein Plugin für den beliebten MP3-Player WinAmp programmieren.