Digitaler Schraubstock

Carsten Dachsbacher

Um Multimedia-Daten in ein handliches Format zu bringen, müssen sie effektiv komprimiert sein. Auch Text- und Grafikdateien können Sie um ein Vielfaches schrumpfen. In dieser und den folgenden Ausgaben lernen Sie Pack-Algorithmen und die theoretischen Grundlagen dazu kennen (vgl. die Textbox „Am Anfang war das Bit“ auf S. 254).

RLE-Kompression

Die Lauflängen­codierung (Run Length Encoding, RLE) ist ein intuitives Verfahren. Tritt ein Zeichen Z mehrmals in Folge in der Eingabe auf, schreiben Sie in der Ausgabe nur ein einzelnes Zeichen. Damit Sie wissen, wie oft dieses Zeichen an dieser Stelle vorkommt, stellen Sie die Anzahl n voran. Der Wert n heißt auch die Run Length des Zeichens Z an dieser Stelle. Als Beispiel behandeln Sie in einem Buchtext die Kapitel­überschrift 2. Datenkompression mit der RLE-Methode.

Es gibt drei Möglichkeiten:
• Wenn Sie die doppelte Buchstaben­folge ss durch 2s ersetzen, können Sie das zur Kompression eingesetzte Zahlzeichen 2 nicht von der Kapitel­numerierung unterscheiden und den Originaltext nicht eindeutig wieder­herstellen. Verwenden Sie daher ein nicht benötigtes Zeichen wie @ als Escape-Code. Sein Auftreten im komprimierten Text signalisiert, dass eine Längenangabe folgt: 2. Datenkompre@2sion In unserem Beispiel wird der Originaltext ein Byte länger. Es lassen sich aber Beispiele konstruieren, bei denen eine Schrumpfung auftritt.
• Anstatt des Escape-Codes können Sie vor jedem Zeichen dessen Run Length vermerken:

121.1
1D1a1t1e1n1k1o1m1p1r1e2s1i1o1n
		

Dieser Ansatz lohnt sich jedoch nur bei längeren Zeichenketten, die größere Blöcke gleicher Zeichen enthalten.
• Die eleganteste Methode: Legen Sie eine minimale Anzahl von Wiederholungen fest, ab der Sie ein Zeichen ersetzen. Im folgenden Beispiel beträgt der Minimalwert drei Zeichen: Nur wenn das gleiche Zeichen dreimal oder öfter in Folge auftritt, vermerken Sie nach dem dritten Zeichen, wie oft es noch wiederholt werden soll. So arbeitet auch der Algorithmus im Listing rle.cpp:

abba -> abba
abbbbbba -> abbb3a
abbba -> abbb0a
		

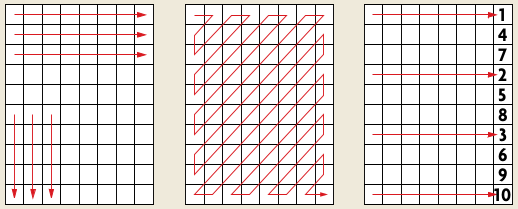
Das PCX-Dateiformat verdichtet Schwarzweiß-Grafiken und Bilder mit einer Palette mit dem RLE-Verfahren. Benachbarte Pixel gleicher Farbe wie im Bild links unten werden so platzsparend zusammengefaßt.

Der Grad der Kompression hängt vor allem bei Strich­zeichnungen wie in der Abbildung unten stark von der Reihenfolge der Abtastung ab. Neben einem horizontalen Durchlauf der Pixel (zeilenweise Abtastung) können Sie die Pixel auch vertikal (spaltenweise) oder im Zickzack-Muster abarbeiten (siehe Abbildung auf S. 254. Sie können die Zeilen bzw. Spalten in beliebig vertauschter Reihenfolge behandeln.

LZW-Kompression

Das komplexe LZW-Verfahren (benannt nach den Initialien seiner Erfinder) führt zu deutlich besseren Ergebnissen als die Lauflängen­kodierung. Dem Verfahren liegt der von Lempel und Ziv erfundene LZ78-Algorithmus zugrunde, an dem Welch einige Modifikationen und Optimierungen vorgenommen hat.

Unter anderem der Dateipacker gzip aus der Unix-Welt sowie verschiedene Bildformate wie Graphics Interchange Format (GIF) und Tagged Image File Format (TIFF) verwenden das LZW-Verfahren. Inzwischen hat die Firma Unisys das Patentrecht an diesem Algorithmus: Eine kommerzielle Nutzung ist nur mit ihrer Erlaubnis gestattet.

Die Kompression beruht auf einem Dictionary (Wörterbuch). Dieses baut der Algorithmus während des Komprimier­vorgangs selbständig auf. Um später wieder an die Originaldaten heranzukommen, brauchen Sie dieses Dictionary nicht mit zu speichern.

Das Wörterbuch besteht aus einer Liste von Strings unterschied­licher Länge. Es umfaßt zu Beginn des Kompressions­vorgangs in den ersten 256 Einträgen (0 bis 255) alle ASCII-Zeichen, also nur ein Zeichen lange Strings.

Der Encoder liest ein Zeichen nach dem anderen ein und reiht sie in einem String aneinander. Dann durchsucht er das Wörterbuch nach dieser Zeichenkette. Findet er sie nicht, bricht er diesen Prozess ab. Wenn der bisherige String I noch im Wörterbuch verzeichnet ist, lässt das nächste Zeichen z die Zeichenkette auf Iz wachsen.

Besitzt diese keinen Eintrag im Dictionary, führt der Encoder folgende Schritte durch:
• Er schreibt den Index des Strings I im Wörterbuch in die Ausgabe.
• Er fügt den String Iz dem Wörterbuch hinzu.
• Er überschreibt den bisherigen String I mit dem Zeichen z.

Anhand des Eingabetextes sir_sid_eastman_easily_teases_sea_sick_seals können Sie sich die Vorgehensweise veranschau­lichen: Zunächst initialisieren Sie das Wörterbuich wie oben beschrieben mit den ASCII-Zeichen und belegen den String I mit einer leeren Zeichenkette. Dann liest der Encoder das Zeichen s, welches sich als Einzelzeichen im Wörterbuch befindet. Das nächste Zeichen lautet i, der String si besitzt allerdings keinen Eintrag im Dictionary. Daher schreibt der Encoder den Index von s (115) an die Ausgabe, fügt den String si an der Position 256 dem Wörterbuch hinzu und belegt den String I mit dem Zeichen i.

So setzt sich der Prozeß bis zum Ende fort, die Ausgabe enthält dann folgende Nummern (in Klammern stehen die zugehörigen Strings, die nicht in der Ausgabe enthalten sind):

115(s), 105(i), 114(r), 32(_),
256(si), 100(d), 32(_), 101(e),
97(a), 115(a), 116(t), 109(m),
97(a), 110(n), 262(_e),
256(si), 108(l), 121(y),
32(_), 116(t), 263(ea),
115(s), 101(e), 115(s),
256(_s), 263(ea), 259(_s),
105(i), 99(c), 107(k),
280(_se), 97(a), 108(l),
115(s), eof(end of file).
		

Das Wörterbuch sieht dann ausschnitts­weise so aus:

0-255 ASCII Codes
256 si
257 ir
258 r_
259 _s
260 sid
261 d_
...

285 _sea
286 al
287 ls
		

Nun stellt der Decoder die Originaldaten wieder her. Er startet wieder mit dem Wörterbuch, das nur die 256 ASCII-Zeichen enthält. Er liest nacheinander die Werte aus den komprimierten Daten und schreibt die zugehörigen Strings an die Ausgabe. Das Wörterbuch baut er dabei genauso auf wie der Encoder. Man sagt daher auch, dass Encoder und Decoder synchronisiert sind bzw. in „lockstep“ arbeiten.

Im Detail: Der Decoder liest den ersten Wert und benutzt ihn, um einen String I aus dem Wörterbuch zu lesen. Die Zeichen dieses Strings werden an die Ausgabe geschrieben. Als nächstes müßte der String Iz ins Wörterbuch eingetragen werden. Das Zeichen z des nächsten Strings ist nun eigentlich noch unbekannt. Aber Sie wissen ja, dass es sich dabei nur um das erste Zeichen des nächsten Strings handeln kann.

Ein Index, den Sie in den Output-Stream des Encoders schreiben, beansprucht bei einer Wörterbuch­größe von maximal 4096 Strings 12 Bit. Ist das Wörterbuch voll, können Sie mit einer von drei Varianten fortfahren:
• Sie können einfach den ältesten oder den am längsten nicht mehr benutzten String mit dem aktuellen String überschreiben.
• Oder Sie vergrößern das Wörterbuch nachträglich. Für Encoder und Decoder müssen Sie immer die gleiche Strategie verfolgen.
• Eine andere Methode ist, einfach keine neuen Strings mehr zuzulassen. Wenn Sie Strings nie entfernen, können Sie das Wörterbuch als verkettete Liste speichern und dadurch sehr viel Speicherplatz sparen. Das Wörterbuch würden Sie dann so definieren:

struct dictionary
{
	int parent, character;
} dict[4096];
		

Dabei ist parent der Index des alten Strings und character der Code (0-255) des letzten ASCII-Zeichens.

Die Wahl der Ersetzungs­strategie ist sehr entscheidend für die erzielten Kompressions­raten bei LZW-Algorithmen. Aber auch die Größe des Wörterbuchs spielt eine große Rolle. Die optimale Größe hierfür hängt von den Eingangsdaten ab.

Huffman-Codierung

Die Huffman-Codierung arbeitet nicht mit einem Wörterbuch, sondern mit der Wahrschein­lichkeit der Eingabe­zeichen. Sie ordnet allen Eingabezeichen Bitcodes unterschied­licher Länge zu. Diese Huffman-Codes sind um so kürzer, je häufiger das Zeichen auftritt.

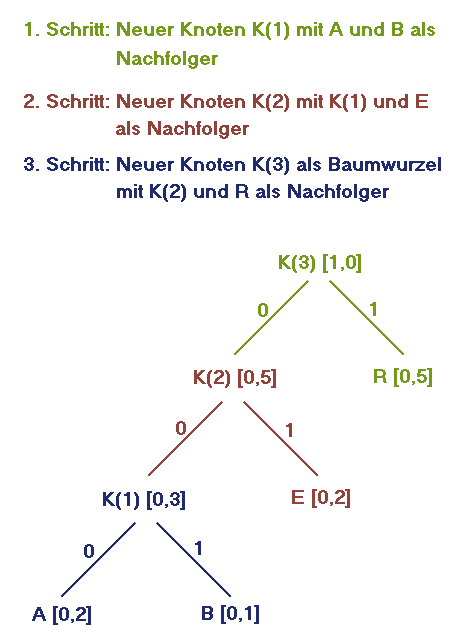
Zur Darstellung dient der Huffman-Baum: ein Binärbaum, dessen Blätter den Eingabezeichen entsprechen und mit ihren Wahrscheinlich­keiten beschriftet sind. Die weiteren Knoten des Baums sind mit der Summe der Wahrscheinlich­keiten der Knoten der nächsthöheren Ebene markiert. Die Kanten bezeichnen wir mit den binären Werten 0 oder 1.

Angenommen, Sie haben die Menge der Eingabezeichen x(1),...,x(n) mit den Wahrschein­lichkeiten p(1),...,p(n). So bauen Sie den Baum auf:
• Suchen Sie die zwei Zeichen x(i) und x(j) mit den kleinsten Wahrschein­lichkeiten.
• Bilden Sie einen neuen Knoten K(ij), und ordnen Sie ihm die Wahrschein­lichkeit p(K(ij)) = p(i) + p(j) zu. Verbinden Sie K(ij) mit x(i) und x(j), und beschriften Sie die Kanten mit den Werten 0 und 1.
• Entfernen Sie x(i) und x(j) aus der Menge der Zeichen, und fügen Sie stattdessen K(ij) hinzu.
• Ist noch mehr als ein Element in der Menge der Eingabezeichen enthalten, gehen Sie wieder zu Schritt 1.
• Machen Sie den letzten hinzugefügten Knoten zur Wurzel des Baums.

Die Skizze oben verdeutlicht die Vorgehensweise für einen Text mit den Zeichen A (p(A) = 0,2), B (p(B) = 0,1), E (p(E) = 0,2) und R (p(R) = 0,5). Bauen Sie den Baum von den Blättern bis zur Wurzel auf. Die Bitfolgen für die Zeichen erhalten Sie, indem Sie die Baumäste von der Wurzel bis zu einem Blatt hinab verfolgen und sich dabei die Bits merken:

A 000
B 001
E 01
R 1
		

Dadurch, dass kein Code der Anfang eines anderen Codes ist, können Sie codierte Wörter wie

EBER 01001011
RABE 100000101
		

eindeutig decodieren. Dazu muss der Encoder die Bitcodes oder den Baum zuvor gespeichert haben.

Wenn Sie komprimierte Daten decodieren wollen, gehen Sie wie folgt vor: Sie starten bei der Wurzel des Baums als aktueller Knoten. Dann lesen Sie ein Bit. Hat es den Wert 0, gehen Sie zum Knoten an der linken Kante Ihres aktuellen Knotens. Beim Wert 1 gehen Sie an der rechten Kante entlang.

Diesen Vorgang wiederholen Sie so lange, bis Sie an einem Blatt des Baums angelangt sind. Dann geben Sie das entsprechende Zeichen aus und springen zurück zur Wurzel. In C-Code könnte das so aussehen:

//towrite enthält Anzahl der Outputbytes
while(towrite > 0)
{
	//Bit lesen
	int bit = getcode(1);
	if(bit == 0) actnode = tree[actnode].left;
	else actnode = tree[actnode].right;

	if (actnode < 256)
	{
		//Blatt gefunden!
		putc(actnode, g);
		towrite–;
		actnode = nodes-1;
	}
}
		

Statt alle Zeichen­wahrschein­lichkeiten zu Beginn abzuzählen, können Sie sie ständig während der Codierung anpassen (Adaptives Huffman Coding). Vorteil: Der Encoder passt sich immer den aktuell auftretenden Wahrschein­lichkeiten an und erzielt dadurch bessere Kompressions­raten. Voraussetzung: Die Anpassung muss schnell erfolgen und die Wahrschein­lichkeiten dürfen sich nicht zu schnell ändern.

In der Praxis finden Sie bei einem Packprogramm meist nicht nur einen Algorithmus, sondern fast immer eine Kombination aus einem Dictionary-Packer und einem statistischen Encoder wie beim Huffman-Algorithmus. Zum Beispiel können die Indizes, die beim LZW-Verfahren als Ausgabe entstehen, als Eingabezeichen für einen Huffman-Packer dienen. Dadurch erzielen Sie deutlich bessere Kompressions­raten als bei der Anwendung nur eines Verfahrens.

Um ungewollten Datenverlusten vorzubeugen, entwickeln Sie zu jedem Packer immer sofort auch den zugehörigen Entpacker. Danach sollten Sie beide einem ausgiebigen Test unterziehen: Was nützt die kleinste Datei, wenn darin nicht mehr alle nötigen Informationen zum Entpacken enthalten sind?

Der LZW-Packer aus dieser Ausgabe gibt Ihnen viel Raum für eigene Experimente. In der nächsten Ausgabe stellen wir Ihnen ausgefeilte Algorithmen für Spezial­anwendungen vor.