Nacht und Nebel

Carsten Dachsbacher

Die 3D-Grafikkarten erlauben es, 3D-Szenen mit einem Nebeleffekt zu versehen. Der Programmierer kann diese Funktionalität mit Parametern festlegen: die Dichte des Nebels oder dessen exponenziellen bzw. linearen Verlauf.

Stimmungsvolle 3D-Szenen, beispielsweise nur mit Bodennebel, lassen sich damit nicht darstellen. Wir zeigen Ihnen, wie Sie die volumetrischen Nebeleffekte programmieren. Volumetrisch bedeutet, das der Nebel in einem bestimmten Volumen eingeschlossen ist, etwa in einem Quader, einem Zylinder oder einer Kugel.

OpenGL Fogging

Nebel, wie Sie ihn im obigen Bild sehen, kann Ihre Grafikkarte selbstständig darstellen. Dafür gibt es Unterstützung seitens der Hardware und der Grafik-APIs. Die Grafik-Hardware berechnet für jeden Vertex oder jeden Pixel (je nach Modus) die Entfernung der dort sichtbaren Oberfläche zum Betrachter. Abhängig von dieser Entfernung ist der Nebeleffekt stärker oder schwächer.

In OpenGL aktivieren Sie den Nebel (Fogging) mit glEnable(GL_FOG). Anschließend müssen Sie die Parameter für das Fogging angeben. Legen Sie den Tiefen-Bereich fest, in dem sich der Nebel befindet. Dazu geben Sie einen Start- und einen Endwert an und legen die Dichte des Nebels und die Farbe fest:

glFogf(GL_FOG_START, 0.0f);
glFogf(GL_FOG_END, 100.0f);
glFogf(GL_FOG_DENSITY, 1.0f);
GLfloat fogColor[] = { 1.0f, 1.0f, 1.0f, 1.0f };
glFogfv(GL_FOG_COLOR, fogColor);
		

Für die Berechnung der Nebel­intensität f, abhängig von der Entfernung z, wählen Sie mit dem Eintrag glFogi(GL_FOG_MODE, mode) eine der folgenden drei Optionen:

GL_LINEAR f = (end - z) / (end - start)
GL_EXP f = e^(-density * z)
GL_EXP2 f = e^((-denstity * z)^2)
		

Diese Optionen bestimmen, wie die Stärke des Effekts von der Entfernung z und dem Start- bzw. End-Wert des Nebels abhängt.

Als nächstes berechnen Sie die Farbe jedes Pixels im Nebel, abhängig vom Wert f. Die ursprüngliche Farbe wird in die Nebelfarbe übergeblendet, wobei sich der Bereich f von 0 bis 1 beschränkt:

//für jede Farbkomponente:
color_new = f * color + (1 - f) * fogColor
		

Volumetric Fog

Wenn Sie die Nebelschwaden berechnen, kommen Sie mit volumetrische Nebeleffekten zu eindrucks­vollen Bildern.

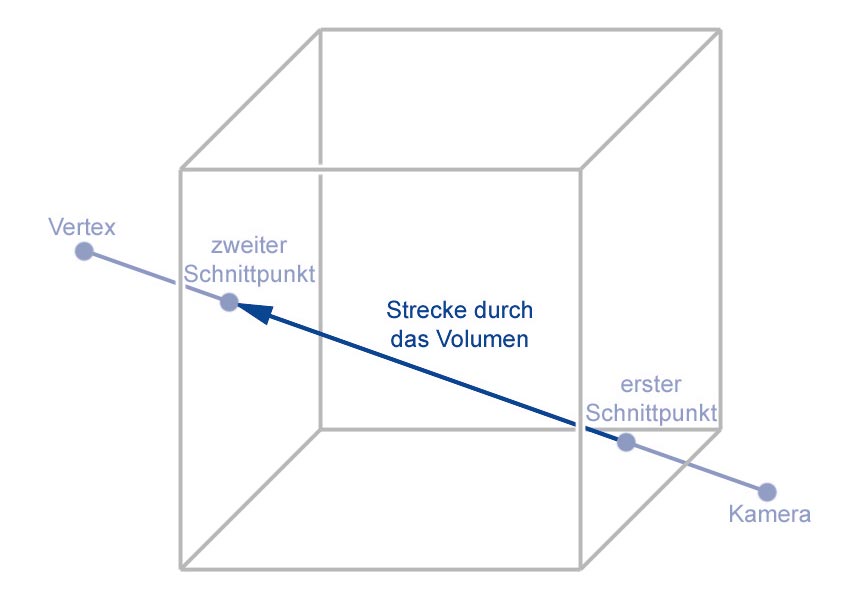
Lesen Sie, wie Sie diese Effekte ohne die OpenGL-Fog-Funktionalität gestalten. Als mögliche Volumina für den Nebel kommen einfache geometrische Primitive wie Quader, Zylinder oder Kugeln oder daraus zusammen­gesetzte Primitive in Betracht. Das befähigt Sie, den Nebel schnell zu berechnen. Der Trick besteht darin, für jeden Vertex der sichtbaren 3D-Objekte die Nebel­intensität zu berechnen. Diese Intensität hängt davon ab, wieviel Nebel sich zwischen Kamera und Objekt befindet. Da Sie die Intensität pro Vertex berechnen, bestimmen Sie zunächst die Halbgerade (Strahl), beginnend bei der Kameraposition in Richtung des Vertex.

Anschließend berechnen Sie alle Schnittpunkte des Strahls und der Nebelvolumina. Es gibt nicht für jeden Strahl einen Schnittpunkt. An Hand der Schnittpunkte können Sie die Länge der im Nebel zurückgelegten Strecken und somit die Nebel­intensität bestimmen.

Wir zeigen Ihnen Schritt für Schritt, wie Sie das Grundprinzip umsetzen, um quader- und kugelförmige Nebelvolumina darzustellen. Voraussetzung ist, dass Sie ein geladenes 3D-Objekt im Speicher haben, bestehend aus einer Vertex und einer Flächen-Index-Liste:

typedef struct
{
	float x, y, z;
} VERTEX3D;

typedef struct
{
	int a, b, c;
	VERTEX3D normal;
} FACE;

VERTEX3D *pVertexList;
FLOAT *pFogList;
VERTEX3D *pNormalList;
FACE *pFaceList;
int nVertices, nFaces;
		

Bestimmen Sie für jeden Vertex – für jeden Frame – die Nebel­intensität. Dazu benötigen Sie eine Halbgerade, die sich aus Koordinaten der Vertex- und der Kameraposition bestimmen lässt. Beide Koordinaten müssen Sie in dasselbe Koordinaten­system transformieren. Dazu bieten sich zwei Wege an:
• Sie führen alle Berechnungen im Objektspace durch und transformieren die Kamera in den Objectspace,
• oder Sie transformieren alle Vertices in den Worldspace, in dem sich die Kamera befindet. Die erste Variante ist weniger zeitaufwändig, da nur die Kameraposition transformiert werden muss. Beginnen Sie mit der Kamera­transformation:

typedef struct
{
	// Ursprung, Richtung
	VERTEX3D from, d;
} RAY3D;

MATRIX44 modelView, invModelView;

// Modelview Matrix holen...
glGetFloatv(GL_MODELVIEW_MATRIX, modelView);

// ... invertieren
InverseMatrixAnglePreserving(modelView, invModelView);
// Kameraposition aus den Kameraeinstellungen bekannt!
VERTEX3D camPos = { 0.0f, 0.0f, 70.0f };

// Start der Halbgerade
// = Kamera im Objectspace !
ray.from = invModelView * camPos;
		

Jetzt bestimmen Sie die Richtung der Halbgeraden für jeden Vertex i:

// Richtung (normalisiert)
ray.d = pVertexList[i] - ray.from;
~ray.d;
		

Anschließend berechnen Sie, ob Schnittpunkte mit Nebelvolumina existieren und wenn ja, die Nebel­intensität. Die Details der verwendeten Subroutinen betrachten Sie folgendermaßen:

// Eckpunkte des Nebelquaders
VERTEX3D minBox = { -100.0f, 0.0f, -100.0f };
VERTEX3D maxBox = { 100.0f, 10.0f, 100.0f };

// Abschnitte an der Halbgerade,
// falls es Schnittpunkte gibt
float tmin, tmax;
if (boxIntersection(ray, &tmin, &tmax,
	minBox, maxBox, pVertexList[i]))
{
	// Schnittpunkte existieren
	fog = distanceInFog(ray, tmin, tmax,
		pVertexList[i]);
}
		

Der Rückgabewert von distanceInFog(...) ist die Strecke, die der Strahl durch das Nebelvolumen zurücklegt. Mit diesem Wert können Sie analog zur OpenGL-Nebel­berechnung einen linearen oder exponenziellen Verlauf modellieren, wie die folgenden Beispiele zeigen:

// linearer Nebel
// einfaches Skalieren
fog *= 0.05f;

// exponenzieller Verlauf
fog *= 0.03f;
fog = exp(fog) - 1;

// exponenziell/quadr.Verlauf
fog *= 0.04f;
fog = exp(fog * fog) - 1;
		

Sie können Lookup-Tabellen verwenden, um Nebelschwaden darzustellen. Das folgende Beispiel verwendet eine Tabelle mit 256 Einträgen für Nebel­intensität, zwischen denen interpoliert wird:

fog *= 255.0f;
if(fog > 254)
	fog = 254;

int fogi = (int)fog;
float fogf = fog - fogi;
fog = table[fogi] * (1.0f - fogf)+
	table[fogi + 1] * fogf;
		

Mit der berechneten Neben­intensität skalieren Sie die gewünschte Farbe des Nebels und speichern diese zusammen mit dem ursprünglichen Wert zunächst für jeden Vertex für das spätere Rendering:

GLfloat fogColor[] = { 0.7f, 0.7f, 0.5f };
float *pFog = pFogList;
*(pFog++) = fog * fogColor[0];
*(pFog++) = fog * fogColor[1];
*(pFog++) = fog * fogColor[2];
*(pFog++) = fog;
		

Schnittpunkt-Berechnungen

In der Routine boxIntersection(...) verbirgt sich die Schnittpunkt-Berechnung zwischen einem Strahl und einem Quader mit achsen­parallelen Kanten (aus Performance-Gründen). Solche Quader werden auch als AABB (Axis Aligned Bounding Boxes) bezeichnet. Dafür gibt es hochoptimierte Schnittpunkt­berechnungen, von denen wir Ihnen eine hier vorstellen: die Slab-Methode. Slab bezeichnet ein paralleles Ebenenpaar. Drei Slabs bilden einen Quader. Im zwei­dimensionalen Fall bilden zwei Slab-Paare ein Rechteck.

Für ein Slab-Paar können Sie die beiden Schnittpunkte berechnen, hier für das X-Slab-Paar:

// Strahl darf nicht parallel zu
// den Ebenen verlaufen
if(fabs(ray.d.x) > epsilon)
{
	tmin_x = (minB.x - ray.from.x) / ray.d.x;
	tmax_x = (maxB.x - ray.from.x) / ray.d.x;
} else
	return 0; // kein Schnittpunkt
		

Bei geschickter Betrachtung der Schnittpunkte oder der berechneten tmin/ tmax-Parameter stellen Sie fest, ob der Strahl die AABB schneidet. Berechnen Sie für jedes der drei Slab-Paare tmin und tmax:

tmin = max(tmin_x, tmin_y, tmin_z)
tmax = min(tmax_x, tmax_y, tmax_z)
		

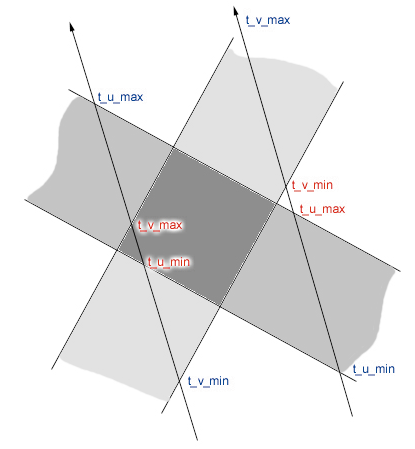
Wenn tmin kleiner oder gleich tmax ist, schneidet der Strahl den Quader, sonst verfehlt er ihn. Betrachten Sie dazu die zwei einge­zeichneten Strahlen im vorigen Bild. Die ausschlag­gebenden tmin und tmax-Werte sind rot gekennzeichnet. Bevor Sie in der boxIntersection(...)-Routine die Slab-Methode anwenden, wird noch ein Trivial-Reject-Test (Rückweisungs-Test) durchgeführt. Dabei überprüfen Sie mit einfachen, rechenzeit­unkritischen Befehlen, ob der Strahl den Quader überhaupt schneiden könnte. Das können Sie beispielsweise ausschließen, wenn sowohl der Ursprung als auch das Ziel des Strahls über, unter oder links bzw. rechts vom Quader liegen.

Als zweites Nebelvolumen verwenden Sie die Kugel, für die sich die Schnittpunkte einfach berechnen lassen. Eine Kugel ist definiert durch ihren Mittelpunkt m und ihren Radius r. Alle Punkte x auf der Oberfläche der Kugel, also auch potenzielle Schnittpunkte mit einer Geraden, haben den gleichen Abstand vom Mittelpunkt, nämlich den Radius:

|x - m| = r
(x - m) * (x - m) = r * r
		

Wenn Sie die (Halb-)Geraden­gleichung in die Abstands­berechnung für x einsetzen, erhalten Sie eine quadratische Gleichung, deren Lösung oder Lösungen die Parameter der Geraden­gleichung sind. In C-Code sieht das Resultat wie folgt aus:

VERTEX3D delta = ray.from - center;
a = ray.d * ray.d;
b = ray.d * delta * 2.0f;
c = center * center +
	ray.from * ray.from -
	2.0f * (center * ray.from) -
	radius * radius;

d = b * b - 4.0f * a * c;
if (d <= 0.0)
	return 0;

d = (float)sqrt(d);
a = 1.0f / (2.0f * a);
t1 = (-b + d) * a;
t2 = (-b - d) * a;

// Schnittpunktparameter
tmin = min(t1, t2);
tmax = max(t1, t2);
		

Mit den tmin/tmax-Parametern, also der Information, wo der Strahl in ein Nebelvolumen eintritt oder es verlässt, können Sie die Strecke berechnen, die er im Nebel zurücklegt. Dabei müssen Sie eine Fallunter­scheidung machen – je nachdem, ob sich der Betrachter und/oder der betrachtete Vertex selbst im Volumen befindet. Diese Bestimmung übernimmt die distanceInFog(...)-Methode, die als Parameter tmin/tmax, die Halbgerade ray und den betrachteten Vertex v bekommt.

Zunächst berechnen Sie, wie weit Sie ausgehend von der Kameraposition in Richtung des Strahls gehen müssen, bis Sie den Vertex v erreichen:

if(ray.d.x != 0)
	tv = (v.x - ray.from.x) / ray.d.x;
else
	// ray.d.y oder ray.d.z
		

Anschließend folgt die Fallunter­scheidung:

// Kamera blickt von der Box weg
if(tmax < 0)
	return 0;

// Fog Volume befindet sich
// hinter dem Vertex
if(tmin > tv)
	return 0;

// Vertex im Fog Volume
if (tv > tmin && tv < tmax)
{
	// Kamera auch im Fog Volume ?
	if (tmin < 0)
		/* ja */ return tv;
	else
		/* nein */ return tv - tmin;
} else
{
	// Fog Volume befindet sich
	// zw. Kamera und Vertex
	return tmax - tmin;
}
		

Volumetrischen Nebel rendern

Um volumetrischen Nebeleffekte ohne spezielle Funktionen oder OpenGL-Extensions zu rendern, verwenden Sie eine 2-Pass-Methode: Sie zeichnen die Szene zweimal.

Im ersten Renderpass zeichnen Sie die 3D-Szene mit den gewünschten Parametern für Beleuchtung, Texturen und Materialien:

// Material Parameter
glEnable(GL_COLOR_MATERIAL);
glColorMaterial(...);
glMaterialfv(...);

// einfach flatshaded Zeichnen
glBegin(GL_TRIANGLES);
for(int i = 0;i < nFaces; i++)
{
	glNormal3fv((float*)&pFaceList[i].normal);
	glVertex3fv((float*)&pVertexList[pFaceList[i].a]);
	glVertex3fv((float*)&pVertexList[pFaceList[i].b]);
	glVertex3fv((float*)&pVertexList[pFaceList[i].c]);
}
glEnd();
		

Im zweiten Renderpass benötigen Sie die oben berechneten Nebel­intensitäten. In diesem Pass zeichnen Sie ohne Beleuchtung und Texturen. Allerdings aktivieren Sie das Blending und wählen additives Rendering: Die Nebelfarbe hellt das Bild auf.

glDisable(GL_TEXTURE_2D);
glDisable(GL_LIGHTING);
glEnable(GL_BLEND);
glBlendFunc(GL_ONE, GL_ONE);

// Interpolation Nebelintensität
glShadeMode(GL_SMOOTH);
		

Nach dieser Initialisierung zeichnen Sie die 3D-Szene und übergeben für jeden Vertex seine Nebelfarbe:

glBegin(GL_TRIANGLES);
for(i = 0; i < nFaces; i++)
{
	glColor4fv((GLfloat*)&pFogList[pFaceList[i].a * 4]);
	glVertex3fv((GLfloat*)&pVertexList[pFaceList[i].a]);
	glColor4fv((GLfloat*)&pFogList[pFaceList[i].b * 4]);
	glVertex3fv((GLfloat*)&pVertexList[pFaceList[i].b]);
	glColor4fv((GLfloat*)&pFogList[pFaceList[i].c * 4]);
	glVertex3fv((GLfloat*)&pVertexList[ pFaceList[i].c]);
}
glEnd();
		

Die Neben­intensitäten, die Sie für die Vertices berechnet haben, werden beim Rendering über die Dreiecke interpoliert. Um eine gute Darstellungs­qualität zu erhalten, benötigen Sie Dreiecksnetze, die fein tesseliert sind (= aus vielen kleinen Dreiecken bestehen). Gegebenenfalls müssen Sie mit einem 3D-Modelling­programm vorhandene 3D-Modelle verfeinern (so genanntes Subdividing). Vor allem, wenn die Grenzen von Nebelvolumina sichtbar sind, benötigen Sie sehr feine 3D-Modelle, oder Sie erhalten störende Effekte.

Schneller im Nebel

Es gibt noch eine andere Art, die Neben­intensitäten zu bestimmen, als lediglich die Strecke zwischen den Schnittpunkten des Strahls und den Nebelvolumina als Wert heranzuziehen: Sie können einem quaderförmigen Nebel eine 3D-Textur zuweisen. Da viele 3D-Karte mit 3D-Texturen nicht arbeiten können, müssen Sie diese Aufgabe selbst in Ihrem Programm lösen. Dazu betrachten Sie den Eintrittspunkt eines Strahls in ein Nebelvolumen und den Austrittspunkt. Dann untersuchen Sie jeden 3D-Texel der Textur, den der Strahl im Nebelvolumen berührt, und summieren deren Intensitäten auf.

So könnten Sie Nebelschwaden und komplexe Strukturen im Nebel darstellen. Allerdings ist diese Methode sehr rechnen­zeitintensiv und bedarf einiger Optimierung.

Beschleunigt rendern Sie anders: Mit einer OpenGL Extension EXT_fog_coord, die Sie beim OpenGL-Treiber anfragen können, gelingt es, einen der Renderpasses einzusparen. Diese Extension erlaubt es, für jeden Vertex eine selbst­berechnete Nebel­intensität anzugeben. Ohne diese Erweiterung berechnet OpenGL bei angeschaltetem Fogging diesen Wert selbst. Mit folgenden Befehlen befragen Sie Ihren Grafikkarten-Treiber, ob er diese Extension anbietet:

const GLubyte *glExtString;
char glExtName[] = "EXT_fog_coord";

glExtString = glGetString(GL_EXTENSIONS);
if(strstr(glExtString, glExtName) == NULL)
{
	// nicht unterstützt !!!
	return false;
}
// sonst Adresse holen:
glFogCoordfEXT = (void*)wglGetProcAddress("glFogCoordfEXT");
		

Zu dieser Extension gehören einige weitere Funktionen für das Rendering mit Streaming- und Interleaved-Daten. Diese finden Sie zusammen mit den benötigten Konstanten­definitionen in der glext.h-Datei.

Bei dieser 1-Pass-Rendering Methode aktivieren Sie wieder das OpenGL-Rendering und teilen ihm mit, dass Sie die Nebel­intensitäten selbst berechnen:

glEnable(GL_FOG);
glFogi(GL_FOG_MODE, GL_LINEAR);
glFogfv(GL_FOG_COLOR, fogColor);
glFogf(GL_FOG_START, 0.0f);
glFogf(GL_FOG_END, 100.0f);
glFogi(GL_FOG_COORDINATE_SOURCE_EXT, GL_FOG_COORDINATE_EXT);
		

Damit reduziert sich das Rendering auf folgende Schleife (analog zum obigen ersten Renderpass):

// Material Parameter
glEnable(GL_COLOR_MATERIAL);

glColorMaterial(...);
glMaterialfv(...);

// einfach flatshaded Zeichnen
glBegin(GL_TRIANGLES);

for(int i = 0; i < nFaces; i++)
{
	glNormal3fv((float*)&pFaceList[i].normal);
	glFogCoordfEXT(pFogList[pFaceList[i].a * 4]);
	glVertex3fv((float*)&pVertexList[pFaceList[i].a]);
	glFogCoordfEXT(pFogList[pFaceList[i].b * 4]);
	glVertex3fv((float*)&pVertexList[pFaceList[i].b]);
	glFogCoordfEXT(pFogList[pFaceList[i].c * 4]);
	glVertex3fv((float*)&pVertexList[pFaceList[i].c]);
}

glEnd();
		

Wie Sie in der obigen Programm­schleife sehen, müssten Sie nicht einmal selbst die Farbe des Nebels mit der Intensität skalieren, da OpenGL das automatisch mit der eingestellten Fog-Farbe tut. Somit würde die pFogList nur noch ein Viertel der Einträge benötigen.