GeForce, OpenGL und Spiegeleffekte

Carsten Dachsbacher

Regelmäßige PC-Underground-Leser kennen die Grundlagen zu Environment Mapping und Rendering von Spiegelungen. Mit dieser Ausgabe erweitern Sie diese Techniken um die Echtzeit­darstellung von Lichtbrechung. Sie sehen, wie verschiedene Materialien Licht reflektieren und brechen. Diese Eigenschaften nutzen Sie, um Ihre 3D-Objekte realistisch wirken zu lassen. Um optimale Performance zu erreichen, verwenden Sie die OpenGL Vertex Shaders, Register Combiners und Cubemaps, die GeForce-Grafikkarten unterstützen.

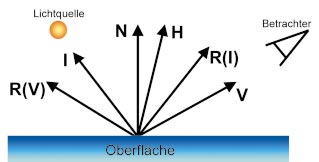
Grundlagen liefert die Geometrie der Reflexion. Das Bild oben zeigt die im Folgenden beschriebenen Vektoren in ihrem Zusammenhang. Wichtig für das Rendering von Spiegelungs­effekten sind die Oberflächen­normale N, der Vektor zur Lichtquelle I, zum Betrachter V und der Halfway- bzw. Halb-Vektor H, den Sie mit der Formel

H = (I + V) / | I + V |
		

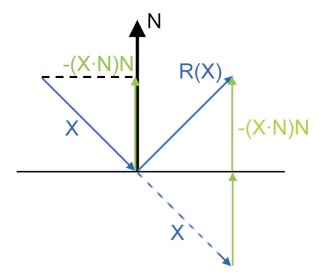
berechnen. Alle Vektoren sind normiert. Einen reflektierten Vektor zu einem beliebigen Vektor X an der Oberfläche mit der Normalen N berechnen Sie mit der Formel

R(X) = X - 2*(X dot N)*N
		

Der Wert dot steht für das Skalarprodukt.

Bei dieser Formel gilt: Einfallswinkel gleich Ausfallswinkel. Unser Beispiel beschreibt eine ideale Reflexion, weil der Strahl auf einen planaren, perfekten Spiegel trifft.

Die ideale Lichtbrechung folgt dem Snell’schen Gesetz. Lichtbrechung tritt an der Grenzfläche zweier Medien (etwa Luft und Wasser) auf. Dabei passiert ein Lichtstrahl nicht einfach die Grenzfläche, sondern ändert auch seine Richtung. Diese setzt die Richtung des einfallenden Lichtstrahls zu der des gebrochenen in Zusammenhang. Die Richtungen hängen auch von der Brechzahl der Medien ab. Die Brechzahl ist ein Maß, wie stark Licht abgelenkt werden kann. Wasser hat eine höhere Brechzahl als Luft.

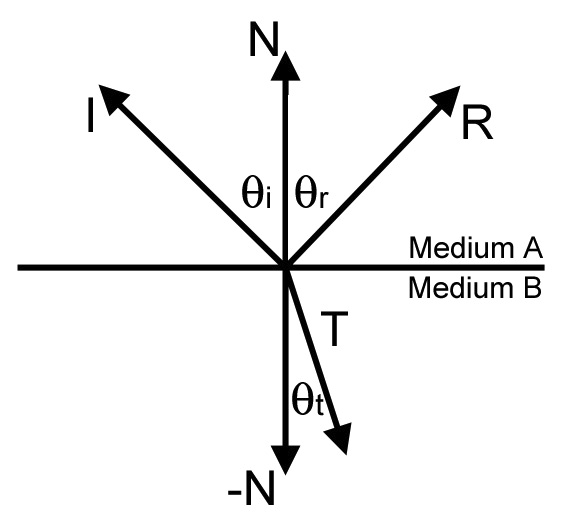
Wenn ein Strahl von einem Medium A ins Medium B eindringt, gilt:

eta = (Brechzahl Medium A) / (Brechzahl Medium B)
sin(theta_i)/sin(theta_t) = eta
		

Die Richtung des gebrochenen Strahls berechnen Sie wie folgt:

IdotN = - I * N
		

Wenn der Term

(1 - eta2 * (1 - IdotN2))
		

kleiner Null ist, liegt eine Totalreflexion vor. Dabei existiert kein gebrochener Strahl, weil das Licht an der Oberfläche reflektiert wird. Dieses Phänomen beobachten Sie auch an den Rändern von Luftblasen unter Wasser. Berechnen Sie einfach den resultierenden Vektor mit

T = eta * I + (eta * IdotN -
	sqrt(1 - eta2 *(1 - IdotN2))) * N
		

Mit den Richtungen der Lichtstrahlen aus Spiegelung und Lichtbrechung können Sie mit der Grafik-Hardware die Farbwerte bestimmen. Zuvor ein Gesetz der Physik, das Sie vereinfacht einsetzen: Das Fresnel’sche-Gesetz beschreibt, wie die Licht­intensitäten aus Reflexion und Refraktion (Brechung) die sichtbare Farbe ergeben. Ein Beispiel: An einem sonnigen Tag betrachten Sie die lackierten Teile eines sauber polierten Autos. Wenn Sie senkrecht auf Flächen blicken, sehen Sie die Farbe des Lacks. Wenn Sie aber in einem sehr flachen Winkel auf eine lackierte Partie sehen, sehen Sie weniger die Farbe als ein Spiegelbild. Bei flachen Winkeln spiegeln solche Flächen eben.

Der Fresnel-Term für unpolari­siertes Licht bestimmt den Bruchteil des gespiegelten Lichts, das der Betrachter wahrnimmt, abhängig von der Wellenlänge lambda des Lichts:

F(lambda) = 0.5 * (g - c)2 / (g + c)2 *
	(1 + [c(g + c) - 1]2 /[c(g - c) + 1]2)
		

mit

c = cos(theta_i) = L dot H,
g2 = eta(lambda)2 + c2 - 1
		

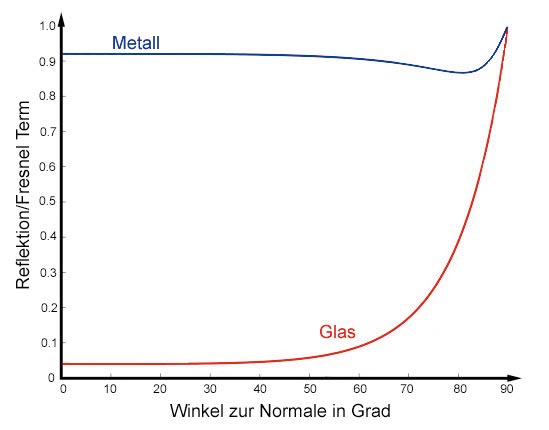
Wir wollen an dieser Stelle nur den Fresnel-Term in einer Näherung betrachten, da die exakte Berechnung nicht für Echtzeit-Rendering einzusetzen und für den optischen Effekt auch nicht notwendig ist. Betrachten Sie dazu die zwei Fresnel-Reflectance-Kurven im Bild.

Um den Fresnel-Effekt in einem Vertex Shader einfach und schnell simulieren zu können, verwenden Sie eine simple Näherung, die für Glas und andere nicht metallische Materialien einsetzbar ist:

F = Fresnelkonstante * ((1 - (I dot N)) ^ p)
		

p ist ein Exponent, im Beispiel­programm ist p = 2.

Diese wenigen einfachen Formeln genügen für beachtliche Resultate, wie die Screenshots unseres Beispiel­programms beweisen..

Einen wesentlichen Beitrag dazu leisten die Cubemap-Features der modernen Grafikkarten. Sie können die Umgebung eines 3D-Objektes in sechs Texturen repräsentieren, die Sie sich wie einen aufgefalteten Würfel vorstellen können.

Die 3D-Hardware kann diese Texturen zusammen adressieren, wobei Sie diese als Environment Textures verwenden können. Die Adressierung der Texel dieser Texturen erfolgt über einen 3D-Vektor, was optimal für Ihre Spiegelungen und Licht­brechungen ist. Aus der Richtung eines Lichtstrahls bekommen Sie mit den Cubemaps den entsprechenden Farbwert! Ausgabe 4/02 behandelt ab S. 206 die notwendigen Initialisierungen, wobei er sich auf das Vertex Programm und die Register Combiner konzentriert.

Als erstes legen Sie die Cubemap Texture mit Skybox-Texturen an, die die Umgebung des 3D-Objekts beinhalten. Als nächstes widmen Sie sich der Entwicklung des Vertex- Programms. Ein Vertex-Programm (Ausgabe 02/02, S. 191) übergeben Sie so an OpenGL:

unsigned int vpFresnelCubemap;
const unsigned char
	vpFresnelCubemapTxt [] = "...";

// Vertex Programm erzeugen...
glGenProgramsNV(1, &vpFresnelCubemap);
// ... auswählen und übergeben
glBindProgramNV(GL_VERTEX_PROGRAM_NV, vpFresnelCubemap);
glLoadProgramNV(GL_VERTEX_PROGRAM_NV, vpFresnelCubemap,
	strlen((char*)vpFresnelCubemapTxt), vpFresnelCubemapTxt);

// und aktivieren
glEnable(GL_VERTEX_PROGRAM_NV);
		

Als Parameter können Sie einem Vertex-Programm die OpenGL-Matrizen oder feste Parameter übergeben. Unser Beispiel­programm benötigt folgende Daten:

// OpenGL Matrizen
glTrackMatrixNV(GL_VERTEX_PROGRAM_NV, 0,
	GL_MODELVIEW_PROJECTION_NV, GL_IDENTITY_NV);

glTrackMatrixNV(GL_VERTEX_PROGRAM_ NV, 4,
	GL_MODELVIEW, GL_INVERSE_TRANSPOSE_NV);

glTrackMatrixNV(GL_VERTEX_PROGRAM_NV, 8,
	GL_MODELVIEW, GL_IDENTITY_NV);

// enthält inverse Kameramatrix
glTrackMatrixNV(GL_VERTEX_PROGRAM_NV, 12,
	GL_TEXTURE, GL_IDENTITY_NV);

// Betrachterpos.
glProgramParameter4fNV(GL_VERTEX_PROGRAM_NV,
	20, 0.0, 0.0, 0.0, 1.0);

// div.Konstanten
glProgramParameter4fNV(GL_VERTEX_PROGRAM_NV,
	23, 0.0, 1.0, 2.0, 3.0);
		

Als weitere Konstanen, die während der Laufzeit geändert werden können, verwenden Sie:

// Brechzahl
glProgramParameter4fNV(GL_VERTEX_PROGRAM_NV,
	22, eta, eta * eta, 0.0f, 0.0f);

// Fresnelkonstante
glProgramParameter4fNV(GL_VERTEX_PROGRAM_NV,
	21, fresnel, fresnel, fresnel,1.0f);
		

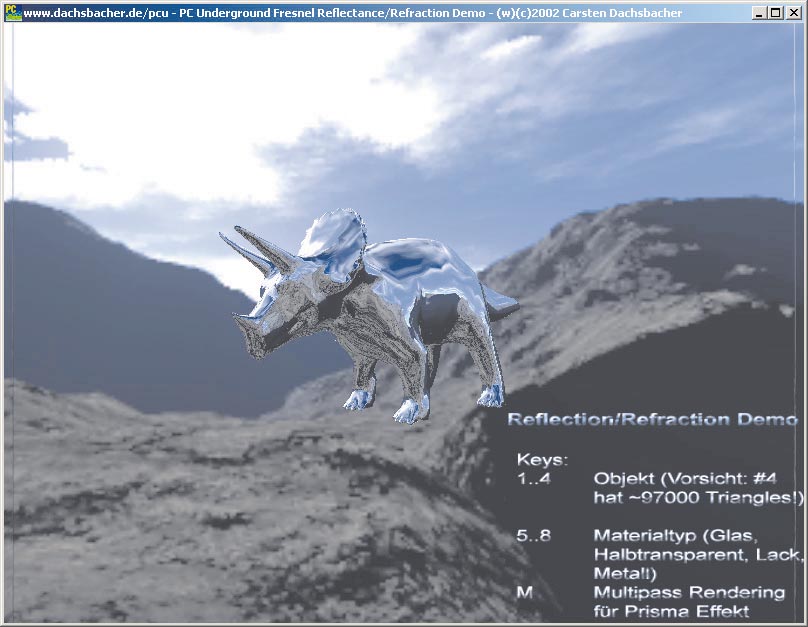
Jetzt führen wir Ihnen Schritt für Schritt das Vertex-Programm vor, das in vpFresnelCubemapTxt steht. Zunächst transformieren Sie die Vertex-Koordinaten aus dem Objectspace in die homogenen Koordinaten des Clipspace. Dazu benötigen Sie die Modelview-Projection Matrix, die sich in den Vertex-Programm-Parametern c[0] bis c[4] befindet:

!!VP1.0
DP4 o[HPOS].x, c[0], v[OPOS];
DP4 o[HPOS].y, c[1], v[OPOS];
DP4 o[HPOS].z, c[2], v[OPOS];
DP4 o[HPOS].w, c[3], v[OPOS];
		

Damit haben Sie die notwendige Arbeit für die Geometrie­transformation geleistet. Jetzt geht es daran, die Texture-Koordinaten für die Cubemaps zu berechnen. Diese Koordinaten entsprechen den Richtungen des Reflexions- und Transmissions­strahls. Für diese Berechnungen bringen Sie zunächst die Normalen und die Vertex-Positionen in den Eye Space (Koordinaten­system, in dem sich der Betrachter bei (0, 0, 0, 1) befindet):

DP3 R5.x, c[4], v[NRML];
DP3 R5.y, c[5], v[NRML];
DP3 R5.z, c[6], v[NRML];
DP4 R0.x, c[8], v[OPOS];
DP4 R0.y, c[9], v[OPOS];
DP4 R0.z, c[10], v[OPOS];
DP4 R0.w, c[11], v[OPOS];
		

Den Vektor von der Vertexposition zum Betrachter erhalten Sie durch Subtraktion (-R0!) mit

#R0 = c[20] - R0
ADD R0, -R0, c[20];
		

Diesen gilt es zu normieren, wozu die Vertex-Programme die richtigen Befehle anbieten:

DP3 R8.w, R0, R0;
# R8.w = Länge2
RSQ R8.w, R8.w;
#R8.w=1.0 / sqrt(R8.w)
MUL R8, R0, R8.w;
# R8 = V
		

Nach diesen abge­schlossenen Vor­berechnungen bestimmen Sie den Verlauf des gebrochenen Strahls. Im Folgenden sehen Sie die schrittweise Berechnung der obigen Formel:

# R0 = NdotI
DP3 R0.x, R5, -R8;

# R1.x = 1 - NdotI * NdotI
MAD R1.x, -R0.x, R0.x, c[23].y;

# R1.x = eta2 * (1 - NdotI * NdotI)
MUL R1.x, R1.x, c[22].y;

# R1.x = 1 - eta2 * (1 - NdotI * NdotI)
ADD R1.x, c[23].y, -R1.x;

# R2.x = sqrt(R1.x)
RSQ R2.x, R1.x;

# 1.0 / sqrt(R1.x)
RCP R2.x, R2.x; # sqrt(R1.x)

# R2.x = eta * NdotI + sqrt(R1.x)
MAD R2.x, c[22].x, R0.x, R2.x;

# R2 = N * R2.x
MUL R2, R5, R2.x;

# R2 = eta * I + R2
MAD R2, c[22].x, -R8, R2;
		

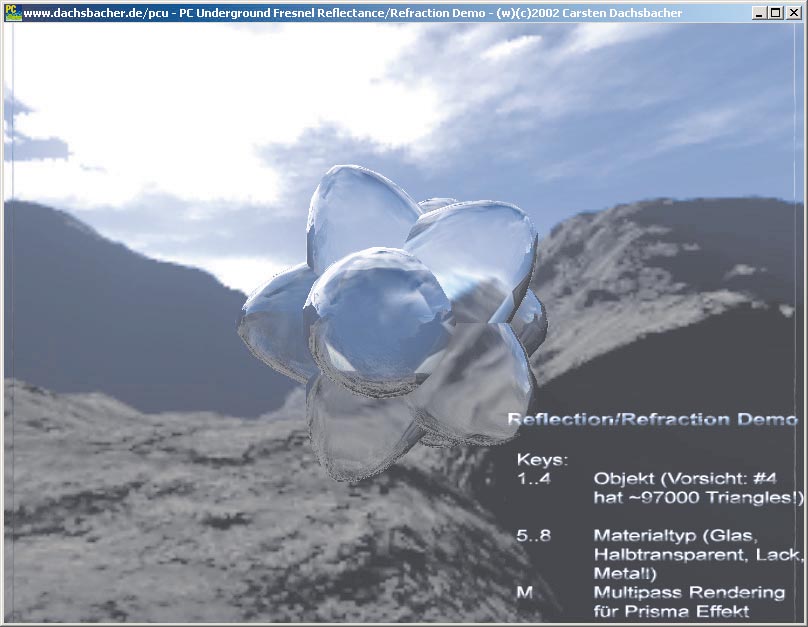
Die Berechnung des gespiegelten Strahls gestaltet sich deutlich einfacher, da Sie nur eine Vektor­skalierung und -addition durchführen müssen:

# R0 = 2N
MUL R0, R5, c[23].z;

# R3 = 2N * NdotI + V
DP3 R4.w, R5, R8;
MAD R3, R4.w, R0, -R8;
		

Jetzt müssen Sie die resultierenden Vektoren R2 und R3 nur noch mit der inversen Kamera-Matrix multiplizieren, um die korrekten Cubemap-Textur-Koordinaten zu erhalten:

DP3 o[TEX0].x, c[12], R2;
DP3 o[TEX0].y, c[13], R2;
DP3 o[TEX0].z, c[14], R2;
DP3 o[TEX1].x, c[12], R3;
DP3 o[TEX1].y, c[13], R3;
DP3 o[TEX1].z, c[14], R3;
		

Die letzte Aufgabe des Vertex-Programms ist die Approximation des Fresnel-Terms. Auch hier verwenden Sie die obige Formel und setzen Sie um:

ADD R4.w, c[23].y,-R4.w;
# 1 - VdotN
MUL R4.w, R4.w, R4.w; # ()2
MUL o[COL0],R4.w, c[21];
# k*(1-VdotN)2
END;
		

Das Vertex-Programm berechnet also aus den Eingabedaten (Vertex­koordinaten und -Normalen) die homogenen Clip­koordinaten, die Textur-Koordinaten und den Fresnel-Term, der in der Primärfarbe (COL0) gespeichert ist.

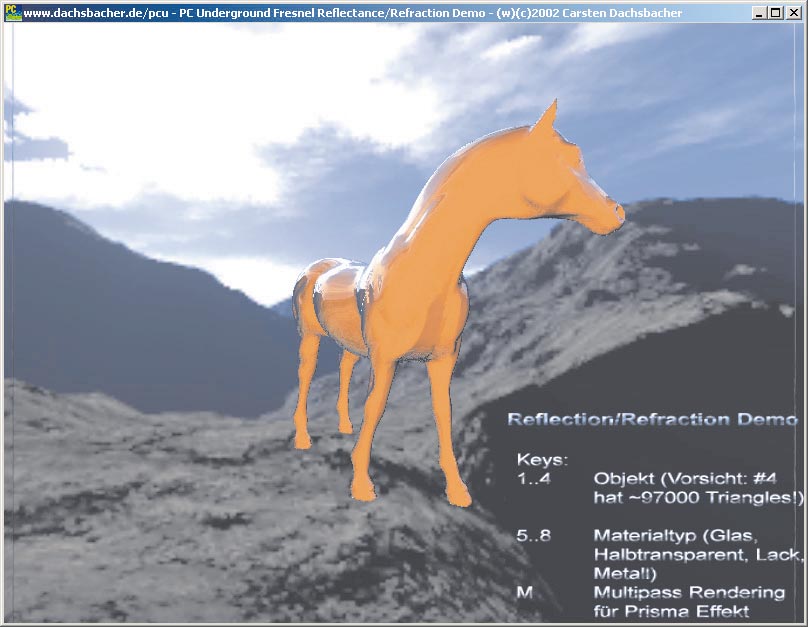
Jetzt gilt es, die berechneten Daten sinnvoll einzusetzen, aus den Farbwerten, den Cubemaps und dem Fresnel-Term die endgültigen Farbwerte zu berechnen. Am einfachsten erledigen Sie diese Aufgabe, wenn Sie die NVParse-Bibliothek für Register Combiners verwenden (Ausgabe 07/02, S. 175).

Es gibt verschiedene Optionen, die Material­eigenschaften zu bestimmen. Die einfachsten Varianten sind entweder eine reine Spiegelung, wie bei metallischen Gegenständen oder eine reine Lichtbrechung. Die dazugehörigen Register Combiners (die den Fresnel-Term nicht verwenden!) sehen wie folgt aus:

// nur Lichtbrechung
nvparse(
	"!!RC1.0 \n"
	"out.rgb = tex0; \n"
);

// Metall
nvparse(
	"!!RC1.0 \n"
	"out.rgb = tex1; \n"
);
		

Wenn Sie einen gläsernen Gegenstand darstellen wollen, bestimmt der Fresnel-Term die Gewichtung der beiden Farben, also eine lineare Kombination:

// color = fresnel * reflect +
// (1-fresnel) * refract
!!RC1.0
{
	rgb
	{
		discard =
			tex0 * unsigned_invert(col0);
		spare0 = tex1 * col0;
		spare1 = sum();
	}
}

out.rgb = spare1;
		

Sie können dem Glas auch eine Eigenfarbe verpassen. Dazu benötigen Sie einen Combiner mehr, mit dem Sie die tex0 Farbe mit einer Konstante mischen:

!!RC1.0
const0 = (0.8, 0.7, 0.4, 1.0);
{
	rgb
	{
		discard = const0;
		spare0 = tex0;
		spare1 = sum();
		scale_by_one_half();
	}
}

{
	rgb
	{
		discard= spare1 * unsigned_invert(col0);
		spare0 = tex1*col0;
		spare1 = sum();
	}
}

out.rgb = spare1;
		

Als letzte Variante hier im Text rendern Sie farbige 3D-Objekte mit einer Fresnel-Spiegelung, indem Sie tex0 durch eine Konstante ersetzen. Alternativ verwenden Sie statt der Cubemap-Textur in der ersten Texture-Stage herkömmliches Textur-Mapping, um den Farbwert zu bestimmen. In diesem Fall passen Sie das Vertex-Programm so an, dass der gebrochene Lichtstrahl nicht berechnet wird. Stattdessen werden die Textur-Koordinaten, die Ihr 3D-Objekt dann mit sich bringt, einfach durchgereicht.

Zusammenbau

Um alle bisher beschriebenen Teile in der Renderloop zusammen­zufassen, muss dies eine bestimmte Abfolge einhalten. Zu Beginn setzen Sie die Kamera­transformation, deren Matrix Sie invertieren müssen. Die inverse Matrix wird vom obigen Vertex-Programm und beim Zeichnen der Skybox benötigt.

glClear(GL_COLOR_ BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();

// Kamera Transformation
glRotatef(...);

//KameraMatrix holen+invertieren
glGetFloatv(GL_MODELVIEW_MATRIX, cameraMatrix);
InverseMatrixAnglePreserving(cameraMatrix,
	cameraMatrixInverse);
		

Dann zeichnen Sie die Skybox, die Sie gleich mit den Cubemaps rendern. Verwenden Sie die Normalen eines 3D-Objektes per OpenGL als Textur-Koordinaten. Damit ersparen Sie sich zusätzlichen Aufwand für das Rendern einer klassischen Skybox. Rendern Sie eine Skysphere, also eine Kugel und keinen Würfel, die aber denselben optischen Effekt wie eine Skybox hat:

// deaktivieren von Vertex RCs und Z-Buffer
glDisable(GL_VERTEX_PROGRAM_NV);
glDisable(GL_REGISTER_COMBINERS_NV);
glDisable(GL_DEPTH_TEST);

// CubemapTexture ->einer Stage
glActiveTextureARB(GL_TEXTURE1_ARB);
glDisable(GL_TEXTURE_CUBE_MAP_ARB);

glActiveTextureARB(GL_TEXTURE0_ARB);
glBindTexture(GL_TEXTURE_CUBE_ MAP_ARB, cubeMap);
glEnable(GL_TEXTURE_CUBE_MAP_ARB);

// Text-koordinate
glTexGeni
//s. Quellcode...
		

Anschließend zeichnen Sie das 3D-Objekt, für das Sie jetzt noch eine beliebige Transformation in der Modelview-Matrix durchführen können. Aktivieren Sie die Cubemaps für die Texturen Stages 0 und 1 und aktualisieren Sie die Textur-Matrix analog zum obigen Code der Skybox bzw. Skysphere. Mit zwei Funktionen können Sie die Parameter für das Vertex Programm, das Brechzahl­verhältnis und die Konstante für die Fresnel-Approximation ändern und anschließend zeichnen Sie das 3D-Objekt.

Unser Beispiel­programm kann 3D-Objekte aus ASCII-Dateien laden. Das Zeichnen erfolgt mit einer zuvor angelegten OpenGL Display List, um relativ performantes Rendering zu erhalten.

void setRefraction(float eta)
//s. Quellcode
void setFresnel(float fresnel)
//s. Quellcode

setFresnel(2.0f);
setRefraction(1.1f);

object->drawObject();
		

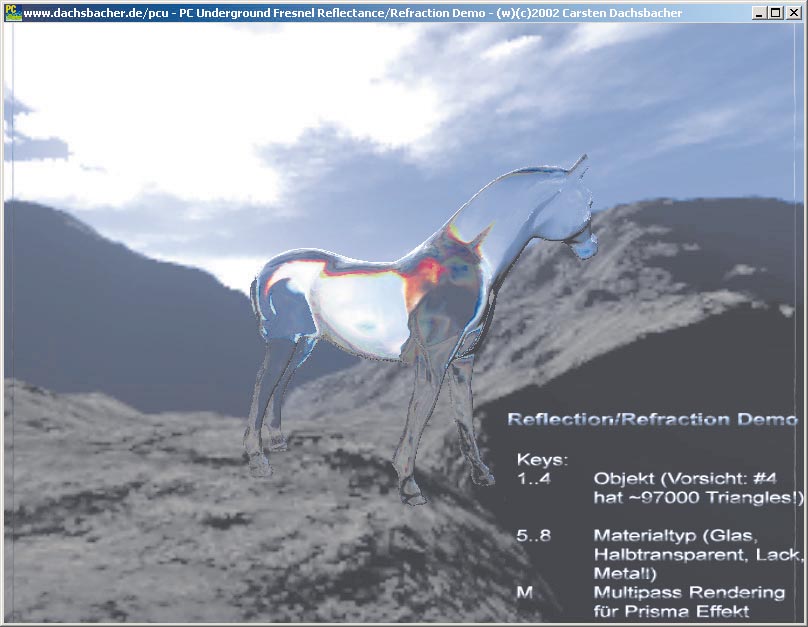
Sie können mit den obigen Funktionen noch weitere wichtige Lichtbrechungs­effekte darstellen. Wenn Sie sich an das Snell’sche Gesetz und die Fresnel-Formel erinnern, fällt auf, dass die Brechzahl von Medien von der Wellenlänge des Lichtes abhängig ist. Vereinfacht betrachtet, setzt sich das Farbbild auf Ihrem Monitor aus Licht von drei Wellenlängen zusammen: Rotes, grünes und blaues Licht deckt bei additiver Farbmischung den Farbraum ab. Sie können das endgültige Bild aus drei einzelnen Renderpasses – für jede Grundfarbe einen – zusammen­setzten.

glDepthFunc(GL_LEQUAL);

// rot
glColorMask(GL_TRUE, GL_FALSE;
	GL_FALSE, GL_FALSE);

setRefraction(1.10f);
object->drawObject();

// grün + blau
//s. Quellcode
		

Für jeden Renderpass können Sie eine eigene Brechzahl festlegen und erhalten Prismeneffekte wie im Bild oben.