Im Strahlenkranz

Carsten Dachsbacher

Trotz der schnell zunehmenden Leistung moderner 3D-Hardware gibt es immer noch zahlreiche Verfechter des Raytracings. Experten arbeiten an Raytracing-Hardware, wobei aus dem Hochschul­bereich wichtige Impulse kommen: http://graphics.cs.uni-sb.de/RTRT/.

Hierbei werden Dreiecke mit Multiprozessor-Rechnern oder Rechen-Clustern dargestellt. Die Vorteile beim Raytracing liegen im einfachen Algorithmus, in der Beherrsch­barkeit von sehr großen 3D-Szenen mit mehreren hundert Millionen Dreiecken und in der vergleichs­weise leichten Programmierung von Oberflächen-Shadern: Damit lassen sich Spiegelungen, Transparenz und Schatten­effekte darstellen. In diesem Artikel lernen Sie die Methoden und Techniken kennen, um auf Ihrem Computer Raytracing-Szenen mit klassischen geometrischen Primitiven wie Ebene, Kugeln und Zylinder zum Leben zu erwecken.

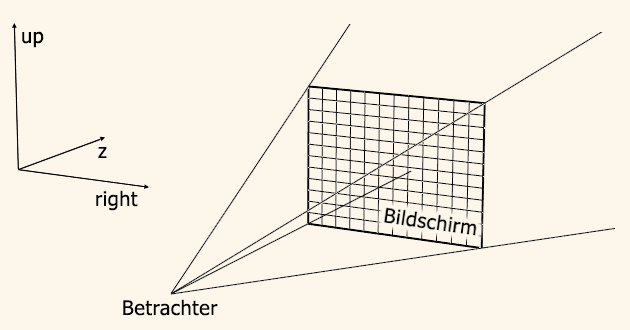
Der klassische Raytracing-Algorithmus ist rekursiver Natur. Er beginnt damit, Strahlen von der Betrachter­position durch den Bildschirm zu schießen, um den Farbwert des Lichts, das aus dieser Richtung zum Betrachter gelangt, zu bestimmen.

Entlang dieser Halbgeraden berechnen Sie die Schnittpunkte mit allen Objekten der Szene und wählen den nächst­liegenden Schnittpunkt zum Betrachter aus. Für einen getroffenen Oberflächen­punkt berechnen Sie eine lokale Beleuchtung wie nach dem Phong-Modell. Lichtquellen der Szene, die andere Objekte verdecken können, sowie Material­eigenschaften beeinflussen die Berechnung. Wenn die Oberfläche spiegelnde Eigenschaften besitzt oder teilweise transparent ist, ruft sich der Raytracing-Algorithmus rekursiv auf, um den Farbbeitrag dieser Lichtstrahlen zu berechnen.

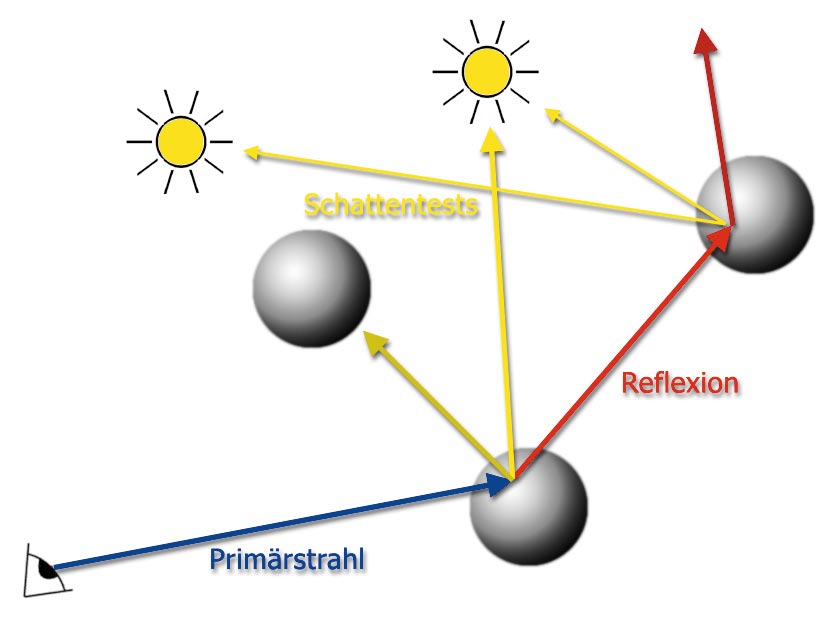
Der Vorteil des Raytracings liegt darin, dass die Beleuchtungs­berechnung und die Spiegelungs- und Transparenz­effekte frei programmierbar sind. Damit erreichen Sie Effekte wie das Bumpmapping mit weniger Aufwand als bei 3D-Grafikkarten.

Wie berechnen Sie die Strahlen, die Sie in die 3D-Szene schießen? Zunächst definieren Sie eine virtuelle Kamera durch ihre Position (pos), den Punkt, auf den sie blickt (to), den Up-Vektor (up) und den Öffnungswinkel (fov). Damit können Sie die Sichtpyramide aus dem ersten Bild aufspannen. Die benötigten Vektoren z, right und up berechnen Sie mit

z = to - from;
right = z x up;
up = z x right;
		

x ist das Kreuzprodukt. Die Vektoren werden anschließend normalisiert, und right- und up-Vektor werden noch mit tan(FOV) bzw. tan(FOV/aspectRatio) skaliert. Ein Strahl vom Betrachter in die 3D-Szene durch den Pixel mit den Koordinaten (x,y) besitzt den Startpunkt pos und die Richtung dir. Mit width und height bezeichnen Sie die Größe des Bildschirms:

dir = z + right *
(2 * x / width - 1.0) + up * (2 * y / height - 1.0);
		

Den Code für die virtuelle Kamera finden Sie in der Datei RTCamera.h auf der Heft-CD. Dort befindet sich auch eine Routine, um die 2D-Position eines Punkts im Raum zu berechnen. Diese ist sehr sinnvoll, weil Sie damit 2D-Bounding-Boxes bestimmen.

Wenn Sie eine Auflösung von 640 x 480 Pixeln in einer Szene mit 20 Objekten verwenden und durch jeden Pixel des Bildschirms einen Strahl schießen, bestimmen Sie mit 640*480*20=6144000 Schnittpunkt­berechnungen nur die zuerst getroffenen Oberflächen. Diese Schnittpunkt­berechnungen der Primärstrahlen lassen sich mehrfach optimieren. Sie können die Zahlen der benötigten Strahlen reduzieren, und Sie können die Schnittpunkt­berechnungen verbessern.

Screen Space Quadtree

Der benötigte Rechenaufwand hängt von der Auflösung des Bildes ab. Nur können Sie die Auflösung nicht beliebig verschlechtern, wenn eine bestimmte Darstellungs­qualität erhalten bleiben soll. Aber Sie können Bereiche des Bilds, in denen kein Objekt oder dieselbe Oberfläche zu sehen ist, gröber abtasten.

Das einfache Prinzip: Beginnen Sie damit, für jeden Block von 8-x-8-Pixeln (oder einer anderen initialen Größe) einen Strahl zu berechnen. Anschließend können Sie feststellen, ob dieser Block eine feinere Abtastung – also mehr berechnete Strahlen – benötigt oder ob die Information ausreicht, um interpolierte Farbwerte zu berechnen. Wenn das der Fall ist, werden die Farbwerte der Ecken des 8-x-8-Blocks interpoliert und keine weiteren Strahlen mehr berechnet.

Jetzt müssen Sie nur eine Lösung finden, damit Sie nicht dieselben Strahlen mehrmals berechnen wie bei der Unterteilung. Weiterhin gilt es, passende Methoden der Unterteilung und Interpolation zu entwickeln. Zunächst soll uns die folgende Struktur genügen, um die Informationen eines berechneten Strahls zu speichern:

typedef struct
{
	U32 flag;
	COLOR lighting;
} TRACEDPOINT;
		

Diese Struktur wird für einen Primärstrahl durch Raytracing ausgefüllt. Außer dem Farbwert speichern Sie im flag-Wert die Information, anhand der Sie entscheiden, ob ein Block weiter unterteilt wird oder ob die Farb­interpolation genügt. Darin sind beispielsweise ein Identifier codiert, der die getroffene Oberfläche repräsentiert, sowie die Information, ob sich der getroffene Oberflächen­punkt im Schatten einer Lichtquelle befindet. Später können Sie diese Struktur erweitern, beispielsweise um diffuse und spekulare Farbwerte, Textur-Koordinaten oder Fogging-Parameter.

Schicken Sie durch jeden Pixel maximal einen Strahl. Dazu legen Sie eine Tabelle mit einem Zeiger für jeden Pixel auf TRACEDPOINT-Strukturen an. Wenn noch kein Strahl für einen Pixel berechnet wird, enthält der entsprechende Eintrag einen NULL-Pointer, sonst einen Zeiger auf die Struktur mit den berechneten Informationen. Um zu vermeiden, dass Sie für jeden Pixel Speicher anfordern müssen, legen Sie sich einen genügend großen Pool von TRACEDPOINT-Strukturen an:

TRACEDPOINT tracedPointPool[X * Y];
TRACEDPOINT *traceHash[ X * Y];
TRACEDPOINT *pool =tracePointPool;
		

Die folgende Methode ruft die rekursive Raytracing-Funktion auf und speichert die entsprechenden Informationen pro Pixel:

void evaluate(int x, int y)
{
	int o = x + y * XRES;
	if(traceHash[o])
		return;

	// new entry
	TRACEDPOINT *n = pool++;
	// Strahl mit Ursprung+Richtung
	RAY ray = ...;
	raytrace(&ray, n, 0, x, y);
	traceHash[o] = n;
}
		

Damit tasten Sie den Bildschirm für jeden Block einmal ab:

for(y=0; y < YRES; y += BLOCKSIZE)
	for(x=0; xflag == p2->flag &&
		p2->flag == p3->flag &&
		p3->flag == p4->flag))
	{
		// Block zum Zeichnen markieren
		return;
	}

U32 hSize = size >> 1;

// einen TRACEDPOINT dazwischen
// bestimmen (durch Raytracing oder Interpolation)
if(p1->flag != p2->flag)
	evaluate(x + hSize, y);
else
	interpolate(p1, p2, x + hSize, y);

// selbiges für p2-p4, p3-p4
// und p1-p3 Kante !
...

// Mittelpunkt durch Raytracing
evaluate(x + hSize,y + hSize);
// rekursiv auf Sub-Blöcke
traceBlock(x, y, hSize);
traceBlock(x + hSize, y, hSize);
traceBlock(x, y + hSize, hSize);
traceBlock(x + hSize, y + hSize, hSize);
		

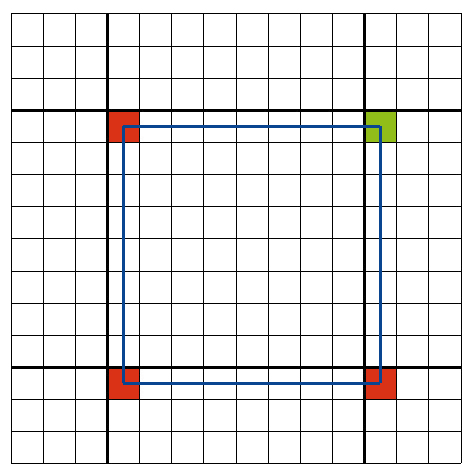
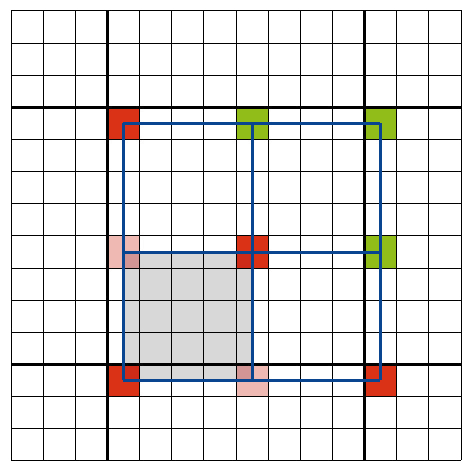
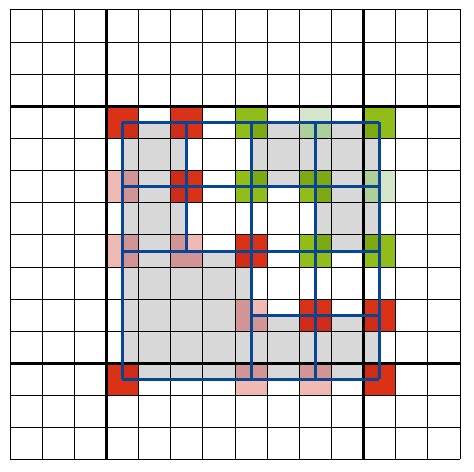
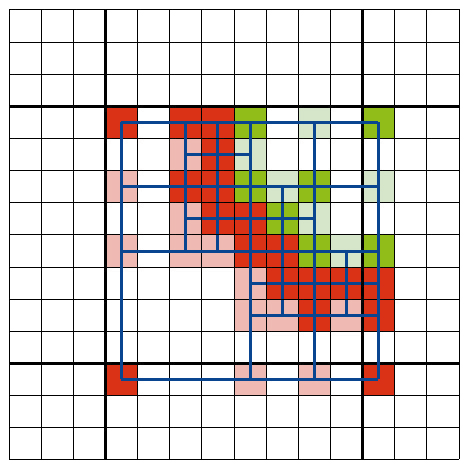
Im obigen Code tauchte eine neue Funktion auf: Alternativ zu evaluate(...) gibt es interpolate(...). Diese Funktion erzeugt aus zwei TRACEDPOINT-Strukturen eine neue Struktur für gegebene Koordinaten durch Interpolation. Des Sinn dahinter ist, weitere Raytracing-Berechnungen einzusparen. Die nächsten vier Bilder verdeutlichen dies.

Dunklere Pixel wurde durch Raytracing berechnet, hellere durch Interpolation, was viel Rechenzeit spart:

void interpolate(TRACEDPOINT *s1,
	TRACEDPOINT *s2, int xd, int yd)
{
	int o = xd + yd * XRES;
	if(traceHash[o])
		return;

	// neuer TRACEDPOINT
	TRACEDPOINT *dst = pool ++;
	dst->flag = s1->flag;
	dst->lighting = (s1->lighting +
		s2->lighting) * 0.5;
	traceHash[o] = dst;
}
		

Raytracing und First Hit Optimization

Die raytrace-Funktion erledigt das komplette rekursive Raytracing. Sie finden den vollständigen dokumentierten Sourcecode auf der Heft-CD. Wichtig bei Echtzeit-Raytracing ist, dass Sie keine Berechnungen unnötig mehrfach ausführen und zeitaufwändige Operationen, wie Vektor­normalisierung oder Normalen­bestimmung, erst berechnen, wenn sie benötigt werden. Da es darum geht, Rechenzeit zu sparen und nicht Speicherplatz, ist es sinnvoll, spezielle Routinen beispielsweise für Schatten­strahlen oder Raytracing bei Rekursions­tiefe 0 (also mit Primärstrahlen) zu schreiben. Diese Aktion verschlingt einen großen Teil der Rechenleistung.

Hier setzt die First Hit Optimization an. Einige Berechnungen wie die Schnittpunkt­berechnung mit Kugeln lassen sich vereinfachen, wenn alle Strahlen vom selben Ursprung – in diesem Fall der Betrachter­position – ausgehen. Solche konstanten Faktoren oder Vektoren berechnen Sie für jedes Objekt der Szene nach einer Änderung der Betrachter­parameter und verwenden diese bei der Schnittpunkt­berechnung mit Primärstrahlen. Ein einfaches Beispiel für solche Konstanten ist der Vektor vom Betrachter zu einem Kugelmittel­punkt und dessen Länge.

Eine weitere sehr sinnvolle Optimierung für den First Hit Case sehen Sie im nächsten Bild. Sie können für die meisten geometrischen Primitive, wie Kugel, Kegel oder Quader eine 2D-Bounding-Box berechnen. Das ist ein Rechteck auf dem Bildschirm (begrenzt durch die linke obere und rechte untere Ecke), das den Bereich möglichst eng umschließt, in dem ein Objekt zu sehen ist. Bevor Sie also für einen Pixel und ein Objekt einen Schnittpunkt testen, prüfen Sie, ob der Pixel innerhalb der Bounding Box liegt.

Der Raytracing Code befindet sich in der Sourcecode-Datei raytrace.cpp. Die geometrischen Primitive sind von der Klasse RTObject (RTObject.h) abgeleitet. Ihre optimierten Schnittpunkt-, Bounding-Box-Berechnungen und Vorberechnungs­routinen befinden sich in RTPlane.cpp/h, RTSphere.cpp/h und in RTBox.cpp/h.

Shadow Cache

Beim Shadow Cache handelt es sich um eine sehr einfache Optimierung. Sehr aufwändig sind beim Raytracing die Schattentests, denn für jeden Schnittpunkt mit einer Oberfläche müssen Sie die Anzahl der Objekte mit der Anzahl der Lichtquellen multiplizieren. Dies können Sie etwas optimieren, weil nicht interessant ist, welches Objekt getroffen wird, sondern nur, ob irgendeins die Lichtquelle verdeckt.

Aber es geht noch besser. Der Trick beim Shadow Cache: Wurde der Schattenstrahl eines zuletzt getroffenen Oberflächen­punkts zu einer Lichtquelle von Objekt A abgeblockt, wird beim nächsten Schattentest dieser Lichtquelle wieder zuerst überprüft, ob Objekt A den Schattenstrahl schneidet. Für jede Lichtquelle speichern Sie einen Zeiger auf ein Objekt. Bei einem Schattentest für diese Lichtquelle testen Sie zuerst, ob sich der Schattenstrahl mit diesem Objekt schneidet.

Existiert ein Schnittpunkt, sind Sie mit nur einer Schnittpunkt­berechnung fertig. Existiert dieser nicht, müssen Sie die Strahlen auf Schnittpunkte mit anderen Objekten untersuchen. Wurde ein anderes geschnitten, wird der Shadow-Cache-Zeiger der Lichtquelle auf dieses Objekt gesetzt.

OpenGL

Was hat OpenGL mit Raytracing zu tun? Mit OpenGL können Sie die Blöcke, die Sie durch das Raytracing bzw. das Unterteilen der Blöcke erhalten haben, schnell zeichnen. Das Zeichnen könnten Sie auch per Software erledigen, aber wenn Sie die Vertex-Daten geschickt generieren, ist die OpenGL-Variante mit Hardware-Unterstützung deutlich schneller. Als Vertex-Daten benötigen Sie zum einen die Eckpunkte der Blöcke, zum anderen die dazugehörigen Farbwerte. Für das Rendering verwenden Sie am besten die OpenGL Vertex und Color Arrays und zeichnen mit glDrawElements(...). Die Daten umfassen dann je zwei Integer-Werte als Koordinaten und zwei Float-Werte für die Farb­information pro Eckpunkt:

U32 *pVertexArray = new U32[XRES * YRES * 2];
VERTEX3D *pColorArray = new VERTEX3D[...];
		

Jetzt erweitern Sie die evaluate(...)- und interpolate(...)-Funktion so, dass immer, wenn eine neue TRACEDPOINT-Struktur angelegt wird, ein neuer Vertex an die obigen Listen angehängt wird:

...
pVertexArray[nVertices * 2 + 0] = x;
pVertexArray[nVertices * 2 + 1] = y;
pColorArray[nVertices] = n->lighting;
...
		

Außerdem müssen Sie für jede Bildschirm­koordinate den Index des dazugehörigen Eckpunkts wissen. Dazu verwenden Sie ein weiteres Array:

// init
U32 *indexTable = new U32[XRES * YRES];

// in evaluate und interpolate:
...
indexTable[o] = nVertices;
nVertices++;
...
		

Jetzt gilt es noch, die Indizes zu generieren, die Sie für das Rendering benötigen. Je vier Indizes stellen die Eckpunkte eines Blocks dar. Diese Indizes generieren Sie in der traceBlock-Funktion. Im obigen Code-Auszug dieser Funktion befindet sich bereits der Kommentar, der die entsprechende Stelle markiert. Hier speichern Sie die vier Indizes, die Sie für jeden der Eckpunkte aus der indexTable lesen. Sie speichern die Folge der Indizes in einem separaten Array, um alle Blöcke mit einem OpenGL-Funktions­aufruf zu zeichnen.

U32 nBlockIndex = 0;
U32*pBlockIndex = new U32[XRES * YRES * 4];
...
pBlockIndex[nBlockIndex++] =
	indexTable[ofs1];

pBlockIndex[nBlockIndex++] =
	indexTable[ofs2];

pBlockIndex[nBlockIndex++] =
	indexTable[ofs4];

pBlockIndex[nBlockIndex++] =
	indexTable[ofs3];
		

Damit haben Sie eine sehr elegante und performante Lösung, um den OpenGL-Output zu erzeugen. Das Rendering erfolgt mit den Aufrufen:

glVertexPointer(2, GL_INT, 0, pVertexArray);
glColorPointer(3, GL_FLOAT, 0, pColorArray);

glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);

glDrawElements(GL_QUADS, nBlockIndex,
	GL_UNSIGNED_INT, pBlockIndex);

glDisableClientState(GL_COLOR_ARRAY);
glDisableClientState(GL_VERTEX_ARRAY);
		

Der Code, um die Blöcke rekursiv zu teilen und zu zeichnen, befindet sich in der Datei quadtree.cpp/h.