Tiefenrausch

Carsten Dachsbacher

In der Computergrafik, allgemein in zwei­dimensionalen Bildern, spielen eine Reihe von Aspekten eine wichtige Rolle, um einen räumlichen Eindruck der Szene zu vermitteln. Dazu zählt zum Beispiel die Perspektive, d.h. weiter entfernte Objekte nehmen auf der Bildebene weniger Fläche ein als nähere sowie parallele Linien, die in großer Distanz konvergieren. Auch Licht und Schatten spielen eine wichtige Rolle. Erst durch die unterschied­liche Beleuchtung einer gekrümmten Fläche wird diese auch gut als solche wahrgenommen. Schatten verdeutlichen vor allem die relative Lage verschiedener Gegenstände. Weitere Aspekte sind mit der Entfernung abnehmende Details, Verdeckung von weiter entfernten Objekten und relative Bewegungs­geschwindigkeit in animierten Szenen.

Eine wichtige Eigenschaft kann ein zwei­dimensionales Bild nicht enthalten: Ein Mensch kann beim Betrachten einer Szene nicht zwei unterschied­liche Bilder wahrnehmen. Die beiden Augen besitzen einen Abstand (den interokularen Abstand), der zu unterschied­lichen Projektionen der wahrgenommenen Szene auf der Netzhaut, also zu unterschied­lichen Bildern führt. Dies wird auch mit Binocular Disparity bezeichnet und ist der wichtigste Punkt für einen räumlichen Eindruck. Trotzdem können falsche Darstellungen der anderen Aspekte störend wirken. Für das 3D Stereo Rendering ist es also unerlässlich, zwei Bilder zu generieren, die – von je einem Auge – so wahrgenommen werden können, dass ein räumlicher Eindruck entsteht. Der menschliche Sehapparat muss die Bilder als eines akzeptieren und die Tiefen­information wie gewünscht verarbeiten. Werden die Bilder nicht als eines wahrgenommen, kann einer der folgenden vier Fälle eintreten:
● Für ein Auge wird ein Bild dominant und dieses vorrangig wahrgenommen.
● Die Tiefen­wahrnehmung wird übertrieben und damit zu schwach.
● Das Betrachten der Szene ist unbehaglich.
● Der Betrachter sieht zwei separate Bilder.

Um das Stereo Rendering einzusetzen, stehen verschiedene Techniken zur Verfügung. Die bekanntesten sind die so genannten Shutter-Brillen. Hierbei werden auf dem Monitor abwechselnd die Bilder für das linke bzw. rechte Auge dargestellt, wobei durch die Brille mit Hilfe von LCD-Shuttern jeweils die Sicht für ein Auge blockiert wird. Einige 3D-Grafikkarten unterstützen diese Technik. Allerdings werden sehr hohe Bildwiederhol­frequenzen benötigt, um eine flimmerfreie Darstellung zu erhalten. Die wohl teuerste Technik sind Polarisations­brillen. Hierbei wird auf einer Leinwand das Bild für jeweils ein Auge von einem Projektor dargestellt.

Allerdings besitzt das Licht jedes Projektors eine unterschied­liche Polarisation. Durch eine Polarisations­brille können Sie die beiden Bilder getrennt wahrnehmen. Beide Verfahren können farbige Bilder darstellen. Um als einfachste Methode daheim Stereo Rendering zu erfahren, verwenden Sie Rot-Grün- oder Rot-Blau-Brillen. Hierbei werden die beiden Bilder gleichzeitig auf dem Monitor dargestellt. Das Bild für das linke Auge in rot, gemischt mit dem Bild für das rechte Auge in blau oder grün. Die eingefärbten Brillengläser separieren die Bilder, wobei allerdings Farben nicht mehr korrekt dargestellt werden. Das Beispiel­programm dieser Ausgabe erzeugt solche Bilder, die Sie mit einer solchen einfachen Brille betrachten können. Diese können Sie schon für weit unter einem Euro im Internet bestellen und in 3D sehen. Suchen Sie unter www.google.de nach dem Begriff rotblau 3d brillen.

Parallaxe

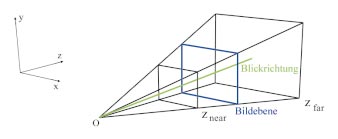
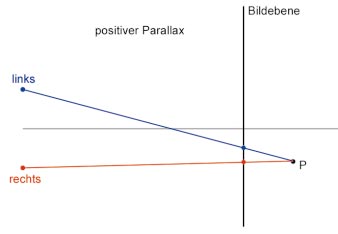
Bevor Sie sich auf die Implementation stürzen, beschäftigen wir uns mit der Theorie. Im Bild View Frustum sehen Sie die Computergrafik dazu. Das Frustum ist der Teil der mathematischen Welt, der durch die virtuelle Kamera sichtbar ist. Dieser Teil hat die Form eines Pyramiden­stumpfes, wenn Sie eine perspektivische Abbildung verwenden. Betrachten Sie das anschließende Bild: Hier sehen Sie in Aufsicht den Fall eines hinter der Projection Plane (also dem Bildschirm) liegenden Punktes. Die Projektion dieses Punktes für das linke und rechte Auge befindet sich an unterschied­lichen Stellen der Bildebene. Dieser Abstand wird als horizontaler Parallax bezeichnet.

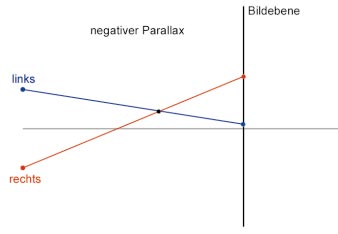
Da sich die Projektion für das linke Auge auf der linken Seite befindet (und umgekehrt für das rechte Auge), wird der Abstand als positiver Parallax definiert. Der maximale horizontale Parallax ist gleich dem Abstand der Augen und tritt auf, wenn der Objektpunkt unendlichweit entfernt ist. Ist der Punkt – wie im nächsten Bild – vor der Bildebene, so ist die Projektion für das linke Auge weiter rechts als die Projektion des Punktes für das rechte Auge, was als negativer horizontaler Parallax bezeichnet wird. Dieser ist betragsmäßig gleich dem interokularen Abstand, wenn sich der Punkt genau zwischen Betrachter und Bildebene befindet. Er kann unendlich groß werden.

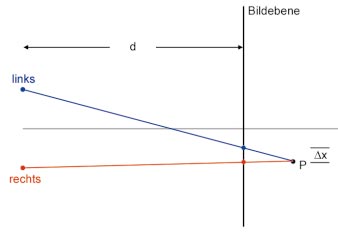
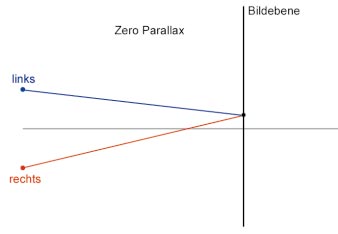
Im folgenden Bild sehen Sie, dass ein Punkt auf der Bildebene liegt. Dann ist die Parallaxe gleich Null. Die unterschied­lichen Fälle finden Sie in der Tabelle Horizontaler Parallax. Für den horizontalen Parallax H eines Punktes P lassen sich folgende Fälle unterscheiden (d ist der interokular Abstand). Für den Parallax Winkel gilt:
T > 0: P liegt hinter und
T <0: P liegt vor der Bildebene.

Objekte, die sich vor der Bildebene befinden, scheinen beim Stereo Rendering auch vor dem Monitor zu sein. Objekte hinter der Bildebene erwecken den Eindruck, im Monitor zu liegen.

Im Allgemeinen ist es einfacher, Stereo-Bildpaare zu betrachten, bei denen die Objekte hinter der Bildebene liegen. Dies können Sie durch die flexible Anpassung der Kamera­parameter – wie in den nächsten Abschnitten vorgeführt – erreichen. Dabei gibt es einige Aspekte und Faustregeln, die Sie beachten sollten. Die Stärke des Stereo Effektes hängt sowohl vom Abstand des Betrachters zur Bildebene, als auch dem Abstand der beiden Kameras ab. Ein zu großer Abstand erzeugt so genannte Hyperstereo Effekte und führt leicht zu schlechter Wahrnehmung des 3D-Bildes.

Als Richtwert für die maximale Trennung der Bilder verwenden Sie am besten fünf Prozent des Abstands zur Bildebene. Die zweite Regel besagt, dass der negative (horizontale) Parallax betragsmäßig nicht den interokularen Abstand überschreiten sollte.

Die letzte Regel zieht den so genannten Parallax Winkel T heran. Dieser ist definiert, als

T = 2 * arctan(∆ x / (2d)),
		

wobei ∆x der horizontale Parallax eines projizierten Punktes und d der Abstand des Betrachters von der Bildebene ist. Für alle Punkte der 3D-Szene sollte der Wert von T 1.5 Grad nicht überschreiten. Die verschiedenen Fälle für T finden Sie in der Tabelle Vergleich Toe-In / Off-Axis. Meistens wird für die Grenze von T im Negativen ein Wert nahe Null gewählt, um den negativen horizontalen Parallax, der im Allgemeinen schwerer bei der Betrachtung zu verarbeiten ist, zu beschränken.

Toe-In-Methode

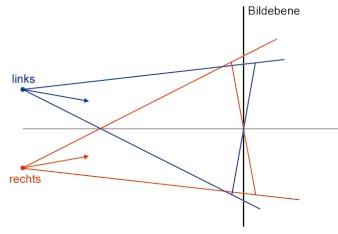
Von den verschiedenen Methoden, um Stereo-Bildpaare zu rendern, lernen Sie hier zwei kennen. Die erste ist die so genannte Toe-In-Methode, die sehr weit verbreitet ist. Allerdings liefert die Technik keine korrekte Darstellung. Sie berechnen dazu zwei Bilder, indem Sie zwei virtuelle Kameras, mit identischem Öffnungswinkel, an die Stelle der Augen platzieren. Diese Kameras besitzen einen gemeinsamen Zielpunkt, den Mittelpunkt der Projektions­ebene.

Das Bild verdeutlicht diesen Sachverhalt, der im Wesentlichen einer Rotation der 3D-Szene entspricht. So erzeugte Stereo-Bildpaare vermitteln zwar einen räumlichen Eindruck, aber verursachen bei längerer Betrachtung verstärkt Unbehag­lichkeit. Der Grund hierfür ist eine auftretende vertikale Parallaxe : Die Projektionen des Punktes P im Bild Toe-In-Methode sind nicht nur parallel zur Bildebene verschoben, sondern auch vertikal, also eine Verschiebung aus der Bildebene heraus! Besonders stark ist dieser Effekt bei größeren Öffnungs­winkeln.

Hinzu kommt ein weiterer Nachteil: Solche Stereo-Bildpaare sind jeweils immer für einen Betrachter­standpunkt berechnet, der meist als mittig vor dem Bildschirm angenommen wird. Bei einem anderen Standpunkt, der bei teuren Systemen z.B. mittels eines Tracking-Verfahrens ständig neu bestimmt wird, treten mit dem Toe-In-Verfahren Verzerrungen auf.

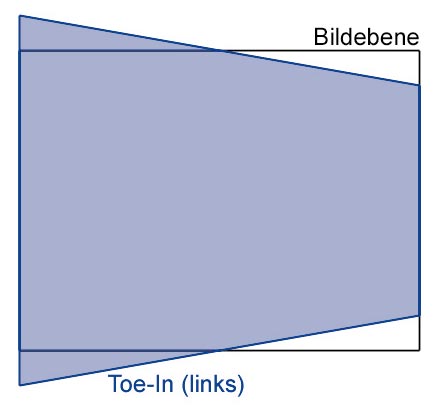
Die Grafik Toe-In (links) verdeutlich, wie sich der auf der Bildebene gedachte, rechteckige Bildschirm auf das gerenderte Bild auswirkt. Diese Verzerrung ist nur bei einem mittig platziertem Betrachter akzeptabel!

Dafür lässt sich diese Methode einfach programmieren. Sie setzen zwei identische Kameras an die Position der Augen, die Sie auf einen gemeinsamen Zielpunkt blicken lassen. Das erreichen Sie prinzipiell mit den folgenden OpenGL-Kommandos:

// Projektionsmatrix
glMatrixMode(GL_PROJECTION);...

// linkes Auge
glMatrixMode(GL_MODELVIEW); ...

// rechtes Auge
glLoadIdentity(); ...
		

Off-Axis

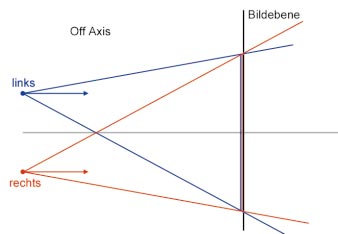
Die so genannte Off-Axis-Methode stellt die korrekte Art dar, um Stereo-Bildpaare zu rendern. Dabei tritt kein vertikaler Parallax auf, was zur Folge hat, dass sich solche Bilder entspannter betrachten lassen. Dazu benötigen Sie asymmetrische Kamera-Frusta, wie Sie in der Aufsicht im Bild Off Axis entnehmen können.

Solche Kamera-Frusta entstehen durch Scherung. Sie können sie auch mit OpenGL verwenden, wobei allerdings der gluPerspective(...)-Befehl nicht mehr ausreicht. Solche Frusta müssen Sie selbst mit dem glFrustum(...)-Befehl aufbauen, was wir Ihnen im Folgenden vorführen. Ein weiterer Vorteil der Off-Axis-Methode ist, dass die erzeugten Bilder auch dann korrekt sind, wenn sich der Betrachter nicht mittig vor dem Bildschirm befindet, da ein gedachtes Rechteck auf der Bildebene immer als solches auf den Bildschirm abgebildet wird. Die Betrachter­position muss natürlich bekannt sein. Sie kann – wie bereits erwähnt – mittels optischer oder magnetischer Tracking-Systeme bestimmt werden.

Die Berechnung der gescherten asymmetrischen Frusta ist allerdings nicht so kompliziert, wie Sie vielleicht befürchten. Betrachten Sie dazu zunächst den glFrustum(...)-Befehl:

void glFrustum (GLdouble left, GLdouble right,...
		

Dieser Befehl erzeugt eine 4x4-Matrix mit einer perspektivischen Abbildung. Die Punkte (left, bottom, znear) und (right, top, znear) bestimmen die linke untere, bzw. rechte obere Eck des Rechtecks auf der Z-Near-Ebene, das auf den Bildschirm abgebildet wird. Das geschieht unter der Annahme, dass sich der Betrachter an der Position (0,0,0) befindet. Die znear bzw. zfar-Parameter, die beide größer als Null sein müssen, geben den Abstand zur Z-Near und Z-Far-Ebene an. Für die Berechnung der Kamera-Frusta verwenden Sie folgende Bezeichnungen:
w/h: Breite bzw. Höhe des Bildschirms
d: Abstand des Betrachters zur Bildebene
o: Interokular Abstand
zn, zf: Abstand zur Z-Near- bzw. Z-Far-Ebene

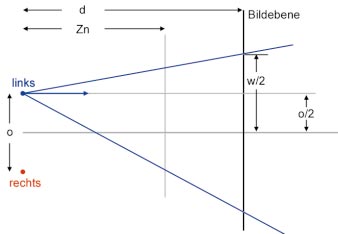
Das Kamera-Frustum für das linke Auge befindet sich um d/2 nach links verschoben (relativ zur Betrachter­position). Somit besitzt die linke Seite eine Breite von (w/2 - d/2). Die left-Koordinate (die negativ ist!), erhalten Sie durch Projektion dieses Wertes auf die Z-Near-Ebene:

left = - (w/2-d/2)* zn / d;
		

Analog dazu, besitzt die rechte Seite eine Breite von (w/2 + d/2):

right = (w/2+d/2) * zn / d;
		

In der Vertikalen ist das Kamera-Frustum symmetrisch und jeweils (h/2) hoch, beachten Sie auch hierbei die Vorzeichen:

top = - h/2 * zn / d;
bottom = - h/2 * zn / d;
		

Die Übergabe der Parameter an OpenGL erfolgt dann mit:

glMatrixMode(GL_PROJECTION);
		

Jetzt müssen Sie vor dem Rendering der 3D-Szene für das linke Auge noch die Verschiebung der Kamera berechnen, denn das linke Auge befindet sich um o/2 zur Betrachter­position verschoben. Diese Translation nehmen Sie am besten in der Modelview Matrix vor:

glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef (o/2.0f, 0.0f, 0.0f);
		

Alle weiteren Trans­formationen, wie z.B. die Positionierung des Betrachters mit gluLookAt(...) oder Objekt­transformationen können Sie wie gewohnt anwenden. Für das rechte Auge führen Sie die Berechnung des Frustums analog durch, wie Sie es für das linke Auge schon erprobt haben. Wie gewohnt finden Sie alles im Beispiel­programm zu dieser Ausgabe.

Rendering in OpenGL

Um das Stereo-Bildpaar darzustellen, verwenden Sie – wie bereits erwähnt – am einfachsten eine Rot-Blau- oder Rot-Grün-Darstellung. Diese können Sie in OpenGL (auch in anderen APIs wie Direct3D) erreichen. Zunächst löschen Sie wie üblich den Frame-Buffer (in schwarz) und den Z-Buffer:

glClearColor(0.0, 0.0, 0.0, 1.0);
glClear(GL_COLOR_BUFFER_BIT |
	GL_DEPTH_BUFFER_BIT);
		

Dann berechnen Sie die Kamera­parameter für das linke Auge und setzen die OpenGL-Matrizen. Bevor Sie jetzt die 3D-Szene rendern, beschränken Sie den Schreibzugriff auf den Frame-Buffer auf den Rot-Kanal:

glColorMask(GL_TRUE, GL_FALSE,
	GL_FALSE, GL_FALSE);
		

Um nun das Bild für das rechte Auge darzustellen, müssen Sie nur den Z-Buffer löschen, um die Szene korrekt rendern zu können. Den Frame-Buffer löschen Sie nicht, sondern beschränken den Schreibzugriff auf blau, grün oder blau/grün (cyan), je nach verwendeter Stereobrille:

glClear(GL_DEPTH_BUFFER_BIT);
switch (brille)...
renderScene();
		

Klippen des Stereo Renderings

Eine Reihe von Techniken bedürfen Beachtung, wenn Sie diese mit Stereo Rendering kombinieren wollen. Die Schwierig­keiten beginnen beim Gouraud Shading. Beim Gouraud Shading berechnen Sie, kurz formuliert, die Beleuchtung für Dreiecksnetze nur an den Eckpunkten der Dreiecke und Sie interpolieren die berechnete Helligkeit linear über das Dreieck.

Ebenso verfahren Sie beim normalen Rendering wie mit glShadeModel(GL_SMOOTH). Beim Gouraud Shading treten zwei Artefakte auf (auch beim Nicht-Stereo-Rendering), die so genannten Mach-Band-Effekte, die die Dreieckskanten sichtbar machen, sowie verschwindende Glanzlichter. Der Aspekt ist wichtig. Um Glanzlichter korrekt darzustellen, berechnen Sie eine Beleuchtung pro Pixel – eine Interpolation berechneter Helligkeiten genügt nicht. Da aber der Betrachter­standpunkt für die beiden Bilder (Augen) unterschied­lich ist, können Glanzlichter auf einem Bild verschwinden, während sie auf dem anderen noch gut erkennbar sind. Solche Unterschiede stören.

Ein weiterer Aspekt, der auch wiederum mit den unterschied­lichen Betrachter­positionen der Augen zusammenhängt, ist eine Level-of-Detail-Darstellung von Dreiecksnetzen. Diese unterschied­lichen Positionen können zu unterschied­lichen Geometrien/LOD-Stufen führen, wenn Sie nicht darauf achten, beispielsweise eine gemeinsame Referenz­position für solche Berechnungen zu verwenden.

Der letzte hier erwähnte Punkt ist das Bump-Mapping. Hierbei wird die Oberflächen­normale pro Pixel für die Beleuchtungs­berechnung pertubiert (modifiziert). Dadurch vermitteln Sie den Eindruck einer gewellten oder gewölbten Oberfläche. Die Oberfläche selbst wird aber nicht verschoben. Beim Stereo Rendering wird die Oberfläche zwar von jedem Auge als gewellt wahrgenommen, aber die Oberflächen­punkte befinden sich nach wie vor auf einer Ebene. Dieses Problem erkennen Sie aber nur bei sehr starken Pertubationen und guten Stereo Systemen – mit einer Farb-Stereo Brille sollten Sie solche Artefakte kaum erkennen können.