Komplexe Objekte

Carsten Dachsbacher

Das Normal-Mapping ist eine Technik, mit der Sie die Low-Polygon-3D-Modelle so beleuchten können, dass sie wie deutlich höher aufgelöste Dreiecksnetze aussehen. Dabei speichert eine Textur für jeden Oberflächen­punkt der Low-Polygon-Variante die Normale als Farbwert codiert, die dem detaillierten Dreiecksnetz an dieser Stelle entspricht.

Das Ziel ist also das gleiche, das Sie vom üblichen Bump Mapping kennen: Das Rendering durch eine modifizierte Normale für die Beleuchtungs­berechnung soll detaillierter beeindrucken, als die Geometrie des Dreiecksnetzes tatsächlich vorgibt. Solche Normal-Maps können Sie automatisch berechnen lassen, wenn Sie eine niedrig und eine hoch aufgelöste Variante eines Dreiecksnetzes vorliegen haben. Das Programm Normal Mapper, das Sie dazu benötigen, können Sie von der ATI Developer Homepage downloaden: www.ati.com/developer/NormalMapper_3_1.zip.

Es gibt auch noch weitere Programme dieser Art, wie Polybump von Crytek (www.crytek.de) oder Open Render Bump von Soclab (www.soclab.bth.se/practices/orb.html). Diese Ausgabe verwendet das ATI-Tool.

Das Prinzip

Wie bereits erwähnt, berechnen diese Tools für jeden Oberflächen­punkt des niedrig aufgelösten Dreiecksnetzes die Normale, die das besser aufgelöste Netz an der entsprechenden Stelle der Oberfläche hat. Um diese Information zu speichern, benötigen Sie als erstes eine Para­metrisierung (auch UV Mapping genannt) für eine Normal Map (also eine Textur). Die Textur-Koordinaten der Dreiecke für die Normal Map müssen so gewählt sein, dass sich keine Dreiecke – in der Textur – überschneiden. Solche Textur-Koordinaten zuzuweisen, ist von Hand viel zu aufwändig und für komplexe Objekte schlichtweg unmöglich, deshalb bieten Modelling Tools, wie Maya oder 3D-Studio Max, die entsprechende Funktionalität – entweder direkt als Bestandteil der Software oder per Plug-in. Sollten Sie keines dieser Tools zur Verfügung haben, empfehlen wir Ihnen als Startpunkt für eine eigene Implementation die Webpage www.realistic3d.com/ von K. Hurley, der Source Code für ein solches 3D-Studio Max Plug-in zum Download anbietet. Eine weitere sehr gute Quelle ist die Homepage von C. Bloom (www.cbloom.com/).

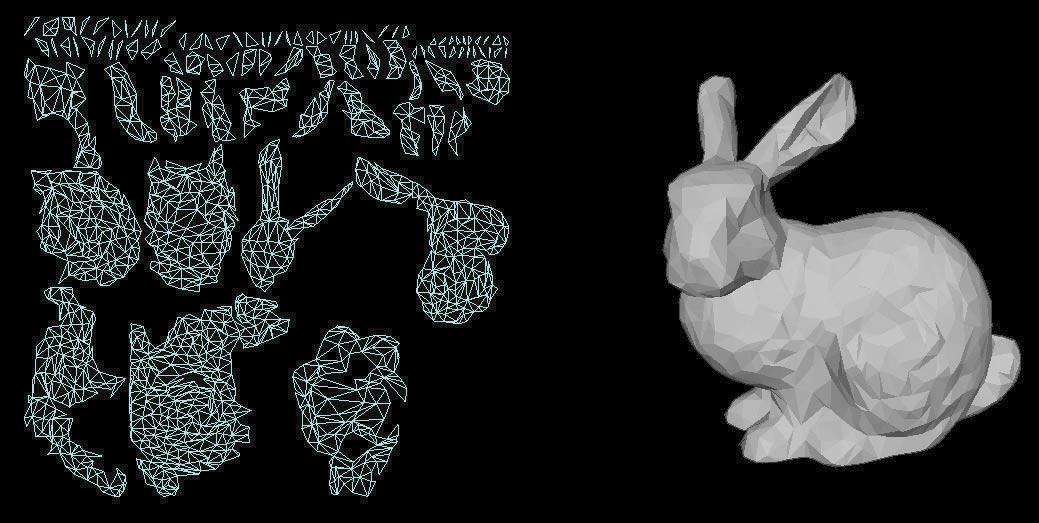
Das Bild zeigt eine geeignete UV-Para­metrisierung. Damit entspricht nun jeder Punkt der Textur keinem oder genau einem Punkt auf der Objekt­oberfläche.

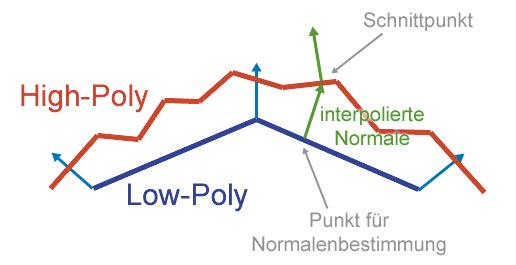
Das Normal Mapper Tool geht wie folgt vor: Es zeichnet die Dreiecke des Low-Polygon-Modells entsprechend ihrer Textur-Koordinaten in die Normal Map. Für jeden Texel wird der dazugehörige Punkt auf der Oberfläche und die interpolierte Normale (jeweils der Low-Polygon Modells) bestimmt. Anschließend berechnen Sie mit dem High-Polygon-Modell die Schnittpunkte des Strahls, gegeben durch den Oberflächen­punkt und die Normale. Anhand des Schnittpunkts lässt sich die dazugehörige Normale bestimmen, die dann in der Normal Map gespeichert wird.

Bei mehreren Schnittpunkten gibt es verschiedene Heuristiken, welcher der Schnittpunkte als Kriterium herangezogen wird. Die Dreiecksnetze übergeben Sie dem ATI Normal Mapper jeweils im nmf-Format, das Sie wiederum mit Plug-ins aus Maya und 3D-Studio Max exportieren können, oder auch mit dem Dreams3D Model Editor (www.sibvrv.km.ru/products/svd3d.htm). Weitere Informationen zum nmf-Format finden Sie im Kasten.

Object versus Tangent Space

Beim Bump Mapping unterscheiden Sie prinzipiell zwischen zwei verschiedenen Ansätzen. Der erste, den Sie bereits aus früheren PC-Underground-Artikeln kennen, ist das so genannte Tangent Space Bump Mapping.

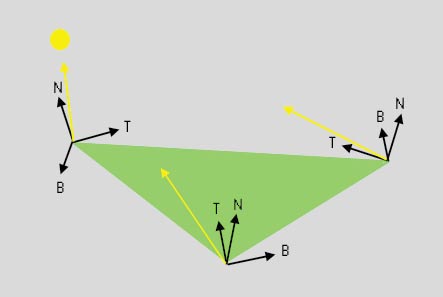
Dabei definieren Sie für jeden Vertex ein Koordinaten­system (den Tangent Space), den Normale, Binormale und Tangente bilden. Eine entsprechende Bump Map speichert die Normalen relativ zu diesem Koordinaten­system, d.h. eine Normale, die entlang der Normale des Tangent Space zeigt, ist in der Bump Map als Vektor (0, 0, 1)T definiert. Diese Technik ist relativ Textur sparend und erlaubt beliebige Textur Mappings. Allerdings müssen Sie dafür im Vertex Shader einige Vorbe­rechnungen durchführen.

Den anderen Ansatz gestalten Sie mit dem UV-Mapping. Da Sie jedem Punkt der Oberfläche genau einen Teil der Textur zuweisen, können Sie direkt die Normale im Object Space (also relativ zu den Koordinaten der Vertices) speichern. Dadurch vermeiden Sie etwas Aufwand bei den Vertex Shadern, da Sie nur einmalig innerhalb der Applikation die Lichtquelle in den Object Space transformieren müssen, und außerdem einige Artefakte, die bei Tangent Space Bump Mapping in Zusammenhang mit bestimmten UV-Mappings auftreten können. Im Bild sehen Sie den – in der Computergrafik – berühmten Stanford Bunny, der auf etwa 4 800 Dreiecke und die entsprechende Normal Map reduziert ist. Die Normal Map wurde mithilfe des voll aufgelösten Dreiecksnetzes mit knapp 70 000 Dreiecken gebildet. Die Normalen sehen Sie rechts im Bild als Farbe codiert, wobei sich kaum noch Unterschiede zum original Datensatz ausmachen lassen. Das Bild auf Seite XXX zeigt ein weiteres bekanntes Modell: Der Drache wurde ebenfalls auf 3 500 Dreiecke reduziert, doch das Rendering mit den Normal Maps lässt kaum Wünsche offen.

Normal Maps erzeugen

Nach dem wir Ihnen nun das Prinzip verdeutlicht und hoffentlich schmackhaft gemacht haben, zeigen wir Ihnen jetzt, wie Sie es Schritt für Schritt selbst durchführen. Der Normal Mapper ist ein Kommandozeilen-Tool, dem Sie die Dateinamen der Low- und High-Polygon-Variante des 3D-Objektes übergeben:

normalmapper w lowpoly.nmf highpoly.nmf
	512 512 normalmap.tga
		

Den Parameter w geben Sie an, um Object Space Normal Maps zu generieren, die restlichen Parameter bezeichnen die Größe und den Dateinamen der Textur. Typischerweise gestalten Sie in einem Modelling­programm zunächst die detaillierte Version des 3D-Modells.

Die niedriger aufgelöste Variante erhalten Sie entweder durch automatische Dreiecksnetz Reduzierer (enthalten im Modelling Paket oder bei http://lodbook.com/) oder durch Handarbeit. Bei Computer­spielen investieren die Programmierer meist viel Handarbeit, da dies bessere Ergebnisse erzielt.

Um Ihnen weitere Konvertier­arbeit zu ersparen, finden Sie auf der CD zu dieser Ausgabe ein Konverter-Tool von dem nmf in das obj-Dateiformat, das unser Direct3D-Beispiel­programm verwendet. Dieser Konverter setzt auf den Normal Mapper Source Code, den Sie auch bei ATI downloaden können, auf. Auch können Sie damit gleich Tangent Spaces berechnen und speichern.

Rendern mit Object Space Normal Maps

Mit unserem Direct3D Framework können Sie die so konvertierten obj-Dateien laden. Es wurde der Vollständig­keit halber modifiziert, weil das ursprüngliche OBJ-Format keine Tangent Spaces vorsieht. Statt dem Token vn für Normale wurde das vx Token gefolgt von drei Vektoren (Normale, Binormale, Tangente) eingeführt.

Bei der hier vorgestellten Object-Space-Bump Mapping-Technik benötigen Sie pro Vertex aber nur die Textur-Koordinaten. Die Vertex und Pixel Shader definieren Sie zum Beispiel wieder in einer Direct3D-Effect-Datei, die wir Ihnen an dieser Stelle für Pixel Shader 2.0 Karten zeigen.

Der benötigte Vertex Shader ist denkbar einfach. Sie transformieren einfach die Vertices entsprechend der World-View-Projection-Matrix, reichen die Textur-Koordinaten für die Normal Map durch und übergeben die World Space Koordinate (in diesem Fall entspricht das auch der Object Space Koordinate) in der zweiten Textur Koordinate an die Rasterisierungs­stufe:

struct FRAGMENT {
	float4 position : POSITION;
	...//siehe Heft-CD
};

FRAGMENT vsBump(VERTEX vertex)
{
	FRAGMENT result;
	....
	return result;
}
		

Während der Rasterisierung berechnen Sie dann das Modell per Pixel, nachdem Sie die dazu benötigte Normale aus der Normal Map ausgelesen und auf das entsprechende Intervall skaliert haben:

FRAGRESULT psBump(FRAGMENT fragment)
{
	FRAGRESULT result; //siehe Heft-CD
	....
	return result;
}
		

Rendern mit Tangent Space Normal Maps

Auch wenn Sie Tangent Space Normal Maps verwenden, bringt das Vorteile: Durch die Auflösung der generierten Normal Map ist auch der Detailgrad der Oberfläche eines Objektes begrenzt und die Auflösung der Textur lässt sich natürlich nicht beliebig steigern. Wie beim herkömmlichen Texturieren können Sie Detail Maps einsetzen, d.h. Texturen oder in diesem Fall Bump Maps, die nur sichtbar sind, wenn sich der Betrachter nahe am Objekt befindet, die zudem feine Strukturen aufweisen.

Aber genau für diese Detail Maps, die mehrfach aneinander­gelegt auf die Oberfläche gemapped sind, benötigen Sie Tangent Space Bump Mapping, da Sie sonst die Textur-Koordinaten nicht frei wählen können. Glücklicher­weise können Sie mit dem Normal Mapper Tools auch diese Art der Normal Maps erzeugen und mit dem Konverter gleich die entsprechenden Tangent Spaces im obj-Format speichern. Somit ändern Sie nur noch das Effect File. Zunächst benötigen Sie mehr Attribute pro Vertex, eben den Tangent Space:

struct VERTEX {
	float4 position : POSITION;
	float3 normal : NORMAL;
	float3 tangent : TEXCOORD0;
	float3 binormal : TEXCOORD1;
	float4 texcoord : TEXCOORD2;
};
		

Im Vertex Shader berechnen Sie dann den Vektor von jedem Vertex zur Lichtquelle und transformieren ihn mit drei Skalar­produkten in den Tangent Space:

struct FRAGMENT
{
	float4 position: POSITION;
	float3 texture0: TEXCOORD0;
	float3 osPos : TEXCOORD1;
	float3 tsLight : TEXCOORD2;
};

FRAGMENT vsBump(VERTEX vertex)
{
	FRAGMENT result;
	result.position = mul(matWVP, vertex.position);
	float4 lightDir =
		normalize(lightPosition - vertex.position);

	result.tsLight.x =
		dot(lightDir, vertex.tangent);
	result.tsLight.y =
		dot(lightDir, vertex.binormal);
	result.tsLight.z =
		dot(lightDir, vertex.normal);
	result.tsLight.w = 1.0;

	result.tsLight = normalize(result.tsLight);
	result.osPos = vertex.position;
	result.texture0 = vertex.texcoord;

	return result;
}
		

Im Pixel Shader lesen Sie wie bisher die Normale aus, die dann bereits im Tangent Space vorliegt. Da die Komponenten des Vektors zur Lichtquelle während der Rasterisierung linear interpoliert werden, müssen Sie diesen für jeden Pixel normalisieren:

FRAGRESULT psBump(FRAGMENT fragment)
{
	FRAGRESULT result;
	float4 normal, lightDir; // normale auslesen
	normal = tex2D(normalSampler, ..
	// beispiel: diffuse beleuchtung
	result.color= dot(lightDir, normal);
	return result;
}
		

Ausblick

Ein UV-Mapping, wie Sie es für die Normal Maps benötigen, erlaubt es, nahezu beliebig kontinuier­liche Werte für Punkte auf der Objekt­oberfläche zu speichern. Dadurch ergeben sich weitere Einsatzgebiete. Mit dem ATI Normal Mapper können Sie zusätzlich zu den Normalen eine so genannte Bent Normal berechnen. Um die Bent Normal zu bestimmen, verfolgen Sie zunächst einen Strahl von der Oberfläche der Low-Polygon-Objektes und berechnen den Schnittpunkt mit dem hoch aufgelösten Dreiecksnetz. Anschließend tasten Sie von diesem Schnittpunkt aus die Halbkugel über der Oberfläche durch eine größere Anzahl von Strahlen ab. Strahlen, die keine Flächen des Objektes schneiden, werden gemittelt und das Resultat ist die Bent Normal. Dieser Vektor zeigt in die Richtung, aus der am meisten Licht auf die Objekt­oberfläche einfällt. Sie verwenden dies, um diffuses Environment Mapping zu simulieren.

Ähnliches berechnet der Normal Mapper auch beim Occlusion Term Modus. Wiederum tasten Sie die Hemisphäre über dem Schnittpunkt mit dem High-Polygon-Modell ab, wozu übrigens 261 oder 581 Strahlen verschossen werden, und Sie speichern den Prozentsatz der Strahlen ohne weitere Schnittpunkte. Dieser Term dient dann dazu, die ambiente Beleuchtung abzudunkeln, um eine Art Selbst­beschattung zu simulieren.

Eine ganz andere Art der Anwendung solcher UV-Mappings vermag, Subsurface Scattering Effekte darzustellen. Da grundlegende Idee ist dabei folgende: Sie zeichnen das 3D-Objekt in eine Textur. Allerdings verwenden Sie die Textur-Koordinaten als 2D-Koordinaten für das Rendering und transformieren nicht etwa die Modell-Koordinaten. Bei diesem Rendering Pass berechnen Sie neben der Beleuchtung, wie viel Licht an der entsprechenden Stelle des Objekts in das Material eindringt. Anschließend setzen Sie eine vorberechnete Tabelle ein, um für jeden Vertex des Dreiecksnetzes zu bestimmen, wie viel Licht von den anderen Oberflächen­teilen bis zu ihm durch das Material dringt. Hier reicht eine Rechnung pro Vertex, da die Intensitäts­verläufe meist niederfrequent sind. Auch dieser Schritt lässt sich mit Multipass Rendering und Dependent Textur Lookups in Hardware durchführen. Im abschließenden Render Pass verwenden Sie die Vertex-Intensitäten, die auch in einer Textur gespeichert wurden. Genaueres zu diesem Verfahren finden Sie in dem Paper: GPU Algorithms for Radiosity and Subsurface Scattering (http://graphics.cs.uiuc.edu/~nacarr/papers/gpuradsub.pdf).