Raum ohne Rechenaufwand

Carsten Dachsbacher

In mehreren bisherigen Ausgaben von PC Underground haben Sie verschiedene Methoden kennen gelernt, die alle unter den Begriff Bump Mapping fallen. Allen diesen Verfahren, wie Emboss, Dot-Product 3 oder Bump Mapping mit per Pixel Lighting (ab Pixel Shader 2.0) ist gemein, dass sie die Oberfläche selbst nicht verändern – lediglich die Oberflächen­normale wird bei der Beleuchtungs­berechnung modifiziert, um den Eindruck von komplexen Oberflächen­strukturen zu erwecken. Oft genannt ist auch der Begriff Displacement Mapping. Dies ist die naheliegenste und aufwändigste Variante, um komplexe Oberflächen darzustellen: Die Oberfläche wird in eine Vielzahl von kleinen Dreiecken unterteilt. Die dadurch entstehenden Eckpunkte werden senkrecht zur Oberflächen­normale, entsprechend einer Höhenfunktion oder Textur, verschoben. Für die neuen Vertices werden auch neue Normalen berechnet, um die Beleuchtung anzupassen.

Das hier vorgestellte Parallax Bump Mapping reiht sich in die oben genannten Verfahren ein, d.h. nur in die Beleuchtungs­berechnung wird eingegriffen. Aber es hat ein zusätzliches Feature, das den räumlichen Eindruck weiter verstärkt. Zuvor begleiten wir Sie aber bei einem kleinen mathematischen Exkurs, um die Grundlagen für perfektes Bump Mapping zu schaffen.

Tangent Space

Der Tangent Space ist das wichtigste Konzept beim Bump Mapping mit Normal Maps – auch als Bump Maps bezeichnet. Normal Maps sind nichts anderes als Texturen, deren Farbwerte Oberflächen­normalen kodieren und zwar so, dass die rot/grün/blau-Werte die X/Y/Z-Komponenten der Normale sind. Diese Normal Maps werden wie normale Texturen auf eine Oberfläche abgebildet. Bei der Beleuchtungs­berechnung, die Sie für jeden Pixel durchführen, wird die Normale ausgelesen. Allerdings können Sie diese Normale nicht direkt verwenden, weil in den Normal Maps die Orientierung der gerade zu zeichnenden Oberfläche nicht enthalten ist. Normal Maps konstruieren Sie, als würde die Textur auf der X/Y-Ebene liegen und die Z-Komponente nach oben zeigen.

An dieser Stelle kommt nun der Tangent Space in Spiel. Dieser ist ein Koordinaten-System aus drei Achsen, das für jeden Vertex definiert ist: Die X- und Y-Achse liegen in der Tangential­ebene an der Oberfläche an dem Vertex. Diese beiden Achsen werden klassischer­weise mit Tangente und Binormale bezeichnet, obwohl für letztere die Bezeichnung Bitangente korrekt wäre. Die Z-Achse ist gleich der Vertex-Normalen.

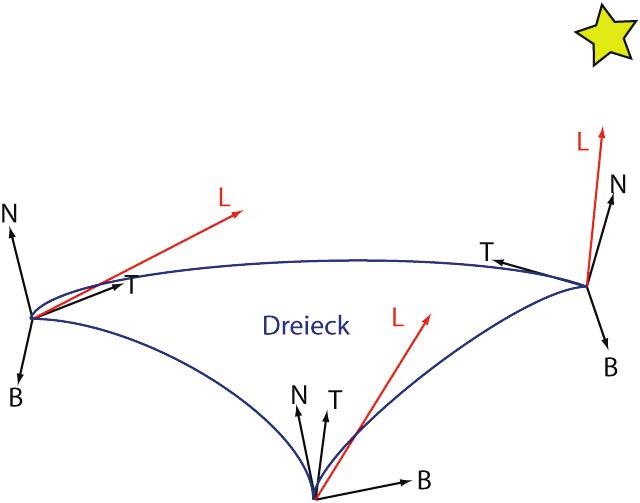
Diese Definition des Tangent Space ist konform mit der der Normal Maps: Wenn Sie die Richtung zur Lichtquelle L und zum Betrachter V, die Sie für die Beleuchtungs­berechnung benötigen, in den Tangent Space transformieren, können Sie die Normale aus der Normal Maps auslesen und direkt für die Beleuchtungs­berechnung verwenden. Das Beispiel zeigt dies mit Halfway-Vektoren und HLSL-Syntax:

float3 H = normalize(L + V);
float3 N = tex2D(bumpMap,texCoord) * 2 ? 1;
I = saturate(dot(N,L)) * diffuseColor +
	pow(saturate(dot(H, N)), spec) * specColor;
		

Die Skalierung und Verschiebung des Wertebereichs bei der Normale ist notwendig, da in der Textur Werte aus [0;1] enthalten sind. Die Komponenten der Normalen werden zum Speichern in der Textur vom Intervall [-1;1] in das Intervall [0;1] abgebildet, um sie als RGB-Farbwerte repräsentieren zu können. Solche Normal Maps können Sie mit diversen Tools wie von nVidia (siehe Literatur) aus Graustufen-Höhenbildern erzeugen. Die Tangent Spaces berechnen Sie also pro Vertex, d.h. Sie ändern sich auch über ein zu zeichnendes Dreieck. Das stellt aber kein Problem dar: Sie berechnen die Trans­formationen in den Tangent Space in einem Vertex Shader und die Grafikkarte interpoliert die entsprechenden Vektoren für Sie.

Berechnung des Tangent Space

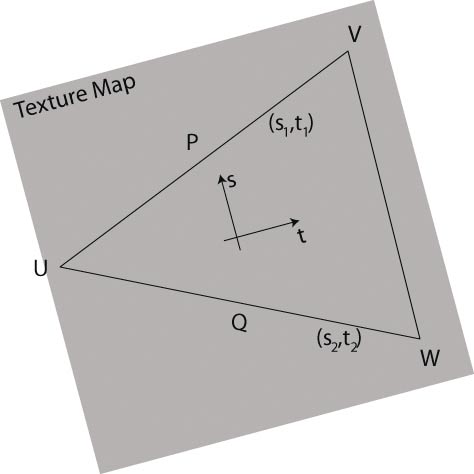
Damit diese Interpolation gut geht, müssen Sie darauf achten, dass die Tangent Spaces der drei Eckpunkte eines Dreiecks sinnvoll gewählt sind. Die einfachste Variante liefert in vielen Fällen akzeptable Ergebnisse. Sie ist einfach abhängig von der Normalen, einen Tangent Space zu konstruieren. Nehmen Sie an, die Normale des Vertex ist N=(nx,ny,nz). Ein Vektor, der sicher nicht dieselbe Richtung hat (es sei denn, N wäre Nullvektor), ist A=(ny, -nz, nx). Durch ein Kreuzprodukt erhalten Sie einen der Tangential­vektoren T=N x A und durch ein weiteres, den zweiten: B=T x N. Das ist alles leicht in einem Vertex Shader zu berechnen, aber bessere Ergebnisse erhalten Sie, wenn Sie den Tangent Space an dem Mapping der Texturen ausrichten.

Betrachten Sie dazu das Bild rechts unten: Eine Textur wird auf ein Dreieck (UVW) abgebildet, wobei P=(px,py,pz)T und Q=(qx,qy,qz)T die Differenz­vektoren der Eckpunkte (V-U) bzw. (W-U) sind. Die Differenz­vektoren der Textur-Koordinaten sind (s₁,t₁)T bzw. (s₂,t₂)T, d.h. der Wert s1 kennzeichnet die erste Komponente der Textur-Koordinate von V minus der Ersten von U usw. Nun wollen wir zunächst den Tangent Space für dieses Dreieck bestimmen. Die Normale des Tangent Space, also die Z-Achse, ist gleich der Normalen des Dreiecks. Es verbleiben also die beiden Tangenten, die entlang der Ableitung der Textur-Koordinaten zeigen sollen. Anschaulich bedeutet das: Wenn Sie den Vektor (s₁,t₁)T, gegeben im Tangent Space, aus diesem heraus transformieren, wollen Sie den Vektor P erhalten. Diese Transformation heißt, die beiden Komponenten mit der Tangenten bzw. Binormalen zu multiplizieren und zu addieren: P = s₁T+t₁B bzw. P = s₂T+t₂B

Was also bleibt, ist ein Gleichungs­system mit sechs Unbekannten, nämlich den Komponenten von T und B, das sich mit Matrizen wie folgt beschreiben lässt:

|px py pz|   |s1 t1|   |Tx Ty Tz|
|        | = |     | * |        |
|qx qy qz|   |s2 t2|   |Bx By Bz|
		

Dieses lösen Sie, indem Sie die Matrix mit den Differenzen der Textur-Koordinaten invertieren und danach an beiden Seiten multiplizieren:

|s1 t1|-1          1        |t2 -t1|
|     |     = ––––––––––– * |      |
|s2 t2|       s1*t2-s2*t1   |-s2 s1|
		

Auf der rechten Seite bleiben lediglich die Unbekannten. Nachdem Sie die Gleichungs­seiten getauscht haben, erhalten Sie:

|Tx Ty Tz|
|        | =
|Bx By Bz|

      1       |t2 -t1|   |px py pz|
––––––––––– * |      | * |        |
s1*t2-s2*t1   |-s2 s1|   |qx qy qz|
		

So erhalten Sie also T und B für ein Dreieck, benötigen aber je einen Tangent Space pro Vertex.

Dafür legen Sie ein Array an, das für jeden Vertex drei Vektoren speichert. Diese initialisieren Sie zunächst mit Null. Anschließend berechnen Sie für jedes Dreieck den Tangent Space und addieren N, T und B auf den Tangent Space seiner Eckpunkte.

Abschließend müssen Sie die Tangent Spaces pro Vertex (bezeichnet mit NV, TV, BV)) noch orthogonali­sieren – wie im Folgenden mit der Gram-Schmidt-Orthogonali­sierung. Um für jeden Vertex später nicht drei Vektoren zu speichern, merken Sie sich lediglich die eine der Tangenten und die Orientierung des Tangent Spaces, also ob es sich um ein links- oder rechtshändiges Koordinaten­system handelt. Die zu speichernde Tangente – ein vier-Komponenten Vektor also – ist dann:

T.xyz = TV ? (NV dot TV)NV
T.w = (NV x TV) dot BV < 0 ? -1 : 1
		

In einem Vertex Shader können Sie die Binormale aus dem obigen Vektor und der Normalen leicht berechnen (HLSL Syntax):

float3 B = cross(N, T.xyz) *T.w;
		

Bump Mapping mit Per-Pixel-Lighting

Mit den obigen Berechnungen, deren Implementation Sie wie immer in unserem Beispiel­programm vorfinden, haben Sie alles in der Hand, um Bump Mapping mit Per-Pixel-Lighting (Pixel Shader 2.0) durchzuführen.

Für die Operationen im Vertex Shader haben Sie zwei Optionen: Entweder Sie führen die Berechnungen im Object Space durch, oder Sie nehmen alle Berechnungen im World Space vor. Wir beschreiben hier die letztere Variante, die zum einen weniger und zudem weniger schwierige Operationen benötigt, wenn Sie mehrere Lichtquellen in der Szene verwenden. Im Vertex Shader berechnen Sie – außer der gewöhnlichen Koordinaten­transformation – die Binormale und transformieren N, T und B anhand der Transformation Ihres Objektes (Matrix matWV). Außerdem benötigen Sie die World Space Position des Vertex:

N = mul(matWV, vertex.Nv);
T = mul(matWV, vertex.Tv.xyz);
B = cross(normal,tangent) * vertex.Tv.w;

// world space vertex pos
wsPos = mul(matWV, vertex.position);

// view/light vector
V = normalize(cameraPosition - wsPos);
L = normalize(lightPosition - wsPos);
		

Anschließend transformieren Sie V und L in den Tangent Space (Vt, Lt), indem Sie die Skalarprodukte von V beziehung­sweise L mit T, B und N bilden. Ihr besonderes Augenmerk gilt dabei der Reihenfolge der Verktoren in diesem Skalarprodukt:

Lt = float3(dot(T,L), dot(B,L), dot(N,L));
		

Die Reihenfolge TBN ist wichtig: Erinnern Sie sich an die Normal Maps – die Z-Komponente zeigt von der Fläche weg, entspricht also der Normalen!

Die Grafikkarte interpoliert nun für Sie V und L (im Tangent Space) und Ihnen stehen die Werte im Pixel Shader zur Verfügung. Dort normalisieren Sie sie, lesen die Normal Map und gegebenenfalls weitere Texturen mit diffusen und spekularen Farbwerten und berechnen die Beleuchtung wie oben. Das Resultat sehen Sie im Bild links.

Parallax Bump Mapping

Als Parallaxe bezeichnet man ganz allgemein die scheinbare Positions­änderung eines Objektes durch eine Verschiebung der Position des Beobachters. Wenn Sie nun eine unebene Oberfläche – repräsentiert durch eine Normal Map – auf ein planares Dreieck abbilden, geht die dafür notwendige Höhen­information verloren und die Oberfläche wirkt flach. Das folgende Bild zeigt, was in diesem Fall passiert: Die Textur oder Normal Map wird an der Stelle A ausgelesen, obwohl Sie die tatsächliche Oberfläche an Punkt B sehen würden. Wenn Sie also die Textur-Koordinate für jeden zu zeichnenden Pixel korrigieren können, würden Sie einen Parallax-Effekt simulieren. Dazu benötigen Sie außer der Normalen aus der Normal Map noch eine Höhen­information. Hohe Bereiche verursachen eine Verschiebung der Textur-Koordinate in Richtung des Betrachters, niedrige Bereiche eine Verschiebung in die andere Richtung. Die Höhen­information können Sie entweder durch separate Textur zugänglich machen oder im Alpha Kanal der Normal Map speichern.

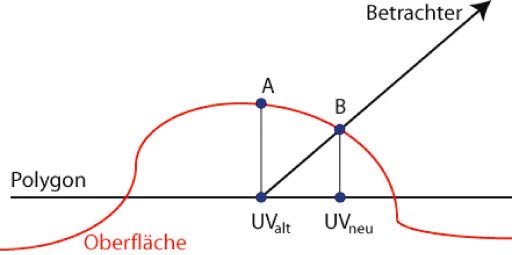
Was Sie also für den Parallax-Effekt benötigen sind drei Dinge: eine ursprüngliche Textur-Koordinate, die durch die Texturierung gegeben ist, die Richtung zum Betrachter im Tangent Space (Vt) und den eben genannten Höhenwert der Oberfläche gespeichert in einer Textur. Den Höhenwert, der in der Textur den Wertebereich [0;1] einnimmt, skalieren und verschieben Sie auf [-x;x], wobei x ein sehr kleiner Wert ist, etwa von der Größenordnung 0.02. Die verschobene Textur-Koordinate UVneu berechnen Sie aus der alten UValt:

UVneu = UValt + height * Vt.xy / Vt.z
		

Diese Berechnung stimmt allerdings nur unter einer Voraussetzung. Nämlich dann, wenn die Höhe bei A gleich der bei B ist, was in den seltensten Fällen so sein wird. Wenn Sie nahezu senkrecht auf eine Oberfläche sehen, werden die Textur-Koordinaten-Differenzen kleiner und die obige Annahme ist akzeptabel. Wenn Sie flacher auf eine Oberfläche blicken, werden die Verschiebungen der Textur-Koordinaten aber unendlich groß. Also gilt es, die Offsets nach oben zu beschränken. Die einfachste und funktionier­ende Variante ist, die Verschiebung auf den Höhenwert bei A zu beschränken. Diese Option reduziert gleichzeitig den Berechnungs­aufwand, denn Sie erreichen genau das mit folgendem Code:

UVneu = UValt + height * Vt.xy
		

Die Verschiebung kann nicht größer als height sein, da der Vektor Vt normalisiert ist und auch seine 2D-Projektion Vt.xy maximal die Länge 1 haben kann. Um Parallax Bump Mapping zu erhalten, müssen Sie lediglich Ihren normalen Bump Mapping Pixel Shader so erweitern, dass an der interpolierten Textur-Koordinate zunächst der Höhenwert ausgelesen wird.

V = normalize(fragment.V);
height = tex2D(heightMap, fragment.UValt);
height = height * 0.04 - 0.02;
UVneu = fragment.UValt + height * V;
		

Die Normale und weitere Oberflächen­attribute lesen Sie an der Stelle UVneu aus Texturen aus. Die Verschiebung der Textur-Koordinaten ist nur eine Approximation der Oberflächen­beschaffenheit. Deswegen müssen Sie bei der Gestaltung von Height Maps und deren Skalierung etwas probieren, bis Sie ein optimales Ergebnis erhalten. Die besten Resultate erzielen Sie, wenn Sie Height Maps ohne Sprünge und nicht zu starken Variationen anlegen. Bei Oberflächen mit sehr steilen Flanken würden sich außerdem Teile gegenseitig verdecken – ein Effekt, den Sie mit Parallax Bump Mapping ohnehin nicht erzielen können.