Punktspiele

Carsten Dachsbacher/Nils Pipenbrinck

Nach den Ausflügen der letzten beiden Ausgaben in die Welt der 3D-Grafik kehren wir in die zweite Dimension zurück. Um Begriffe wie Perspektive oder Projektion brauchen Sie sich also nicht mehr zu kümmern. Vielmehr arbeiten Sie mit einfachen Bitmaps und anderen zwei­dimensionalen Tabellen.

Die Spielereien mit einzelnen Bildpunkten sind dabei nicht nur einfach, sondern auch schön: Mit geringem Aufwand programmieren Sie auf diese Weise atemberaubend schöne Sinnes­eindrücke.

Einfaches Motion Blur

Harte Übergänge in Bildfolgen schwächen Sie durch das sogenannte Motion Blur ab. Dieser Effekt der Bewegungs­unschärfe ist sehr einfach zu erreichen: Sie mischen das aktuelle Bild eines Effekts mit dem vorhergehenden, indem Sie für jedes Pixel die Mischfarbe aus altem und neuem Pixel berechnen. So erkennen Sie die letzten vier bis fünf Bilder unter dem aktuellen. Die Bewegung sieht weicher aus, da starke Übergänge zwischen den Bildern verwischen.

Einfach, aber effektiv. Das gemischte Bild wird gleich wieder in den Puffer für das vorherige Bild geschrieben und ist einfach darstellbar.

Die Mischfarbe zweier Pixel berechnen Sie, indem Sie jeweils die rote, grüne und blaue Komponente addieren und halbieren. Als Ergebnis erhalten Sie die Farb­komponenten der neuen Farbe. Dieses Verfahren ist zwar das naheliegendste, aber auch recht aufwendig.

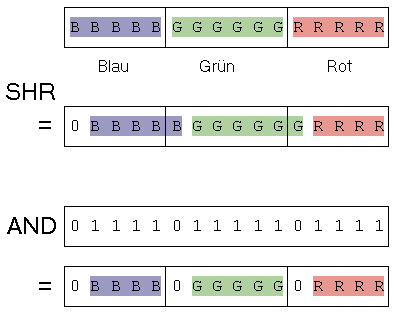
Mit einem kleinen Trick behandeln Sie nicht nur alle drei Farb­komponenten, sondern auch gleich zwei Pixel in einem Ablauf. Zunächst einmal betrachten Sie ein Pixel im Highcolor-Format: Es besteht aus jeweils 5 Bits für die Rot- und Blau-Komponente, 6 Bits sind für den Grün-Anteil reserviert.

Schieben Sie die Bits um eine Stelle nach rechts. Dies entspricht einer Division durch 2. Nun maskieren Sie mit 0111101111101111 die Bits aus, die durch das Schieben in die falsche Farbkomponente gerutscht sind Wenn Sie zwei derart vorbereitete Pixel addieren, erhalten Sie wieder ein Pixel im Highcolor-Format. Da Sie die Division der Addition vorziehen, verlieren Sie pro Farbkomponente ein Bit Genauigkeit. Dies entspricht einem Fehler von etwa 1,5 Prozent. Sie werden den Unterschied jedoch kaum wahrnehmen. Addieren Sie die Farb­komponenten hingegen vor der Division, verfälscht der nun entstandene Überlauf den benachbarten Farbwert.

Sie sollten immer zwei Pixel gleichzeitig mischen, da 32-Bit-Operationen im 32-Bit-Protected-Mode viel schneller sind. Dieser Code zeigt, wie es geht:

//Zeiger auf das aktuelle Bild
unsigned long *data1;
//Zeiger auf das vorherige Bild
unsigned long *data2;

for(int i = 0;i < AnzahlPixel / 2; i++)
{
	unsigned long a = (data1[i] >> 1) & bitmask;
	unsigned long b =
		(data2[i] >> 1) & bitmask;
		data2[i] = ( a + b);
}
		

Die Listings zu diesem Beitrag enthalten auch eine Assembler-Implemen­tierung dieses Algorithmus. Durch ihre Einfachheit ist diese Implemen­tierung ein hervorragendes Beispiel, um sich mit Assembler-Programmierung vertraut zu machen.

Viele Programmierer benutzen diese Technik, um Fehler in ihren Routinen zu kaschieren. Zum Beispiel treten bei vielen 3D-Engines – nicht so bei der von PC Underground verwendeten – an den Polygonkanten schwarze Punkte auf. Durch den Motion-Blur-Effekt verschwinden sie zwar nicht vollständig, fallen aber immerhin nicht mehr so stark auf.

Zwei Bilder überblenden

Weiche Überblendungen von Bildern eignen sich gut, um nahtlos von einem Effekt in einen anderen zu wechseln. Da das Misch­verhältnis der zwei Bilder frei einstellbar sein soll, funktioniert dies nicht mehr so einfach wie beim Motion Blur. Die Bilder sollten bei diesem Effekt in Truecolor (ein Byte pro Farbkomponente) vorliegen. Mit MMX-Befehlen schreiben Sie zwar auch sehr schnelle Mischroutinen für Highcolor, aber die meisten C-Compiler unterstützen leider keine MMX-Befehle.

Mischen Sie zwei Farben mit einfacher linearer Interpolation. Den Mischgrad geben Sie in Byte an:

Mischwert= A + ((B - A) * Mischgrad) / 255
		

Multi­plikationen und Divisionen sind auf x86-Prozessoren bekanntermaßen sehr langsam. Mischen Sie jedoch Bytes, können Sie alle Ergebnisse der Interpolation in einer kleinen Tabelle vorberechnen.

Der Ausdruck (B-A) kann Werte zwischen -255 und 255 annehmen. Der Mischgrad selbst ist bei jedem Aufruf der Routine konstant. Sie berechnen also alle 512 möglichen Werte vor:

signed int Mischtabelle[512];

for(int i = 0; i < 512; i++)
	Mischtabelle[i] = ((i - 255) * Mischgrad) / 255;
		

Anschließend mischen Sie die zwei Bilder und ersetzen die Interpolation durch einen Tabellen­zugriff. Gleichzeitig konvertieren Sie das Ergebnis in das Highcolor-Format, um das Mischbild darstellen zu können. Da (B-A) auch negative Werte annehmen kann, gleichen Sie dies durch eine Addition mit 255 aus.

//Ausgangsbilder, Truecolor 24 Bit
unsigned char *bild1,bild2;

//Zielbild, Highcolor
unsigned short *mischbild;

for(int i = 0;i < AnzahlPixels; i++)
{
	signed long a,b;
	unsigned short Pixel;

	//Rot-Anteile mischen
	a=bild1[i * 3 + 0];
	b=bild2[i * 3 + 0] - a + 255;
	Pixel=Rtab[a+Mischtabelle[b]];

	//Grün-Anteile mischen
	a=bild1[i *3 + 1];
	b=bild2[i *3 + 1] - a + 255;
	Pixel |= Gtab[a + Mischtabelle[b]];

	//Blau-Anteile mischen
	a=bild1[i * 3 + 2];
	b=bild2[i * 3 + 2] - a + 255;
	Pixel |= Btab[a+Mischtabelle[b]];

	mischbild[i]=Pixel;
}
		

Fraktale Plasmawolken

Plasmawolken kommen in Demoeffekten häufig zum Einsatz. Sie eignen sich hervorragend für einfache Texturen und für Effekte aller Art. Aber auch als kontrollierter Zufalls­zahlen­generator leisten Sie gute Dienste.

Es gibt zahlreiche Algorithmen, um fraktale Plasmawolken zu erzeugen. Für die folgenden Effekte benötigen Sie jedoch einen ganz speziellen Typ. Die Plasmen müssen „seamless“, also nahtlos sein. Das heißt, Sie können die Bilder wie Kacheln auf dem Bildschirm auslegen und bekommen keine sichtbaren Nahtstellen zwischen den Einzelteilen.

Diese Plasmen erzeugt in der Regel ein rekursiver Algorithmus, der jedes Quadrat in vier kleinere Quadrate aufteilt. Die neu erzeugten Punkte berechnen Sie, indem Sie die vier umgebenden Punkte mitteln sowie einen Zufallswert addieren.

Da die Plasmen in unserem Fall eine feste Breite und Höhe von 256 Pixeln haben, können Sie die Rekursion einfach durch eine Schleife ersetzen. Dies macht den Code in der Datei plasma.cpp über­sichtlicher und schneller. Beim Erzeugen der Plasmen können Sie zusätzlich den Startwert des Zufallszahlen-Generators sowie den Grad des Zufalls angeben.

Animierte Verzerrungen mit Plasmen

Plasmawolken besitzen eine sehr nützliche Eigenschaft: Nahe beieinander liegende Pixel haben ähnliche Werte, aber über das Plasma selbst sind die Werte sehr zufällig verteilt. Diese Eigenschaft können Sie für einen Demoeffekt nutzen, den Sie als Vollbildeffekt sowie als sehr schönen Texture-Generator einsetzen können.

Zunächst generieren Sie zwei Plasmabilder. Das erste soll Ihr Ausgangsbild sein, das zweite dient dazu, eben dieses Ausgangsbild zu verzerren. Nun legen Sie zwei Tabellen xoffset und yoffset an, die für einen eingegebenen Wert einen Verschiebungs­wert liefern. Zeichnen Sie das Bild Pixel für Pixel, und lesen Sie den Farbwert des entsprechenden Pixels aus dem zweiten Plasmabild. Diesen Wert nehmen Sie als Eingabewert der Tabellen und erhalten somit eine Verschiebung für die x- und y-Richtung. Diese Verschiebung gibt an, welches Pixel Sie aus dem ersten Plasmabild an das aktuelle Pixel kopieren.

Sie kopieren also nicht 1:1, sondern verzerren die Punkte des Quellbildes leicht anhand des zweiten Plasmas. Die Tabellen xoffset und yoffset füllen Sie dabei mit Werten ganz nach Ihrem Geschmack. Auf der Sinusfunktion basierende Kreisbahnen haben sich dabei bewährt. Sie sehen immer sehr gut aus.

Probieren Sie ruhig einmal an den Parametern herum. Sie können damit zum Beispiel marmorierte Texturen erzeugen. Und wenn Sie bei jedem Bildaufbau die Parameter leicht ändern, bekommen Sie eine tolle Bewegung ins Bild. Dieser Effekt eignet sich hervorragend als Hintergrund für ein Logo.

Der Algorithmus erzeugt wieder 256 x 256 Pixel große Texturen. Das Beispiel­programm kachelt das Fenster mit der Textur aus, um einen schwarzen Rand zu vermeiden.

for(int y = 0;y < < 256; y++)
{
	for(int x = 0; x < 256; x++)
	{
		//Plasma-Wert lesen
		unsigned char plasmawert = plasma[256 * y + x];

		//Berechnen der Verschiebung aus den Tabellen
		unsigned char xx = x + xoffset[plasmawert];
		unsigned char yy = y + yoffset[plasmawert];

		//Kopieren des verschobenen Pixels
		ziel[256 * y + x] = quell[yy * 256 + xx];
	}
}
		

Auf diesem Algorithmus bauen Sie leicht zahlreiche neue Effekte auf. Versuchen Sie zum Beispiel, ein Bild mit Logo als Verzerrquelle zu benutzen, oder nehmen Sie als Quelltextur ein gestreiftes Bild. So entstehen holzähnliche Texturen.

Die C-Variante des Algorithmus ist recht langsam. Zum Vorberechnen von Texturen ist sie aber allemal geeignet. Im Code finden Sie deshalb eine schnelle Assembler-Version.

Sinusplasmen

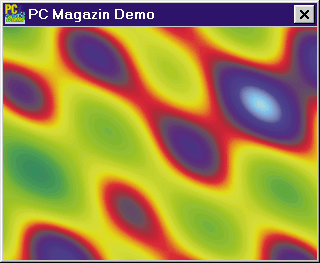
Da Sie sich gerade mit Plasmen beschäftigen, wollen wir Ihnen einen Klassiker der Demo-Programmierung nicht vorenthalten: Sinusplasmen. Diese haben schon immer einen großen optischen Reiz ausgeübt.

Sinusplasmen entstehen, wenn Sie mehrere überlagerte Sinus­funktionen berechnen und als Bitmaps darstellen. Die Vorgehensweise ähnelt dabei stark dem Texture Mapping. Da eine Sinus-Welle jedoch eindimensional ist, fällt der Code wesentlich kompakter aus. Auch füllen Sie den ganzen Bildschirm, so daß die aufwendige Berechnung der Polygonkanten nicht nötig ist.

Der Programmcode weiter unten berechnet für jedes Pixel das Argument der Sinusfunktion. Da Sie nur am optischen Ergebnis des Effekts interessiert sind, wäre es Zeit­verschwendung, diese Funktion für jedes Pixel aufzurufen. Sie sollten sich daher eine Tabelle anlegen.

Ein Vorteil der Tabelle ist, daß Sie nicht mehr auf die Sinus­funktionen festgelegt sind. Probieren Sie einmal andere Tabellen­einträge aus. Die Bewegung in diesem Effekt entsteht, indem Sie die Startwerte der Plasma­berechnung von Bild zu Bild variieren.

//Zeiger auf Highcolor-Zielbild
short *picture;
//Zeiger auf Highcolor-Palette
short *palette;
//Zeiger auf Sinus-Tabelle
int *sinetable;

//Geschwindigkeit der Wellen vorberechnen
int speed_x=3000*sin(time);
int speed_y=3000*cos(time);

//Startwert der Welle setzen
int wave_y=0;

//Schleife über die Höhe des Bitmaps
for(int y = 0; y < height; y++)
{
	//Aktuellen Wellen-Wert sichern
	int wave_x = wave_y;

	//eine Scanline zeichnen
	for(int x=0; x < width; x++)
	{
		//Punkt setzen
		*(picture++) = palette[sintable[wave_x % Tabellen_Groesse]];
		//Geschwindigkeit in X-Richtung addieren
		wave_x += speed_x;
	}
	//Geschwindigkeit in X-Richtung addieren
	wave_y += speed_y;
}
		

Diese Programmzeilen berechnen nur eine einzelne Welle. Für ein wirklich hübsches Sinusplasma brauchen Sie mehrere davon. Die entsprechende Erweiterung ist sehr einfach, macht den Code aber unüber­sichtlich. Den vollen Quelltext sehen Sie in der Datei sinplas.cpp bzw. sinplas.h.

2D-Bumpmapping

Im ersten PC-Underground-Artikel (Ausgabe 7/98, ab S. 228) haben Sie bereits eine Lichtquelle über ein Bild bewegt. An dieser Stelle werden Sie diesem Bild noch eine drei­dimensionale Struktur hinzufügen, die sich dann in der Schattierung durch die Lichtquelle bemerkbar macht. Bei dieser Art der Schattierung spricht man von Bumpmapping (der englische Begriff Bump bedeutet Beule). Daß diese Übersetzung treffend ist, sehen Sie am Beispiel­programm.

Die drei­dimensionale Struktur erhalten Sie, indem Sie jedem Pixel des Bildes eine Höhe zuweisen und so höhere und tiefere Bereiche (Beulen) für das Bild erhalten. Die Höhe eines Pixels bestimmen Sie zum Beispiel anhand von mathematischen Funktionen. Einfacher berechnen Sie die Höhe anhand der Helligkeit eines Pixels, was meistens auch in einem sehr interessanten Effekt resultiert. Die Helligkeit entspricht der Summe der Rot-, Grün- und Blau-Anteile eines Pixels.

Wenn Sie die Bitmap-Laderoutinen der Grafik­bibliothek verwenden, berechnen Sie die Helligkeit wie folgt:

for(j = 0; j < SCREEN_Y; j++)
	for(i = 0;i < SCREEN_X; i++)
	{
		pixel = bild[i+j * SCREEN_X];
		helligkeit=
			(bmpheader.cColors[pixel * 4]+
				bmpheader.cColors[pixel *4 + 1]+
				bmpheader.cColors[pixel *4 + 2]);
		heightmap[i + j * SCREEN_X] = helligkeit;
	}
		

Nachdem Sie die Höhe eines jeden Pixels berechnet haben, ermitteln Sie für jedes Pixel die „Neigung“ des Bildes an dieser Stelle. Dazu bilden Sie an einem Punkt (X/Y) für die horizontale Neigung die Differenz aus der Höhe des Punkts links und des Punkts rechts davon. Analog erhalten Sie die vertikale Neigung durch die Differenz des darüber- und des darunter­liegenden Punkts.

Diese beiden Werte verwenden Sie später bei der Berechnung des Bildes. Deshalb speichern Sie sie in der sogenannten Bumpmap. Eine Bumpmap verfügt immer über doppelt so viele Einträge, wie die Auflösung des Bildes beträgt. Jeweils zwei aufeinander­folgende Werte enthalten die zusammen­gehörigen Neigungen eines Pixels. Die Berechnung erfolgt dann mit Hilfe dieser Bumpmap:

for(j = 1; j < SCREEN_Y - 1; j++)
	for(i = 1; i < SCREEN_X - 1; i++)
	{
		horizontal=
			heightmap[i + j * SCREEN_X - 1]-
			heightmap[i + j * SCREEN_X + 1];
		vertikal=
			heightmap[i + j * SCREEN_X - SCREEN_X] -
			heightmap[i + j * SCREEN_X + SCREEN_X];

		bumpmap[(i + j * SCREEN_X) * 2] = horizontal;
		bumpmap[(i + j * SCREEN_X) * 2 + 1] = vertikal;
	}
		

Die Berechnung des endgültigen Bildes unterscheidet sich nur in einer Kleinigkeit von der Berechnung der Lichtquelle in der ersten Ausgabe. Sie benötigen wie dort eine Shading-Tabelle und eine Lightmap.

Bevor Sie jedoch die Helligkeit für ein Pixel aus der Lightmap auslesen, modifizieren Sie die Koordinaten des Lightmap-Pixels durch Addition mit den horizontalen und vertikalen Neigungen der zu zeichnenden Pixel des Bildes. In C-Pseudocode würde das folgendermaßen aussehen:

for(j = 0; j < SCREEN_Y; j++)
	for(i = 0; i < SCREEN_X; i++)
	{
		//Wie bisher: addiere Bewegung der Lichtquelle
		xpos = i + horizontale_bewegung;
		ypos = j + vertikale_bewegung;

		//Der Unterschied:
		xpos = xpos + horizontale_neigung;
		ypos = ypos + vertikale_neigung;

		screen[i + j * SCREEN_X] =
			palette[lightmap[xpos +
			ypos * SCREEN_X * 2]]
			[bild[i + j * SCREEN_X]];
	}
		

Sie müssen bei der Modifikation der Koordinaten nur darauf achten, daß Sie stets in einem gültigen Wertebereich bleiben und nicht Speicher außerhalb der Lightmap adressieren.

Lensflares

Wenn Sie mit einer Videokamera gegen grelles Licht oder die Sonne filmen, können Sie hellere bunte Kreise oder n-Ecke im Bild beobachten. Diese Linsenfehler (Lensflares) entstehen durch Reflexion von sehr hellem Licht an den Linsen des Kamera­objektivs. Es ist unmöglich, solche Spiegelungen mathematisch und physikalisch korrekt in Echtzeit zu berechnen.

Für Demoeffekte nutzen Sie die Eigenschaften aus, die Sie in der Realität beobachten. Sie können einfach die Bildbereiche, an denen solche Linsenfehler auftreten, mit der Farbe dieser Erscheinung aufhellen. Die Lensflares liegen immer auf der Gerade, die vom Mittelpunkt des Bildes und der Position der Lichtquelle bestimmt werden. Die Position berechnen Sie aus dem Richtungs­vektor der Position der Lichtquelle zum Bild­mittelpunkt und einem konstanten Faktor für jeden Linsenfehler.

Programmieren Sie diesen Effekt als Zusatz zum Bumpmapping-Effekt. Dazu benötigen Sie gezeichnete (oder von einem Bild­bearbeitungs­programm berechnete) Bilder von Lensflares. Diese Bilder zeichnen Sie dann Pixel für Pixel auf den Bumpmapping-Effekt – so entsteht ein realistischer Effekt.

Doch zunächst definieren Sie einen Variablentyp:

typedef struct
{
	int sizebit, size;
	float faktor;
	bitmaptype bmp;
	int *map;
} lensflare;
		

Dabei ist size die Kantenlänge des quadratischen Bildes. Es sollen nur Zweierpotenzen als Größe möglich sein, also size = 2^sizebit Den Faktor für den Richtungs­vektor enthält faktor, die Zeiger auf das Bild sind bmp bzw. *map.

Die Bilder der Lensflares zeichnen Sie am besten in Graustufen. Die Farbe erhalten die Lensflares dann beim Laden des Bildes. Dabei gibt ein Faktor für Rot, Grün und Blau die Intensität des entsprechenden Farbkanals an.

Die Stelle, an der Sie den Lensflare zeichnen, erhalten Sie aus der Position der Lichtquelle auf dem Bild:

licht_x -= SCREEN_X / 2;
licht_y -= SCREEN_Y / 2;

lensflare_x = licht_x * faktor + SCREEN_X / 2 - size / 2;
lensflare_y = licht_y * faktor + SCREEN_Y / 2 - size / 2;
		

Setzen Sie den Lensflare an die berechnete Position. Dabei verwenden Sie die Technik des additiven Shadings (siehe Textbox, S. xxx) mit folgenden Befehlen:

//ofs ist die Adresse des Pixels im Bild
pixel = (screen[ofs] >> 1) & bitmask;

//mappos ist die Adresse des Lensflare-Pixels
flarepixel = flare.map[mappos];
screen[ofs] = remappalette[pixel + flarepixel];
		

Der Wassereffekt

Besonders faszinierend wirkt oft der Eindruck einer bewegten Wasser­oberfläche zwischen dem Bild und dem Betrachter. Dabei berück­sichtigen Sie neben der Licht­brechung durch das Wasser auch die Reflexion des Lichts einer beliebigen Lichtquelle. Dabei kann die Umsetzung auf einen in Echtzeit berechneten Effekt nicht physikalisch korrekt sein.

Zunächst benötigen Sie eine Repräsentation des Wassers. Hier bietet sich eine sogenannte Heightmap an, in der Sie für jedes Pixel den Wert für die Wasserhöhe speichern. Simulieren Sie nun die Schwingungen, die das Wasser vollzieht. Sie können sich dabei einen Wassertropfen vorstellen, der auf eine glatte Wasserfläche fällt. Sie sehen konzentrische Kreise, die sich langsam ausbreiten. Die Intensität der Schwingung läßt dabei mit der Zeit nach.

In Ihrem Programm verwenden Sie die beiden Heightmaps height1 und height2, mit deren Hilfe Sie ein Bild aus den vorhergehenden berechnen. Den Wert eines neuen Heightmap-Eintrags in height1 für die Position (X/Y) bestimmen Sie mit height2: Sie addieren die an diese Position in height2 anliegenden Höhen­informationen, teilen das Ergebnis durch 2 und subtrahieren die zu (X/Y) gehörende Höhe.

Sie erhalten einen neuen Höhenwert, den Sie nur noch abschwächen müssen, damit die Wellen auf dem Wasser tosen:

//Schwingung des Wassers
height1[X][Y] =
	((height2[X][Y - 1] +
	height2[X][Y + 1]+
	height2[X - 1][Y]+
	height2[X + 1][Y]) / 2)-
	height1[offset];

//Abschwächung
height1[X][Y] = height1[X][Y] * 0.875;
		

height1 enthält den aktuellen „Wasserstand“, mit dem Sie das fertige Bild zeichnen. Um die Reflexion und Lichtbrechung an einem Pixel zu berechnen, benötigen Sie eine Art Oberflächen­normale oder Ablenkung für das Wasser an diesem Punkt. Diese Ablenkung erhalten Sie getrennt für die Horizontale und die Vertikale:

ablenkung_h =
	height[X - 1][Y]-
	height1[X + 1][Y];
ablenkung_v=
	height[X][Y - 1]-
	height1[X][Y + 1];
		

Addieren Sie diese beiden Werte und eine Konstante, erhalten Sie einen Helligkeits­wert für eine von links oben scheinende Lichtquelle. Ändern Sie die Vorzeichen bei dieser Addition, ergibt sich eine andere Richtung des Lichts. Für einen Lichteinfall aus beliebiger Richtung multiplizieren Sie vor der Addition den einen Wert mit dem Sinus und den anderen mit dem Cosinus des Einfalls­winkels. Da Sie diese Operation allerdings für jedes Pixel benötigen, kostet das sehr viel Zeit.

Für die Beleuchtung zeichnen Sie jedes einzelne Pixel des Hintergrund­bildes mit der berechneten Helligkeit anhand einer Shading-Tabelle. Um die Lichtbrechung zu simulieren, addieren Sie zur X-Koordinaten die horizontale Ablenkung. Analog dazu rechnen Sie zur Y-Koordinaten die vertikale Ablenkung. Auf diese Weise erhalten Sie die Koordinaten des Pixels, das Sie auslesen und auf den Bildschirm schreiben:

helligkeit = ablenkung_h + ablenkung_v;
helligkeit += 128;

Xneu =X + (ablenkung_h);
Yneu =Y + (ablenkung_v);

screen[X][Y] = palette[helligkeit]
	[bild[Xneu][Yneu]];
		

Nachdem das Bild gezeichnet ist, müssen Sie nur noch die Speicher­bereiche von height1 und height2 vertauschen, damit die Berechnung des Wassers richtig funktioniert.

Was Ihnen jetzt noch fehlt, ist die Bewegung des Wassers. Dazu setzen Sie einfach an der Stelle, an der ein Tropfen auftreffen soll, den Wert in height1 auf einen festen Wert: water1[X][Y]=-1500; Sie sollten die Anzahl der Bilder pro Sekunde so reduzieren, daß alle Rechner damit fertig werden.

Ausblick

Sie haben nun eine Reihe von Bitmap-Effekten kennengelernt, die auf verschiedenen Techniken basieren. Bewegungs­unschärfe, Überblend­effekte, animierte Plasmawolken, Linsen- und Wassereffekte – damit lassen sich schon auf ganz einfache Art beeindruckende Effekte in eigenen Programmen erzeugen.

Es gibt allerdings noch weitere Möglichkeiten: In der nächsten Ausgabe werden Sie zwei weitere Arten kennenlernen, die durch geeignete Parameterwahl eine Vielzahl verschiedener Effekte zulassen.

Ihnen und Ihrer Kreativität sind bei der Arbeit keinerlei Grenzen gesetzt, da Sie durch leichtes Abändern der Algorithmen und durch Kombination verschiedener Verfahren spielend einfach neue, unglaubliche Effekte erzeugen.