Tanz der Bitmaps

Carsten Dachsbacher/Nils Pipenbrinck

Wir entwickeln in diesem Beitrag mit Hilfe von Movelists (Bewegungs­listen) den bekannten Tunneleffekt. Dieser stellt einen sich drehenden Tunnel (Zylinder) dar, in den der Betrachter beim Anschauen gleichsam magisch hineingezogen wird. Bei der Berechnung wird die Texturemap gewissermaßen um den Tunnel gewickelt.

Movelists sind Effekte, die eine oder mehrere Tabellen verwenden, um ein Bild aus einer Textur zu berechnen. Diese Tabellen geben an, in welchem Winkel oder welcher Entfernung sich ein Pixel zum Bildschir­mmittelpunkt befindet. Zudem legen sie die Helligkeits­werte für jedes Pixel fest. Beim Entwickeln einer Routine für diesen Effekt bestimmen Sie für jedes Pixel zuerst, welches Texel (Texture Pixel) der Textur gezeichnet werden soll. Anschließend legen Sie fest, welche sonstigen Attribute, wie zum Beispiel die Helligkeit, das Texel erhält.

Wenn Sie sich den Screenshot des Tunnels ansehen, können Sie beobachten, daß sich die Helligkeit des Tunnels von der Mitte nach außen hin erhöht. Damit haben Sie schon die Idee für die erste Movelist, die Sie hier benötigen. Da Sie bei diesem Effekt wieder mit einer 256-Farben-Textur arbeiten, empfiehlt es sich, für jedes Pixel direkt den Helligkeits­wert zu speichern, den eine Shading-Tabelle für die Textur verwendet. Der Helligkeits­verlauf in der Tabelle ist mit einer empirisch ermittelten Formel berechnet. Wie Sie sehen können, ist das für den räumlichen Eindruck auf jeden Fall ausreichend. Der folgende C-Code berechnet die Shading-Tabelle für den Tunnel:

// Shading-Tabelle für den Tunnel
offset = 0;
for(y = 0; y < SCREEN_Y; y++)
	for(x = 0; x < SCREEN_X; x++)
	{
		// Abstandsquadrate des Pixels
		// zur Bildschirmmitte
		xdist = SCREEN_X / 2 - x;
		ydist = SCREEN_Y / 2 - y;
		xdist *= xdist;
		ydist *= ydist;

		// Daraus wird ein Helligkeitswert berechnet
		d = 255.0 - sqrt(xdist + ydist);
		d *= d * d * d * d;
		d /= SCREEN_X * SCREEN_Y * 180.0 * 180.0;

		// auf den richtigen Wertebereich achten!
		d = min(255, max(0, d));
		// Und kleine Zufallswerte addieren,
		// um keine harten Kanten auftreten zu lassen
		d = (63 - d * 4.0) / 4.0 + rand() / 16384.0;
		stab[offset++] = d;
	}
		

Möglich wäre jetzt, eine Tabelle zu berechnen, die für jedes Pixel ein Texel bestimmt. Damit könnten Sie den Tunnel zwar darstellen, aber es würde sich nichts bewegen. Um den Tunnel um seine eigene Achse rotieren zu lassen und den Betrachter entlang des Tunnels zu bewegen, benötigen Sie zwei weitere Tabellen.

Die eine Tabelle, die für das Bewegen des Betrachters zuständig sein soll, enthält für jedes Pixel die V-Koordinate der Textur. Diese Tabelle soll noch von einem Abstandswert des Betrachters zur Zeichenebene und natürlich vom Radius des Tunnels abhängen. Wichtig ist, daß U und V für Textur­koordinaten stehen und X und Y für Bildschirm­koordinaten. Die Berechnung erfolgt folgendermaßen:

// V-Tabelle
offset = 0;
for(y = -SCREEN_Y / 2; y < SCREEN_Y / 2; y++)
	for(x = -SCREEN_X / 2; x < SCREEN_X / 2; x++)
	{
		if (x)
		// um Division durch 0 zu vermeiden
		{
			// Abstand berechnen
			temp = cos(atan((double)y / (double)x));
			temp *= abstand * radius / 8.0;
			if (temp == 0) temp ++;
			temp = fabs(temp/(double)x) + 64.0;
			ztab[offset++] = temp;
		} else
			// einfach den Wert des
			// Pixels daneben verwenden
			ztab[offset++] = temp;
	}
		

Die zweite Tabelle hält für jedes Pixel die U-Koordinate der Textur bereit. Da Sie die Textur um den Tunnel herumwickeln wollen, genügt es, bei dieser Tabelle für jedes Pixel den Winkel zu einer Halbgeraden (Strahl) aus dem Bildschirm­mittelpunkt zu bestimmen und diesen so zu skalieren, daß er die Breite der Texturemap hat. Diese Berechnung erledigen Sie mit dem Arcustangens:

// ArcTan-Tabelle
int offset = 0;
for(y = -SCREEN_Y / 2; y < SCREEN_Y / 2; y++)
		for(x = -SCREEN_X / 2; x < SCREEN_X / 2; x++)
		{
			if (x)
			// Division durch 0 vermeiden
			{
				// Winkel berechnen
				temp = atan((double)y / (double)x);
				// und auf die Breite der Textur skalieren
				temp = 256.0 * temp / 6.28318630718;
				// Vorzeichenkorrektur des Arctan
				if (x <= 0 && y <= 0)
					temp++;
				if (x > 0 && y > 0)
					temp++;
				if (x >= 0) temp += 128;

				atab[offset++] = temp;
		} else
			// Wert des vorherigen Pixels verwenden
			atab[offset++] = temp;
		}
		

Nachdem Sie alle diese Tabellen berechnet haben, geht es daran, den Tunnel zu zeichnen. Hierzu lesen Sie zuerst für jedes Pixel die dazugehörige U- und V- Koordinate aus. Damit können Sie das Texel aus der Texturemap auslesen. Wenn Sie aus der Shading-Tabelle für den Tunnel den Helligkeits­wert des Pixels ermitteln, können Sie der Textur den endgültigen Farbwert für das aktuelle Pixel zuweisen:

for(n = 0; n < SCREEN_X * SCREEN_Y; n++)
{
	u = atab[n];
	v = ztab[n];
	screen[n] = palette[stab[n]]
		[bmp[(v << 8)+u]];
}
		

Nun stellen Sie sich sicher die Frage, wie Sie Bewegung in den Tunnel bekommen. Sie haben die Textur um den Tunnel herumgewickelt, und zwar so, daß sie in der Breite genau einmal herumpaßt und sich in der Tiefe wiederholt. Dazu sollten Sie natürlich eine sogenannte seamless (saumlose) Textur verwenden, die Sie aneinander­legen können, ohne daß Kanten zu sehen sind.

Wenn Sie den Tunnel drehen wollen, addieren Sie einfach einen Wert auf die U-Koordinate. Damit ändern Sie den Drehwinkel, da der Winkel und die U- Koordinate aufgrund der Arcustangens- Tabelle direkt zusammenhängen. Sie müssen nur darauf achten, daß die Koordinaten, die über den Rand der Texturemap hinausgehen, am anderen Rand der Textur fortzusetzen sind.

Dies erreichen Sie dadurch, daß Sie den Rest ermitteln, der bei der Teilung von U-Koordinate und Texturemap- Breite entsteht. Wenn sie eine 256 Pixel breite Textur haben (wie hier), ergibt sich eine weitere Möglichkeit: Verknüpfen Sie sie mit AND 255, was deutlich schneller ist.

Der gleiche Trick wie bei der Drehung läßt sich analog auf die Bewegung entlang der Achse anwenden. Die Schleife zum Zeichnen des Tunnels sieht dann folgendermaßen aus:

for(n = 0; n < SCREEN_X * SCREEN_Y; n++)
{
	u = (atab[n] + drehung) & 255;
	v = (ztab[n] + bewegung) & 255;
	screen[n] = palette[stab[n]]
		[bmp[(v >> 8) + u]];
}
		

Wie Sie sehen, ist die Berechnung von komplexen Effekten mit Hilfe von Movelists sehr einfach und auch sehr schnell. Mit wenigen Speicher­zugriffen pro Pixel erhalten Sie Bilder, die Sie mit 3D-Routinen nicht in dieser Geschwindig­keit berechnen können. Und auf heutigen Rechnern fällt der Speicherbedarf für die Tabellen auch nicht mehr ins Gewicht.

Ein weiterer Vorteil dieser Methode ist es, daß die Berechnung trotz der wenigen Register der Pentium- und Pentium-kompatiblen Prozessoren parallelisiert werden kann. Dies können Sie in der im Quelltext enthaltenen Assembler-Schleife sehen, in der zwei Pixel pro Schleifen­durchlauf berechnet werden und der Prozessor deshalb optimal ausgenutzt wird.

Freies Verzerren von Bitmaps

Die zweite Methode ist ein sehr einfaches und schnelles Verfahren, um Bitmaps zu verzerren. Diese Methode arbeitet ähnlich wie die bereits vorgestellte Tunnelmethode. Um die aufwendige Berechung von Textur­koordinaten zu verkürzen bzw. um auf große Tabellen zu verzichten, benutzen Sie einen Trick:

Sie unterteilen den Bildschirm in kleinere Bereiche, die genau 8 x 8 Pixel groß sind. So erhalten Sie ein Gitter, für dessen Kreuzungs­punkte (die Ecken der 8 x 8-Pixel-Blöcke) Sie die genauen Textur­koordinaten für das Bild berechnen.

Angenommen, Sie arbeiten in einer Auflösung von 320 x 240 Punkten. Dann müssen Sie nur (320/8)+1=41 Koordinaten auf der X-Achse und (240/8)+1 Koordinaten auf der Y-Achse berechnen. Insgesamt macht das nur 1271 Textur­koordinaten. Im Vergleich dazu: Berechnen Sie die Textur­koordinaten für jedes Pixel einzeln, dann sind es 76 800 Berechnungen. Mit einem einfachen Trick erreichen Sie also allein für die Berechnung etwa eine Beschleunigung um den Faktor 60.

Wo liegt der Vorteil gegenüber der Tunnelmethode? Sie können für jedes Bild die Textur­koordinaten völlig neu berechnen, da der Aufwand sehr gering ist, und damit abhänging von der Zeit den Effekt sehr flexibel gestalten.

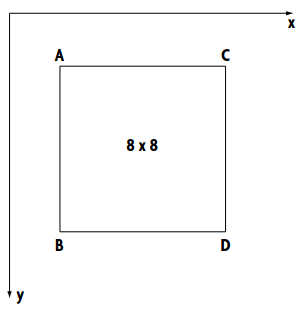
Nun zeichnen Sie mit Ihren Koordinaten natürlich auch etwas. Sie werden sehen, daß dies viel einfacher ist, als es im ersten Moment aussieht. Das Gitter, das Sie berechnen, besteht – wie bereits erwähnt– aus vielen kleine Kästchen, die alle 8 x 8 Pixel groß sind.

Sie berechnen das endgültige Bild, indem Sie jeden 8 x 8-Block mit einer Textur füllen. Die Textur­koordinaten entnehmen Sie den vier Eckpunkten und interpolieren über den Block linear. Nun sehen Sie, daß Sie, um beispielsweise 320/8=40 Blöcke zu zeichnen, 41 Stützwerte benötigen, damit Sie die Textur­koordinaten auch für den letzten Block erhalten.

Ein Texture-Mapper für 8 x 8-Blöcke

Diese Routine entwickeln wir, um die Textur für einen Block zu interpolieren. Im Gegensatz zum normalen Texture- Mapping ist die Interpolation von Texturen über 8 x 8-Blöcke sehr einfach: Es ist nicht nötig, die aufwendige Kanten­berechnung für die Polygone durchzuführen. Auch fallen sehr rechen­intensive Operationen wie etwa die Division für die Inkremente weg, da die Breiten und Höhen der Kästchen immer acht Pixel weit sind. Divisionen von Zweierpotenzen lassen sich durch schnellere Shift-Operationen ersetzen.

Wie beim Texture-Mapping üblich, arbeiten Sie mit Fixed-Point-Zahlen (vergleiche PC Underground, PC Magazin 8/98, ab S. 234). Zunächst einmal interpolieren Sie die Textur­koordinaten der linken und rechten Kante des Kästchens. Über die während der Interpolation entstehenden linken und rechten Textur­koordinaten zeichnen Sie dann später eine acht Pixel lange Zeile, um den Zwischenraum zu füllen.

Die folgende Struktur enthält die Koordinaten eines Gitterpunkts:

struct GridPointUV
{
	signed int u;
	signed int v;
}

GridPointUV a,b,c,d;

signed int dudy_left = (b.u - a.u) / 8;
signed int dvdy_left = (b.v - a.v) / 8;
signed int dudy_right= (d.u - c.u) / 8;
signed int dvdy_right= (d.v - c.v) / 8;
		

Die vier signed-int-Werte sind die vertikalen Koordinaten­inkremente. Die Namen der Variablen haben einen guten Grund: Sie sind der Mathematik entliehen. dudy bedeutet, daß diese Variable die Steigung der U-Koordinate (Textur) entlang der Y-Koordinate (Bitmap) ist. Das _left und _right bezieht sich auf die Kante des Blocks.

Die Interpolation über die vertikalen Kanten eines Blocks implementieren Sie wie folgt:

GridPointUV left = a;
GridPointUV right = b;
for(int y = 0; y < 8; y++)
{
	// Zeichnen einer Zeile (siehe unten)

	// Anpassen der left- und right-
	// Variablen für die nächste Zeile
	left.u += dudy_left;
	left.v += dvdy_left;
	right.u += dudy_right;
	right.v += dvdy_right;
}
		

Das Zeichnen der Zeile selbst ist fast identisch mit der Berechnung der vertikalen Kanten. Erneut werden die Steigungen (diesmal für die X-Achse) entlang der Bildschirm­zeile berechnet, und dann die Interpolations­variablen initialisiert und gezeichnet:

dudx = (right.u - left.u) / 8;
dvdx = (right.v - left.v) / 8;
signed int u = left.u;
signed int v = left.v;
for(int x = 0; x < 8; x++)
{
	// Umwandlung von Fixed-Point in echte Koordinaten
	// In diesem Beispiel geht die
	// Routine von 256*256 großen Texturen aus.
	int texel_u = ((u>16) & 0x00ff);
	int texel_v = ((v>16) & 0x00ff);

	// Lesen von Texture-Pixel bei
	// [texel_u][texel_v] ...)
	//... setzen des Pixels bei
	// [x][y] ...)

	// Anpassen der u- und
	// v-Variablen für das nächste
	// Pixel
	u += dudx;
	v += dvdx;
}
		

Wenn Sie sich nach dem Download die komplette Routine im Quelltext von grid.cpp ansehen, stellen Sie fest, daß diese Routine sehr einfach geschrieben ist, aber dennoch rasend schnell läuft, da auf aufwendige Berechnungen verzichtet werden kann.

Die Routine zum Zeichnen der 8 x 8- Blöcke ist so schon ganz praktisch. Damit Sie aber wirklich bequem Effekte ausprobieren können, brauchen Sie noch eine Routine, mit der Sie den kompletten Bildschirm mit den Textur­koordinaten aus einem vollständigen Gitter zeichnen:

void RenderScreen8x8
	(GridPointUV *gitter,
	// Gitter-Array
	unsigned short *dest,
	// Pointer auf das Bitmap
	unsigned short *palette,
	unsigned char *texture)
{
	// Anzahl der Blöcke:
	long BlocksX = SCREEN_X / 8;
	long BlocksY = SCREEN_Y / 8;

	// Pointer auf die Koordinaten der aktuellen Zeile
	GridPointUV *line = gitter;
	// Pointer auf die Koordinaten der nächsten Zeile
	GridPointUV *nextline = &gitter[BlocksX + 1];

	// Schleife über alle Zeilen:
	for(int y = 0; y < BlocksY; y++)
	{
		// eine Zeile von 8x8
		// Kästchen Zeichnen:
		for(int x = 0; x < BlocksX; x++)
			Render8x8Block(line[x + 0],
				nextline[x + 0],
				line[x + 1],
				nextline[x + 1],
				&dest[x * 8],
				SCREEN_X,
				palette,
				texture);
		// Variablen für nächste
		// Zeile anpassen
		dest += SCREEN_X * 8;
		line = nextline;
		nextline += (BlocksX + 1);
	}
}
		

Der Roto-Zoomer

Ein Roto-Zoomer ist ein Effekt, der eine Textur gleichzeitig dreht und vergrößert bzw. verkleinert. Vor einigen Jahren war dieser Effekt bei Demo-Programmierern sehr beliebt, um Programmier­fähigkeiten zu zeigen.

Roto-Zoomer sind mit dem vorgestellten Algorithmus sehr einfach zu berechnen. Die Routine ist dann beinahe so schnell, daß der Hauptspeicher die ankommenden Pixeldaten nicht schnell genug speichern kann und zur Bremse wird.

Für diesen Effekt berechnen Sie die gedrehten und gezoomten Textur­koordinaten U und V für jeden Gitterpunkt. Dies erledigen Sie am besten mit folgendem Programmcode – das Beispiel ist für eine Auflösung von 320 x 240 ausgelegt:

GridPointUV Gitter[41][31];
float rotation;
float zoomfaktor;

// Vorberechnen der Rotation und der Skalierung
float cosinus = cos(rotation) * zoomfaktor;
float sinus = sin(rotation) * zoomfaktor;

// Zwei Schleifen zum Berechnen des Gitters
for(int hoehe = 0; hoehe < 31; hoehe++)
	for(int breite=0; breite < 41; breite++)
	{
		// Berechnen von x und y
		// relativ zum Bildschirmmittelpunkt:
		float x = ((float)breite - 20.0);
		float y = ((float)hoehe - 15.0);

		// Berechnen von u und v
		// durch einfache Rotation.
		// 65536 ist die Skalierung
		// für die Fixed-Point-Umwandlung
		Gitter[y][x].u = (x * sinus - y * cosinus) * 65536.0;
		Gitter[y][x].v = (y * sinus + x * cosinus) * 65536.0;
	}
		

Anschließend durchlaufen Sie eine weitere Schleife und rufen die 8 x 8-Texture-Mapping-Routine für jedes Kästchen auf.

Noch mehr Effekte

Wie Sie sehen, haben Sie mit dieser Routine bereits einen Effekt-Baukasten. Den Möglichkeiten sind (fast) keine Grenzen gesetzt. Sie können wilde mathematische Formeln benutzen, um Textur­koordinaten zu berechnen. Überlagern Sie zum Beispiel einfach ein paar Sinus­funktionen, und schon fängt Ihre Textur an, sich wild zu verzerren.

Diese Routine ist natürlich nicht auf Texturen beschränkt. Sie können auch Farben über die Blöcke hinweg interpolieren. Ändern Sie dazu die Interpolation auf die drei Farb­komponenten R,G und B ab. Am mathematischen Teil ändert sich dadurch nichts. Sie können auf diesem Weg ein Sinus-Plasma zeichnen, das um ein Vielfaches schneller läuft als mit der in der vorigen Ausgabe vorgestellten Methode.

Viele schöne Effekte erreichen Sie durch Projektion. Dabei berechnen Sie aus den X- und Y-Koordinaten und einer Tiefen­koordinate Z die Textur­koordinaten. Die Umrechnung in U/V-Koordinaten erfolgt durch einfache perspek­tivische Projektion.

U = x * perspektive / z;
V = y * perspektive / z;
		

In den Beispiel-Codes ist ein Effekt implementiert, der mit dieser Methode arbeitet (siehe Bild oben).

Sie können auch zwei Effekte gleichzeitig berechnen und die Textur­koordinaten von einem Effekt in den anderen überblenden. Hierbei ist allerdings Vorsicht geboten: Die 8 x 8-Interpolation funktioniert immer nur in eine Richtung. Sobald die Routine einen Wrap- Around ausführen muß, wird sie versagen.

Ein kleines Beispiel hierzu: Die linke U-Koordinate beträgt 255, während die rechte Koordinate 10 ist. Dies führt zu einer Steigung von (255-10)=245. Das bedeutet, daß fast die gesamte Textur rückwärts in das Kästchen gemappt wird. Leider ist dieses Ergebnis falsch, da Sie ja immer mit seamless (kantengleichen) Texturen arbeiten.

Wenn Sie diesen Fall vermeiden wollen, dann können Sie den 8 x 8-Interpolierer so umschreiben, daß im Gitter keine Textur­koordinaten, sondern die Steigung direkt gespeichert wird. Viele Effekte (besonders Sinus-Verzerrer und Plasmen) lassen sich auch so berechnen. Direktes Berechnen der Textur­koordinaten ist jedoch viel anschaulicher und einfacher.

Erweiterung auf Lichteffekte

Es gibt einen weiteren Weg, das vorher genannte Problem zu umgehen. Mit einem neuen Feature interpolieren Sie zusätzlich zu den Textur­koordinaten noch eine Helligkeit. Diese Helligkeit berechnen Sie dann so, daß die Stellen in der Bitmap dunkel sind, die durch die hohen Steigungen unschön ausehen, während die guten Teile der Textur normal erscheinen.

Ändern Sie hierfür die Struktur des GridPointsUV ab, und fügen Sie einen Hellig­keitswert hinzu. Die Variable bezeichnen Sie nach dem bekannten Gouraud-Shading mit g, da Sie im Prinzip hier nichts anderes machen.

struct GridPointUVG
{
	signed int u;
	signed int v;
	signed int g;
}
		

Sie passen natürlich noch die Routinen zum Zeichnen an. Wie bei den R-, G- und B- Koordinaten ist es eine einfache Erweiterung. Sie kopieren einfach den Code von U oder V. Im Beispiel-Code haben wir dies schon für Sie vorbereitet.

Zum Beleuchten der Texturen sollten Sie wie bei den bisherigen Effekten die Textur in 8 Bit Farbtiefe pro Pixel (256 Farben) vorliegen haben. Sie können dann zur Textur eine Shading-Palette mit (bei diesem Effekt) 256 Schattierungen berechnen und die jeweilige Schattierung anhand des Gouraud-Hellig­keitswerts auswählen.

Die Berechnung der Shading-Palette ist sehr einfach. Angenommen, Sie möchten eine einfache Beleuchtung haben, dann reservieren Sie sich genug Speicher für diese Tabelle. Sie benötigen für jede Palette 512 Byte (256 Farben à 2 Byte, da ein Pixel 2 Byte groß ist), und da Sie 256 Schattierungen anlegen, liegt der Speicherbedarf insgesamt bei 128 KByte. Wenn Sie weniger Speicher für die Tabelle verwenden möchten, dann beschränken Sie sich auf 32 Schattierungs­stufen. Dies liefert nicht ganz so gute Ergebnisse, doch wird das Programm dadurch etwas schneller.

Dies liegt an dem Problem der Intel- Prozessoren, deren Zugriffe auf Speicher­bereiche, die weit auseinander liegen, relativ langsam sind. Verantwortlich dafür ist, daß der Prozessor-Cache nicht so viele Werte zwischen­speichern kann. Deshalb wird der Cache vom System vergeblich durchsucht, was zusätzlich Rechenzeit kostet.

Die Shading-Tabelle berechnen Sie mit einer doppelt geschachtelten Schleife, die jede Farbe einzeln ermittelt. Genau dies erledigt die Routine MakeShadedPalette in der Datei grid.cpp. Zum Verständnis hier der wichtigste Code-Teil:

for(int Shading = 0; Shading < 256; Shading++)
	for(int Index = 0; Index < 256; Index++)
	{
		// Shading von Rot, Grün und Blau
		int r = (Bitmap->cColors
			[Index * 4 + 0]*Shading) / 256;
		int g = (Bitmap->cColors
			[Index * 4 + 1]*Shading) / 256;
		int b = (Bitmap->cColors
			[Index * 4 + 2]*Shading) / 256;

		// Zusammensetzen der
		// 16-Bit-Farbe
		Palette[Shading * 256 + Index] =
				Rtab[r]|Gtab[g]|Btab[b];
	}
		

Sie können auch zusätzlich bei den hellsten Schattierungs­stufen weiße Farbanteile auf die RGB-Werte addieren. Dann bekommen Sie wunderschöne Glanzlichter auf die Effekte. Oder Sie interpolieren zum Beispiel zwischen zwei Paletten und geben damit den Effekten einen ganz neuen Charakter. Den Möglichkeiten sind auch hier keine Grenzen gesetzt.

König der 2D-Effekte

Zum Abschluß nun noch der König der 2D-Effekte: die Feedbacks (Rückkoppelungs­effekte). Sie entstehen, wenn Sie ein berechnetes Bild als neue Textur für das nächste Bild verwenden. Damit erzeugen Sie sehr interessante Effekte. Das Problem bei diesen Feedback-Effekten ist, daß sie sich zwar sehr einfach aus 8x8-Mappern herleiten lassen, aber sehr schwer in den Griff zu bekommen sind.

Im Pseudo-Code ist die Erstellung eines Feedbacks sehr einfach:

do {
		Verforme Textur
		in eine Bitmap;
		Kopiere Bitmap
		in die Textur;
		Zeige Bitmap
		auf dem Screen;
	} while
(!Langeweile)
		

Das Problem mit Feedbacks ist, daß die Textur nach und nach vollständig zerstört wird – dies geschieht durch die wiederholte Verzerrung. Entweder erhalten Sie nach einiger Zeit eine einfarbige Bitmap oder Sie haben nur noch buntes Rauschen auf dem Bildschirm.

Diese Probleme können Sie in den Griff bekommen: Restaurieren Sie nach jedem Durchlauf einen Teil des Bildes. So vermeiden Sie am Ende einen einfarbigen Bildschirm. Sie können beispielsweise immer einen Teil einer Bitmap über die neue Textur kopieren, die Sie erhalten haben.

Das Rauschen ist ebenfalls mit einem einfachen Trick zu bewältigen: Wie in der vorigen Ausgabe von PC Underground beschrieben, läßt sich mit einem Motionblur-Algorithmus das aktuelle und das letze Bild in einem Verhältnis von 50 Prozent mischen.

Hiermit haben Sie alles, was Sie zum Experi­mentieren benötigen. Mit den Effekt­baukästen, die Sie nun kennen, können Sie eine große Vielzahl von Bitmap- Effekten berechnen, die Sie allesamt in einer modernen Demo finden können – und vielleicht schon bald in Ihrer Demo.