Welten aus Lichtstrahlen

Carsten Dachsbacher/Nils Pipenbrinck

Raytracing berechnet eindrucksvolle Bilder einer mathematischen Welt. Diese künstliche Welt basiert auf der Idee, einen Lichtstrahl zurückzu­verfolgen, der eine imaginäre Kamera erreicht.

Die Lichtstrahlen können zum Beispiel auf Objekte treffen, deren Material Licht absorbiert, reflektiert bzw. teilweise oder ganz hindurchläßt. Andere Materialien wiederum kombinieren beliebige dieser Eigenschaften.

Prinzip des rekursiven Raytracing

Stellen Sie sich vor, daß ein Strahl, den Sie zurück­verfolgen, sich eventuell an einer Oberfläche teilt. Da ein Teil seines Lichts absorbiert, ein anderer Teil reflektiert wird, liegt es nahe, Raytracing rekursiv zu berechnen, also eine Berechnung zu wählen, die sich selbst wieder aufruft. Das Problem, festzustellen, an welcher Oberfläche der Lichtstrahl auftrifft, hört sich unbedeutend an, ist aber der rechen­intensivste Teil der Raytracing-Methode.

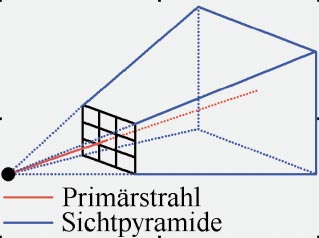
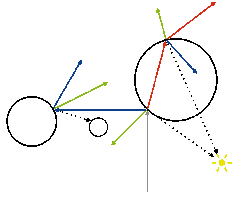
Wie sich Strahlen aufteilen können, sehen Sie in einer Aufsicht auf drei Kugeln. Der graue Primärstrahl fällt auf die Szene, blau reflektieren die Sekundär­strahlen. Rot symbolisierte Strahlen entstehen durch Lichtbrechung und Transparenz.

Die grün einge­zeichneten Vektoren sind die Oberflächen­normalen: Diese kennzeichnen jeweils den Vektor, der senkrecht auf einem Punkt der Oberfläche steht. Mit den Normalen berechnen Sie später die Beleuchtung. Die gepunkteten Linien heißen Schatten­strahlen.

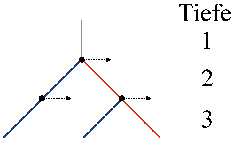
Da die Berechnung rekursiv erfolgt, sich also selbst wieder aufruft, unterscheiden Sie verschiedene Rekursions­tiefen. Diese verwenden Sie hauptsächlich, um die Berechnungen an einer bestimmten Tiefe abzubrechen. Stellen Sie sich vor, Sie verfolgen einen Lichtstrahl, der zwischen zwei perfekten Spiegeln hin- und herreflektiert wird. Die Berechnungs­routine würde sich immer wieder selbst aufrufen und nie stoppen.

Darum legen Sie bei Raytracing eine maximale Rekursions­tiefe fest: Sie verfolgen einen Lichtstrahl nur bis zu einer bestimmten, festgelegten Spiegelung. Die Berechnungs­routine veran­schaulicht der Pseudocode raytrace.rechne (Listing 1).

Mathematische Grundlagen

Mathematische Grundlagen führen tiefer in das Thema hinein. Punkte im drei­dimensionalen Raum geben Sie durch Ihre x-, y- und z-Komponenten an. Den Vektor x⃗ beschreiben Sie also mit x⃗ = (x1, x2, x3) Mit einem Vektor bestimmen Sie einen Ort (Ortsvektor) oder legen eine Richtung fest. Aus einem Startpunkt s⃗ und einer Richtung r⃗ definieren Sie mit t als reeller Zahl eine Gerade eindeutig im Raum: x⃗ = s⃗ + r * r⃗ Wenn zusätzlich t > 0 gilt, handelt es sich um eine Halbgerade, also um den Teil der Geraden, der vom Antragspunkt aus dem Richtungs­vektor folgt. Diese Rechnungen operieren mit Vektoraddition und Subtraktion: x⃗ + y⃗ = (x1 + y1, x2 + y2, x3 + y3) x⃗ - y⃗ = (x1 - y1, x2 - y2, x3 - y3) Für weitere Berechnungen benötigen Sie den Betrag eines Vektors, also seine Länge. Diese berechnen Sie mit der drei­dimensionalen Variante nach Pythagoras: |x⃗| = sqrt(x1 * x1 + x2 * x2 + x3 * x3) Zusätzlich benötigen Sie das Skalarprodukt, wofür Sie das Zeichen * definieren: x⃗ * y⃗ = x1 * y1 + x2 * y2 + x3 * y3 Sie erhalten also aus zwei Vektoren eine reelle Zahl. Das Skalarprodukt bringt noch weitere Eigenschaften mit: x⃗ * y⃗ = |x⃗| * |y⃗| * cos(phi) phi stellt dabei den Winkel zwischen den beiden Vektoren dar. Mit dem Skalarprodukt berechnen Sie auch die Beleuchtung.

Die letzte Vektor­operation ist das Vektor- oder Kreuzprodukt. Wenn Sie zwei Vektoren mit dem Vektorprodukt verknüpfen, erhalten Sie einen dritten Vektor, der senkrecht auf der von den zwei Vektoren aufgespannten Ebene steht. Es gilt: x⃗ X y⃗ = (x2*y3-x3*y2, x3*y1-x1*y3, x1*y2-x2*y1)

Eine weitere Grundlage für dieses Raytracer-Projekt ist die Matrizen­rechnung. Stark vereinfacht können Sie eine Matrix als einen Kasten voller Zahlen bezeichnen, der verknüpft mit einem Vektor eine geometrische Transformation darstellt. Solche Transform­ationen können zum Beispiel Drehungen, Verschiebungen oder Skalierungen sein.

Durch Multiplikation zweier Matrizen erhalten Sie eine neue Matrix, die die beiden Transforma­tionen der Ausgangs­matrizen enthält. Dabei ist die Reihenfolge natürlich entscheidend, denn es macht einen Unterschied, ob Sie einen Vektor zuerst drehen und dann verschieben – oder umgekehrt.

An dieser Stelle konzentrieren Sie sich lediglich auf die Anwendung von Matrizen. Im Sourcecode des Raytracers finden Sie alle entsprechenden Routinen, die Sie zur Matrizen­rechnung benötigen. Wenn Sie eine Matrix einfach als Transformation ansehen, können Sie diese Routinen verwenden, ohne sich länger mit der Theorie beschäftigen zu müssen.

Das Kameramodell

Die virtuelle Kamera ist eine erste Anwendung der Matrizen­rechnung. Für die einfachere Berechnung der Primärstrahlen soll die Kamera immer auf der negativen z -Achse des Koordinaten­systems liegen. Da sie aber frei positionierbar sein soll, müssen sich die anderen Objekte in der mathematischen Welt entsprechend bewegen.

Sie bewegen und drehen die mathematische Welt also so, daß die Kamera auf der z -Achse steht. Die Berechnungs­schritte dazu finden Sie in der Routine rtcamera.cpp auf der Heft-CD in der Funktion ab Zeile 314:

RTCamera :: BuildMatrix()
		

Wenn Sie eine Kamera durch eine Position und einen Punkt, auf den Sie zeigt, festgelegt haben, arbeiten Sie drei Schritte ab:
• Sie berechnen die Verschiebungs­matrix, damit der Zielpunkt in den Ursprung „rutscht“.
• Sie berechnen die Drehungsmatrix, um den Startpunkt auf die z-Achse zu rotieren, wobei Sie um den Zielpunkt drehen.
• Sie multiplizieren die Matrizen.

Das Resultat transformiert alle in der mathematischen Welt vorhandenen Ortsangaben, also die Ortsvektoren.

Alle Ortsangaben beziehen sich nun auf die neue mathematische Kameraposition. Diese befindet sich auf einem beliebigen Punkt wie (0,0,-z) und blickt in Richtung des Ursprungs (0,0,0).

Mit diesem Wissen und einem gegebenen Öffnungswinkel der Sichtpyramide berechnen Sie die Primärstrahlen:

float Breite = tan(OeffnungswinkelHorizontal);
float Hoehe = tan(OeffnungswinkelVertikal);
for(y = 0; y < Zeilen; y++)
	for(x = 0; x < Spalten; x++)
	{
		PixPos.x = ( 2 * x /
			Bildschirmbreite - 1) * Breite * (-z)
		PixPos.y = (2 * y /
			Bildschirmhoehe - 1) * Hoehe * (-z)
		PixPos.z = 0;
		Ray = PixPos - (0, 0, -z)
		Pixel(x, y) = Raytrace(Ray, 1)
	}
		

Schnittpunkt­berechnung

Die Schnittpunkt­berechnungen sind der wichtigste und rechenzeit­aufwendigste Teil eines Raytracers. Es gilt also, diese möglichst effizient zu berechnen und ihre Zahl klein zu halten.

Bei den folgenden Herleitungen gehen Sie immer davon aus, daß Sie eine Halbgerade durch ihren Startpunkt g⃗ und ihren Richtungs­vektor dg⃗ → bestimmen. Sie können also die Geraden­gleichung mit t als beliebiger Zahl aufstellen: x⃗ = g⃗ + t * dg⃗ Für die Halbgeraden gilt wieder t > 0

Die Ebene

Das einfachste geometrische Primitiv für einen Raytracer ist die Ebene: Sie stellen also fest, ob ein Strahl eine Ebene schneidet. Eine Ebene im Raum legen Sie eindeutig durch drei (Antrags-) Punkte fest. Diese Darstellung haben wir zur Eingabe in der Skriptsprache gewählt.

Für das Raytracing-Programm überführen Sie diese Darstellung in die sogenannte Hessesche Normalform (HNF). Diese verwendet die Normale auf einer Ebene und ihren Abstand zum Koordinaten­ursprung. Ist die Ebene durch die Punkte x1⃗, x2⃗ und x3⃗ gegeben, so erhalten Sie die Normale mit folgender Formel:

a⃗ = x2⃗ - x1⃗
b⃗ = x3⃗ - x1⃗
n⃗ = a⃗ X b⃗
		

Nach dem Kreuzprodukt X müssen Sie die Normale noch normalisieren, das heißt sie auf die Länge 1 bringen. Dazu teilen Sie jede Komponente von n⃗ durch ihren Betrag.

Den Abstand der Ebene vom Ursprung erhalten Sie, indem Sie einen beliebigen Antragspunkt auf die Normale projizieren. Diesen Vorgang erledigen Sie mit dem Skalarprodukt: abstand = n⃗ * x1⃗ Das Resultat dieser Vorberech­nungen verdeutlicht eine Formel, in der alle Punkte x⃗, die sich auf dieser Ebene befinden, folgende Gleichung erfüllen: n⃗ * x⃗ = abstand (HNF) Der mathematische Trick ist nur, das x⃗ in der HNF durch die Geraden­gleichung zu ersetzen. Sie erhalten dann n⃗ * (g⃗ + t * dg⃗) = abstand Alle Parameter außer t sind Ihnen in dieser Gleichung bekannt. Durch das t können Sie den Schnittpunkt bestimmen. Also lösen Sie die Gleichung nach t auf:

n⃗ * g⃗ + n⃗ * t * dg⃗ = abstand
t * n⃗ * dg⃗ = abstand - n⃗ * g⃗
t = (abstand - n⃗ * g⃗) / (n⃗ * dg⃗)
		

Die Gerade hat nur einen Schnittpunkt mit der Ebene, wenn der Term (n⃗ * dg⃗) ungleich Null ist. Andernfalls könnten Sie die Gleichung auch nicht lösen, da eine Division durch Null vorläge.

Setzen Sie das soeben berechnete t wieder in die Gleichung ein, erhalten Sie den Schnittpunkt: s⃗ = g⃗ + t * dg⃗ Dieser ist nur interessant, wenn t > 0 ist, da er sich sonst auf der „falschen“ Seite der Halbgeraden befindet, also zum Beispiel hinter dem Betrachter.

Die Kugel

Das zweite Primitiv, das wir Ihnen in diesem ersten Teil des Raytracers vorstellen, ist die Kugel. Eine Kugel legen Sie durch Mittelpunkt und Radius fest. Der Radius ist der Abstand vom Mittelpunkt. Also müssen alle Punkte auf der Kugel­oberfläche, welche für uns von Interesse sind, diesen Abstand vom Kugel­mittelpunkt haben. Den Abstand zweier Punkte im Raum berechnen Sie mit

a⃗ = (ax, ay, az)
b⃗ = (bx, by, bz)
abstand = sqrt(ax * bx + ay * by + az * bz)
	= sqrt(a⃗ * b⃗)
		

Wenn Sie also die Kugel durch ihren Mittelpunkt m⃗ und ihren Radius r definiert haben, erfüllen alle Punkte x⃗ auf ihrer Oberfläche die Gleichung sqrt(d⃗ * d⃗) = radius Der Vektor d⃗ geht vom Mittelpunkt zum variablen Punkt x⃗: d⃗ = (m⃗ - x⃗) Daraus ergibt sich: sqrt((m⃗ - x⃗) * (m⃗ - x⃗)) = radius Bei dieser Gleichung können Sie nicht einfach die Wurzel mit dem vermeintlich quadratischen Term darunter auflösen.Denn (m⃗ - x⃗) stellt einen Vektor dar, während (m⃗ - x⃗) * (m⃗ - x⃗) eine reelle Zahl ist.

Auch in dieser Gleichung müssen Sie x⃗ ersetzen, um den Schnittpunkt zu erhalten, aber vorher quadrieren Sie sie:

(m⃗ - x⃗) * (m⃗ - x⃗) =
	(m⃗ - x⃗)2=radius2
	(m⃗ - (g⃗ + t * dg⃗))2
	= radius2
	((m⃗ - g⃗) - t * dg⃗)2
	= radius2
	(m⃗ - g⃗)2 - 2 * (m⃗ - g⃗)
* (t * dg⃗) + (t * dg⃗)2
= radius2
		

Diesen Term formen Sie nun in eine quadratische Gleichung um, zu der es eine Lösungsformel gibt:

t2 * dg⃗2 -
t * (m⃗ - g⃗) * dg⃗ +
(m⃗ - g⃗)2 - radius2 = 0
		

oder a*t² + b*t + c = 0 mit

a = dg⃗2
b = -(m⃗ - g⃗) * dg⃗
c = (m⃗ - g⃗)2 - radius2
		

a, b und c sind reelle Zahlen. Die möglichen Lösungen sind dann

t1 = (-b + sqrt(b2 - 4 * a *c)) / (2 * a);
t2 = (-b - sqrt(b2 - 4 * a *c)) / (2 * a);
		

Die Zahl der Lösungen läßt sich durch die Diskriminante D = b² - 4 * a * c bestimmen. D < 0 bedeutet keine Lösung, D = 0 eine Lösung und D > 0 zwei Lösungen.

Diese t1 und t2 , eingesetzt in die Gleichung der Halbgeraden, ergeben dann wieder einen oder mehrere Schnittpunkte.

Wie Sie im folgenden sehen, benötigen Sie beim Raytracing auch immer die Oberflächen­normale an einem Schnittpunkt. Bei der Ebene steht diese immer fest. Bei der Kugel erhalten Sie sie, indem Sie die Differenz des Ortsvektors eines Schnittpunkts und des Kugelmittel­punkts normalisieren, also: der normalisierte Vektor zu (s⃗ - m⃗).

Natürlich benötigen Sie im Raytracing-Programm nur die endgültigen Formeln, die aber ohne ihre Herleitung kaum nachvoll­ziehbar sind. Wie Sie sehen, sind einige geschickte Umformungen notwendig, die zudem Rechenzeit sparen. Deshalb speichert jedes Raytracing-Programm zum Beispiel zu einem Kugelobjekt nicht nur den Radius, sondern auch gleich dessen Quadrat. Denn nur damit rechnet das Programm.

Beleuchtung berechnen

Nachdem Sie nun Schnittpunkte berechnen können, bleibt noch der zweite wichtige Punkt des Raytracing: die Berechnung der Beleuchtung. Diese Rechen­verfahren klären, wie sich das einfallende Licht und die Oberflächen­eigenschaften auf den visuellen Eindruck auswirken.

Der erste Einfluß­parameter ist das sogenannte ambiente Licht, ein überall in der mathematischen Welt gleichstarkes Licht. Dieses läßt die Oberfläche der Körper überall in ihrer Eigenfarbe erscheinen.

Bei den folgenden Berechnungen für die Beleuchtung müssen Sie vorher für jeden Schnittpunkt feststellen, ob und wie stark er von den Lichtquellen bestrahlt wird. Der einfachste Fall einer Lichtquelle – und der vorerst hier verwendete – ist eine punktförmige Lichtquelle ohne räumliche Ausdehnung.

Um festzustellen, ob eine Lichtquelle einen Punkt beleuchtet, berechnen Sie einen sogenannten Schattenstrahl. Dieser stellt eine Halbgerade vom Schnittpunkt in Richtung der Lichtquelle dar.

Nun berechnen Sie die Schnittpunkte der Objekte mit dem Schattenstrahl. Wenn es Schnittpunkte mit undurch­sichtigen Objekten gibt, liegt der Schnittpunkt im Schatten, bei teilweise durchsichtigen Objekten vermindern deren Transparenz und Farbe das Licht der Quelle.

Wenn nun eine Lichtquelle einen Punkt beleuchtet, kommen noch zwei weitere Eigenschaften hinzu, die von der Stärke des einfallenden Lichts und von der Oberfläche des bleuchtetenden Körpers abhängen.

Die wichtigste der Beleuchtungs­berechnungen ist die Streureflexion. Diese entsteht durch eine gleichmäßige Reflexion von Licht an kleinsten Partikeln und Inhomo­genitäten der Objekt­oberflächen. Das mathematischen Modell berechnet diesen Sachverhalt mit dem Lambertschen Kosinussatz:

Die Intensität des reflektierten Lichts an einer Stelle ist durch die Oberflächen­normale dieses Punkts und der Einfalls­richtung des einfallenden Lichts bestimmt.

Die Einfalls­richtung des Lichts erhalten Sie durch die vektorielle Substraktion der Lichtquellen­position und des Schnittpunkts. Wenn Sie diesen Vektor normalisieren, berechnen Sie die Intensität der Streureflexion mit Ls = n⃗ * r⃗ r⃗ stellt die Normale und r⃗ die Einfalls­richtung dar.

Weiterhin berück­sichtigen Sie die sogenannte spiegelnde Reflexion. Sie entsteht dadurch, daß sich die Lichtquellen selbst, die in der Realität eine endliche Ausdehnung besitzen, auf der Kugel­oberfläche spiegeln. Sie können die spiegelnde Reflexion, auch Glanzlichter genannt, zum Beispiel als helle Punkte auf Billardkugeln beobachten. Jeder Arbeitschritt schafft realistischere Welten im drei­dimensionalen Raum.

Da Sie keine Lichtquellen endlicher Ausdehnung vorliegen haben, erschaffen Sie dieses Phänomen anderweitig. Hierzu spiegeln Sie den Lichtstrahl des einfallenden Lichts an der Oberfläche der Körper: Sie berechnen den Kosinus des Winkels zwischen dem gespiegelten Vektor und dem, den Sie gerade verfolgt haben und mit dem Sie auch den gerade zu behandelnden Schnittpunkt berechnet haben. Sind dieser Kosinus – und somit auch der Winkel – in einer gewissen Toleranz wie zum Beispiel +-10 Grad, dann haben Sie an dieser Stelle ein Glanzlicht.

Die Intensität errechnen Sie, indem Sie den Kosinus mit einer relativ großen ganzen Zahl potenzieren. Meistens liegen diese Zahlen im Bereich von 10 bis 100 . Die Farbe des Glanzlichts ist, da es sich um das Spiegelbild der Lichtquelle handelt, unabhängig von der Farbe des Körpers. Die Berechnung der Glanzlichter weicht von der physikalischen Realität ab, liefert aber trotzdem realistische Ergebnisse.

Reflexion und Lichtbrechung

Wenn ein Lichtstrahl den Körper anschneidet und Licht dabei reflektiert, spiegeln Sie den Lichtstrahl an seiner Oberfläche und berechnen für die resultierende Halbgerade die Farbe rekursiv.

Die Spiegelung eines Richtungs­vektors an einer Oberfläche erhalten Sie mit relativ einfachen Mitteln: Wenn e⃗ der einfallende Strahl ist, n⃗ die Oberflächen­normale, so gilt für den reflektierten Strahl r⃗ = e⃗ / (e⃗ * n⃗) + 2 * n⃗

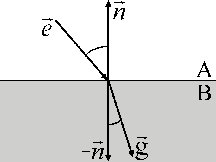
Bei der Transmission, der Lichtbrechung, ist außer dem Anteil des Lichts, das durch das Material dringen kann, noch das Verhältnis der sogenannten Brechzahlen von Interesse. Die Brechzahl ist ein Maß, wie stark Licht abgelenkt werden kann. Wasser hat zum Beispiel eine höhere Brechzahl als Luft.

Dringt ein Strahl von einem Medium A in das Medium B ein

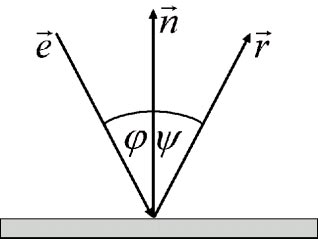
berechnet sich die Richtung des gebrochenen Strahls wie folgt:

b = Brechzahl Medium A / Brechzahl Medium B
s = - e⃗ * n⃗
		

Ist der Term (1 - b² * (1 - s²)) kleiner Null, tritt der Fall der sogenannten Totalreflexion auf. In diesem Fall existiert kein gebrochener Strahl, sondern das Licht wird an der Oberfläche reflektiert und der Strahl auch dement­sprechend behandelt. Dieses Phänomen ist zum Beispiel an den Rändern von Luftblasen unter Wasser zu beobachten.

Ist dieser Term aber größer oder gleich Null, dann berechnen Sie den resultierenden Vektor mit

g⃗ = b * e⃗ + (b * s - sqrt(1 - b2 * (1 - s2))) * n⃗
		

Die Beleuchtungs­gleichung

Diese Erkenntnisse lassen sich in einer großen, auf den ersten Blick schwer überschaubaren Gleichung zusammenfassen. Beim zweiten Hinsehen wird aber schnell klar, woher die Terme stammen: Für die Intensität I eines Farbkanals, die es hier in Rot, Grün und Blau gibt, gilt jeweils: I = Ia * Ka * Of + Für jede beleuchtende Lichtquelle gilt:

[-Kd * Of * (n⃗ * l⃗) + Ks *
((h⃗ * l⃗) ^ p] + Kr * Ir + Kt * It
		

Ia, Ir und It kennzeichnen die Intensitäten des ambienten Lichts und der reflektierten bzw. trans­mittierten Strahlen. Die Koeffizienten Kd, Ks, Kr und Kt (sprich der Prozentsatz) bestimmen Streureflexion, Glanzlichter, Reflexion und Transmission.

l⃗ bezeichnet den Strahl vom Schnittpunkt zur Lichtquelle und h⃗ den gespiegelten Vektor des zu verfolgenden Strahls. Of gibt als Teil der Material­eigenschaften eines Körpers an, wieviel Licht des entsprechenden Kanals absorbiert wird. Prinzipiell müßten Sie für jeden Farbkanal im RGB-Farbsystem, mit dem Sie arbeiten wollen, diese Gleichung lösen. Das ist aber kein Problem, da die Koeffizienten alle gleich sind.

Im Sourcecode des Raytracers erkennen Sie genau die einzelnen Terme der Beleuchtungs­gleichung. Den Teil Für jede beleuchtende Lichtquelle finden Sie als for-Schleife und Schattentest zusammen mit den weiteren Implemen­tationen in

void RTCamera :: RecursiveRaytracing(...)
		

Die Implementation

Bei der Implementation eines Raytracers, den Sie in den nächsten zwei Ausgaben noch erweitern werden, planen Sie genau, wie die Code-Teile zusammenhängen und wirken sollen. Es bietet sich auf jeden Fall eine objekt­orientierte Variante an, da Sie Vererbungs­hierarchien bei Primitiven nutzen, denen Sie später noch neue hinzufügen. Damit bleibt die Gliederung über­sichtlicher.

Als Grundbaustein nutzen Sie die Objekt­basisklasse RTObject: mit Methoden, um Material­information zu setzen, Transforma­tionen anzuwenden und Schnittpunkte zu erfragen. RTPlane ist die Ebenenklasse, die die Methoden für das Primitiv implementiert. RTSphere implementiert die Klasse des Kugelprimitivs.

Eine zweite Objekt­hierarchie stellen die Lichtquellen dar, von denen es zwar bisher nur eine Klasse gibt, aber weitere geplant sind: RTLightSource mit Methoden für die Transformations­anwendung und den Schattentest. RTPointLight implementiert die punktförmigen Lichtquellen.

Zusätzlich nutzen Sie die Kameraklasse RTCamera mit kamera­spezifischen Operationen und der rekursiven Raytracing-Prozedur.

Die letzte Klasse RTScene umfaßt die mathematische Welt mit ihren Informationen wie Kamera, Objekte und Lichtquellen.

Mathematische Welten

Im letzten Teil legen Sie eigene 3D-Welten an. Denkbar ist zum Beispiel, Objekte fest im Programmcode zu verankern, was aber schwierig ist. Darum verwenden Sie am besten eine Skriptsprache wie eine eigene Programmier­syntax, die auf die Beschreibung von Raytracing-Szenen zugeschnitten ist.

Dazu benötigen Sie einen Programmteil, der diese Skriptsprache interpretiert und die Objekte erzeugt. Diesen Teil finden Sie im Sourcecode in der Datei parser.cpp.

Szenen­beschreibungen in diese Skriptsprache bilden Blöcke mit einem Block­bezeichner und Daten. Manche dieser Blöcke sind Bestandteil anderer Blöcke. Kommentare in Blöcken begrenzen Sie wie in C durch /* und */ oder bringen sie in // -Zeilen unter. Vektoren geben Sie in eckigen Klammern an wie <x1, x2, x3>, Zahlen ohne Klammern. Der erste Block definiert die Kameraoptionen:

camera
	{position <5.0,-20.0,18.0>
look_at < 0.0,0.0,0.0> //K.ziel
up < 0,0,-1> //Kamera oben?
fov 25.0 //Öffnungswinkel
aspectratio 1.333333
//Breite/Höhe des Bildschirms }
		

Lichtquellen definiert diese mathematische Welt im Block

light
	{
	position <-5.0,0.0,10.0> //Ort
	color < 0.5,0.5,0.5> //L.Farbe
	}
		

Ein weiterer Block ist das Material. Die Skriptsprache kennt zuerst das defaultmaterial. Dieses definieren Sie an einer beliebigen Stelle im Skript und weisen es jedem neuen Primitiv zu, wenn Sie dafür keine expliziten Material­informationen angeben.

Die einzelnen Parameter eines Materialblocks sind:

defaultmaterial
{
rgb < 0.5, 0.5, 0.5> //RGB-Farbe
reflection 0.5 // Reflexkoef.
refraction 0.0 // Transparenz
diffuse 0.5 // Reflex.Koeffiz.
ambient 0.0 // Reflex.Koeffiz.
specular 1.0 // Koeffiz.für
// spiegelnde Reflexion
pow 50.0 // Potenz dafür
ior 1.0 // Brechzahl-Material
}
		

Ein Kugelprimitiv erzeugen Sie mit folgenden Zeilen:

sphere
{ < x1,x2,x3>, Radius (Zahl) }
		

Wollen Sie für ein Primitiv nicht das defaultmaterial verwenden, fügen Sie einen eigenen Materialblock ein:

sphere
{ < x1,x2,x3>, Radius (Zahl)
	material
	{ ... // Daten wie oben }
}
		

Eine Ebene erzeugen Sie mit folgendem Block, wobei die drei Vektoren die Antragspunkte sind:

plane
{	< 0.0, 0.0, 0.0 >,
	< 1.0, 0.0, 0.0 >,
	< 0.0, 1.0, 0.0 > }
		

Weitere Blöcke, die Sie einem Primitiv noch zuordnen können, enthalten Angaben über zusätzliche Transforma­tionen. So können Sie ein Primitiv nachträglich skalieren, drehen oder verschieben. Die Befehle, die Sie wie das material in den Primitivblock einbauen, lauten:

rotate < Vektor> // Drehung
translate < Vektor> //Schiebung
scale float // Skalierung
		

Mit dieser Skriptsprache können Sie experi­mentieren. Alle Bilder für diesen Artikel berechnen Sie mit dem Raytracing­programm. Skriptdateien dazu finden Sie in den Sourcecodes.

Wenn Sie den Raytracer starten, kann es Stunden dauern, bis das Programm komplexe mathematische Welten berechnet und am Bildschirm dargestellt hat. Diese Arbeit wollen Sie nicht dadurch verwerfen, daß das Programm zu Ihrem Desktop schaltet.

Deshalb haben wir das Basissystem, aufbauend auf vorhergehenden Ausgaben von PC Underground, um eine bmp-Speicher-Routine erweitert. Lassen Sie sich überraschen, welche weiteren Features die beiden folgenden Ausgaben vorstellen werden.