Mit Kegel und Zylinder

Carsten Dachsbacher/Nils Pipenbrinck

Mit den Erweiterungen in diesem zweiten Teil unserer Raytracer-Serie zaubern Sie weitaus realistischere Landschaften auf Ihren Bildschirm. Doch bevor Sie die vielen Neuerungen in Ihren Raytracer einbauen und sehen, machen Sie sich an die mathematische Herleitung der Zylinder- und Kegelprimitive. Mit mathematischer Kleinarbeit verfolgen Sie die Lichtstrahlen und ihre verschieden­artigen Spiegelungen.

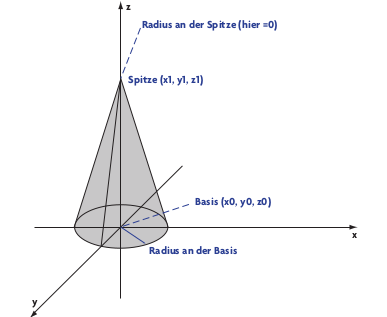
Als erstes untersuchen Sie einen Kegel, wie ihn der Sourcecode zum Raytracing-Artikel (Heft 10, ab S. 226, auch auf der aktuellen Heft-CD) vorweggenommen hat. Es handelt sich hierbei um einen Spezialfall eines Kegels, bei dem die Basis, also der Mittelpunkt der unteren Kreisfläche, im Ursprung des Koordinaten­systems liegt, und die Spitze sich auf der positiven z-Achse befindet. Sie können die Schnittpunkt­berechnungen aller Kegel auf Schnittpunkte mit solch einem Kegel zurückführen. Und so berechnen Sie diesen Kegel:

Wie bisher beschreiben Sie den verfolgten Lichtstrahl durch eine Halbgerade, hier gegeben durch ihren Startpunkt g⃗ und ihren Richtungs­vektor ∂ g⃗, wobei t > 0 gilt: x⃗ = g⃗+ t* ∂ g⃗ Stellen Sie sich nun den Kegel als einen Stapel von Kreisscheiben vor, deren Radius von der Höhe abhängt (Ihrer z-Koordinate), in der Sie liegen. So hätte die unterste Kreisscheibe den Radius des Basiskreises und die oberste den Radius 0.

Da sich der Radius linear ändert, stellen Sie eine Formel auf, die den Radius abhängig von z beschreibt. In dieser Formel lassen Sie für die Spitze auch ein Radius ungleich Null zu, was einen Kegelstumpf beschreiben würde:

Radius(z) = Radius(Basis) + (Radius(Spitze) - Radius(Basis)) * z / z1
		

oder: Radius(z) = Radius(0) + dr * z mit dr = (Radius(z1) - Radius(z0)) / z1 Den Schnittpunkt mit einer Kreisscheibe bestimmen Sie – fast analog zur Berechnung der Schnittpunkte mit Kugeln – über die Abstands­berechnung. Auf einem Kreis liegen alle Punkte x->, deren Abstand vom Mittelpunkt gleich dem Radius des Kreises ist, also: |m⃗ - x⃗| = d⃗ = radius Da Sie sich bei einem Kreis im Zwei­dimensionalen befinden, sind nur die x und y-Komponenten von m⃗, x⃗ und d⃗ von Interesse:

d⃗ * d⃗ = radius2
d⃗x * d⃗x + d⃗y * d⃗y = radius2
		

Bei unserem Kegel ist der Radius jedoch nicht fest, sondern abhängig von z. Daraus ergibt sich:

d⃗x * d⃗x + d⃗y * d⃗y = Radius(z)2
d⃗x * d⃗x + d⃗y * d⃗y = (Radius(0) + dr * x⃗z)2
(m⃗x - x⃗x) * (m⃗x - x⃗x) + (m⃗y - x⃗y) * (m⃗y - x⃗y) = (Radius(0) + dr * x⃗z)2
		

Nun ersetzen Sie wieder alle x⃗ durch die Gleichung der Halbgeraden:

(m⃗x - (g⃗x + t * dg⃗x)) * (m⃗x -(g⃗x + t * dg⃗x)) +
	(m⃗y - (g⃗y + t * dg⃗y)) * (m⃗y - (g⃗y + t * dg⃗y)) =
	(Radius(0) + dr * (g⃗z + t * dg⃗z))2
		

Durch Ausmulti­plizieren erhalten Sie dann:

(m⃗x - g⃗x)2 - 2 * (m⃗x - g⃗x) * t * dg⃗x + t2 *
	(dg⃗x)2 + (m⃗y - g⃗y)2 -
	2 * (m⃗y - g⃗y) * t * dg⃗y + t2 * (dg⃗y)2 =
	(Radius(0) + dr * g⃗z)2 + t2 *
	(dr * dg⃗z)2 + 2 * t *
	(dr * dg⃗z) * (Radius(0) + dr * g⃗z)
		

Nun fassen Sie alle Terme so zusammen, damit Sie wieder eine quadratische Gleichung erhalten – wie bei der Schnittpunkt­berechnung mit Kugeln: a * t² + b * t + c = 0 mit

a = (dg⃗x)2 + (dg⃗y)2 - (dr * dg⃗z)2 - (dr * dg⃗z)2
b = -2 * (m⃗x - g⃗x) * dg⃗x - 2 * (m⃗y - g⃗y) * dg⃗y -
	2 * (dr * dg⃗z) * (Radius(0) + dr * g⃗z)
c = (m⃗x - g⃗x)2 + (m⃗y - g⃗y)2 -
	(Radius(0) + dr * g⃗z)2
		

a, b und c sind reelle Zahlen. Die möglichen Lösungen sind:

t1 = (-b + sqrt(b2 - 4 * a * c)) / (2 * a);
t2 = (-b - sqrt(b2 - 4 * a * c)) / (2 * a);
		

Die Zahl der Lösungen läßt sich durch die Diskriminante D = b² - 4 * a * c bestimmen: Für D < 0 gibt es keine Lösung, D = 0 bringt eine Lösung, und D > 0 führt zu zwei Lösungen.

Setzen Sie t1 und t2 in die Halbgeraden­gleichung ein. Denken Sie daran, nur die Position t1 und t2 sind interessant. Sie erhalten dann die Schnittpunkte.

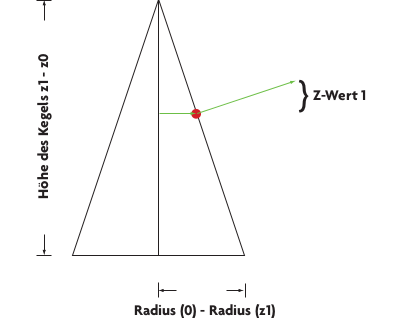
Die Berechnung der Oberflächen­normalen gestaltet sich komplizierter als bei einer Kugel. Hier berechnen Sie zuerst den Differenz­vektor des Schnittpunkts (rot eingezeichnet) mit dem Punkt auf der Mittelachse des Kegels, der auf gleicher Höhe liegt, d.h. den gleichen z-Wert besitzt: d⃗ = s⃗ - (0, 0, s⃗z) Normalisieren Sie diesen Vektor, und skalieren Sie ihn mit folgendem Term:

Skalierungsfaktor = (z1 - z0) / (Radius(0) - Radius(z1))
		

Der Skalierungs­faktor beschreibt, wie steil der Kegelmantel ist, also das Verhältnis seiner Höhe zu seiner Breite.

Da eine Normale immer senkrecht zu einer Oberfläche steht, muß die Normale des Kegels flacher sein, wenn der Kegel steiler wird. Das erreichen Sie, indem Sie den Vektor skalieren und die z-Komponente des resultierenden Vektors, die an dieser Stelle der Berechnung immer 0 ist, auf 1 setzen.

d⃗ = d⃗ * Skalierungsfaktor
d⃗z = 1
		

Der resultierende Vektor d⃗ ist die gesuchte Normale.

Am besten ist, Sie versuchen sich die Berechnung der Normalen anhand kleiner Skizzen verschiedener Kegel vorzustellen. Dabei bleibt die Frage, wie Sie alle möglichen Kegel auf den hier hergeleiteten Spezialfall zurückführen. Die Antwort liefert die Matrizen­rechnung.

Dazu berechnen Sie eine Matrix, die die Transformation einer anderen Matrix rückgängig macht. Mathematiker bezeichnen dies als eine inverse Matrix.

In PC Underground, Heft 10/99, wurden alle Transformationen eines Objekts und die durch die Kamera resultierenden Transformationen in einer Matrix eines jeden Objekts zusammengefaßt (ab S. 212). Diese Matrix benutzen Sie, um zum Beispiel Koordinaten eines Objekts in den Raum der Kamera zu transformieren.

Umgekehrt können Sie eine Matrix zu einem Kegel konstruieren, die einen Punkt im Raum so abbildet, daß Sie den Spezialfall erhalten. Multiplizieren Sie zum Beispiel die Kegelspitze, die Sie frei im Raum plazieren können, mit dieser Matrix, erhalten Sie einen Punkt auf der positiven z-Achse; transformieren Sie die Basis des Kegels, erhalten Sie den Ursprung. Man spricht hierbei von einem Wechsel des Koordinaten­systems.

Der große Vorteil von Matrizen ist, daß Sie solche Matrizen invertieren können. Sie berechnen also eine Matrix, die genau die umgekehrte Abbildung zur Folge hat. Haben Sie also einen Schnittpunkt im Koordinaten­system des Kegels – wie zuvor beschrieben – berechnet, können Sie ihn mit der invertierten Matrix in seine richtige Position im Raum zurücktrans­formieren.

Ohne Sie mit den Details der Matrixrechnung zu belasten, lernen Sie hier die Lösungsidee für das Aufstellen der Kegelmatrix kennen.

Die Matrix für die Abbildung in das gewünschte Koordinaten­system des Kegels erhalten Sie, indem Sie drei senkrecht aufeinander stehende Vektoren finden, bei denen im Kreuzungspunkt der Basismittel­punkt des Kegels und dessen Spitze auf der z-Achse liegt. Den ersten Vektor erhalten Sie durch Subtraktion des Ortsvektors der Spitze vom Ortsvektor des Basismittel­punkts.

Nun benötigen Sie einen Vektor, der senkrecht zu diesen steht. Eine einfache Methode besteht darin, zwei Komponenten des ersten Vektors zu vertauschen und eine der vertauschten zu negieren. Den dritten Vektor, der senkrecht auf den ersten beiden steht, erhalten Sie durch das Kreuzprodukt dieser Vektoren.

Damit haben Sie eine Matrix, die den Kegel so rotiert, daß er die richtige Orientierung für den Spezialfall besitzt. Jetzt fehlt noch eine Verschiebungs­matrix zur Lösung. Diese verschiebt alle Punkte um das Negative des Ortsvektors des Basismittel­punkts. Die Matrix für den Kegel erhalten Sie also aus der Matrixmulti­plikation (Hintereinander­ausführung) der Verschiebungs- und Rotations­matrix.

Mit der Berechnung von Schnittpunkten mit Kegeln haben Sie den allgemeineren Fall kennengelernt. Ein Spezialfall des Kegels ist der Zylinder. Bei einem Zylinder ist der Radius unabhängig von der z-Komponente, das heißt die Formeln für die Schnittpunkt­berechnung vereinfachen sich deutlich. Sie finden das Resultat im Sourcecode. Eine weitere Herleitung ergibt keinerlei Neuerung gegenüber dem Kegel.

Die Implementation des Kegel- und Zylinder­primitivs finden Sie in im Quellcode von RTCone.cpp und RTCylinder.cpp.

Licht aus endlichen Quellen

In PC Magazin 10/99 haben Sie ab S. 212 den einfachsten Fall von Lichtquellen beim Raytracing kennengelernt. Dabei handelte es sich um Lichtquellen, die von einem Punkt aus Licht in alle Richtungen aussenden, ohne selbst eine licht­emittierende Fläche zu besitzen.

Doch diese Vorstellung entspricht nicht den real vorhandenen Lichtquellen. Der deutlichste Unterschied, den punktförmige und sich ausdehnende Lichtquellen besitzen, ist, daß punktförmige immer einen harten Schatten werfen, während Sie in der Realität fast immer weiche Schatten vorfinden.

Wie Sie eine solche Lichtquelle in einen Raytracer implementieren, zeigt Ihnen dieser Teil. Dabei ändern Sie die rekursive Raytracing-Prozedur nur an zwei Stellen.

Die erste Stelle ist die Schatten­berechnung. Es genügt nun nicht mehr, einen Schattenstrahl auszusenden, sondern Sie benötigen mehrere – besser gesagt viele.

Bei einem Schattentest prüfen Sie die Sichtbarkeit der Lichtquelle mit verschiedenen, möglichst gleichmäßig auf der Lichtquelle verteilten Punkten. Der Schattentest eines einzelnen Punkts funktioniert genauso wie bei punktförmigen Lichtquellen. Die resultierende Farbe ergibt sich durch Mittelung der Schattenfarben aller Schatten­strahlen.

Im Pseudocode sieht die Vorgehensweise wie folgt aus:

for (viele Schattenstrahlen)
{
	Wähle Punkt auf der Lichtquelle
	Berechne Schattenfarbe für diesen Punkt per Schattentest
	Kumuliere Schattenfarbe
}

Resultierende Schattenfarbe = Kumulierte Schattenfarbe / Anzahl Schattenstrahlen
		

Die Auswahl der Zielpunkte auf der Lichtquelle erledigen Sie mit einem Zufalls­generator, wobei die Punkte möglichst gut verteilt liegen sollten. Das erreichen Sie, indem Sie jeden bereits berechneten Punkt speichern.

Benötigen Sie dann einen neuen Zufallspunkt, generieren Sie mit einem Zufallszahlen­generator mehrere neue Kandidaten, nehmen aber nur denjenigen, der von allen Zufallspunkten den größten Abstand besitzt. Je mehr Kandidaten Sie zulassen, desto besser wird die zufällige Verteilung.

Da Sie aber nur im Halbschatten viele Schatten­strahlen benötigen, um ein gutes visuelles Ergebnis zu erhalten, definieren Sie ein Abbruch­kriterium. Dieses stellt sicher, daß weitere Schatten­strahlen getestet werden, wenn die Helligkeit der bisherigen zu stark variiert. Umgekehrt lassen Sie zu, daß der Schattentest endet, wenn die Schatten­strahlen alle ähnliche Helligkeit besitzen.

Aus diesen Überlegungen ergibt sich als mögliche Formel:

max = Max. aller Helligkeiten
min = Min. aller Helligkeiten
if((max - min) / (max + min) > Toleranzschwelle) mehr Strahlen;
else Ende;
		

Die Funktionen dazu, die von den Schattenfarben auch die Rot-, Grün- und Blau­komponenten separat behandeln, finden Sie in der Datei RTFunctions.h. Zusätzlich zu diesem Abbruch­kriterium legen Sie noch eine mindeste und eine maximale Anzahl von Schatten­strahlen fest.

Bedenken Sie, daß eine gute Darstellung von solchen Lichtquellen gewaltigen Rechenaufwand erfordern kann. Die Werte für die minimale Zahl von Schatten­strahlen liegen zwischen 4 und 8, die der maximalen Zahl bei 100 oder mehr.

Der zweite Punkt, an dem Sie in der Raytracing-Prozedur Hand anlegen, ist die Berechnung der Glanzlichter. Bei punktförmigen Lichtquellen haben Sie das einfallende Licht an der Oberfläche eines Körpers gespiegelt. Die Intensität des Glanzlichts hing dann davon ab, wie genau der Betrachter von diesem gespiegelten Strahl getroffen wurde.

Nun gehen Sie den umgekehrten Weg. Sie spiegeln den einfallenden Lichtstrahl und testen, ob dieser Lichtstrahl einen Schnittpunkt mit der Lichtquelle besitzt. Wenn ja, ist die Intensität des Glanzlichts maximal und seine Farbe die der Lichtquelle. Gibt es keinen Schnittpunkt, existiert für den betrachteten Oberflächen­punkt kein Glanzlicht.

An dieser Stelle ist interessant, welche Form die neue Lichtquelle besitzt. Als Beispiel für diesen Raytracer haben wir eine rechteckige Lichtquelle verwendet. Die Schnittpunkt­berechnung, die Sie für die Glanzlichter verwenden, heißt BOOL IntersectTriangle(...) und befindet sich in RTFunctions.h. Eine entsprechende Herleitung nimmt die nächste Ausgabe in Angriff, die auch polygonale Primitive und aus Polygonen zusammen­gesetzte Objekte behandelt.

Texturen & Bumpmapping

Nachdem Sie sich mit einer Reihe von geometrischen Primitiven beschäftigt und auch einiges an Aufwand mit den Lichtquellen getrieben haben, widmen Sie sich nun den Oberflächen der Objekte. Bisher haben Sie Oberflächen durch ihre physikalischen Parameter, wie den Reflektions­koeffizienten oder die Transparenz, und durch ihre Eigenfarbe definiert.

Damit konnten Sie nur die Eigenschaften für die ganze Oberfläche bestimmen. Viel interessanter gestaltet sich eine Szene, wenn Sie die Objekte mit Texturen belegen oder ihren Oberflächen eine aufgerauhte Struktur oder Beulen verpassen.

Prinzipiell können Sie Objekte mit zwei Arten von Texturen belegen:
• Das eine Verfahren projeziert eine zwei­dimensionale Bitmap auf einen Körper. So arbeiten 3D-Beschleuniger sowie die auf Polygonen basierenden 3D-Engines.
• Bei Raytracern verwenden Sie hingegen fast immer sogenannte prozedurale Texturen. Hierbei setzen Sie keine Bitmaps ein, sondern berechnen die Farbe von Punkten im Raum.

Im Zusammenhang mit prozeduralen Texturen und Raytracern fällt immer der Begriff Perlin Noise. Dieses Verfahren, das Ken Perlin entwickelt hat, setzen Experten häufig ein, um Texturen zu synthetisieren. Besuchen Sie Ken Perlin auf seiner Homepage: mrl.nyu.edu/perlin

Perlin Noise

Wenn Sie sich Dinge in der Natur ansehen, stellen Sie fest, daß es verschiedene Detailstufen gibt, ähnlich wie bei Fraktalen. Ein anschauliches Beispiel ist ein Gebirge. Es enthält große Höhen­unterschiede wie Berge, mittlere wie Hügel, kleine wie Felsbrocken und winzige Details wie Steine.

Noise bedeutet so viel wie Lärm oder Rauschen. Eine Noise-Funktion ist eine Funktion, die zu einem Parameter – in diesem Fall eine ganze Zahl – eine zufällige Zahl zurückliefert. Wenn Sie zweimal denselben Parameter übergeben, muß sie auch zweimal dasselbe Resultat erzeugen, sonst funktioniert das Perlin-Noise-Verfahren nicht.

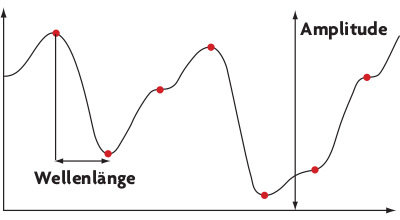
Perlin Noise ahmt die in der Natur vorkommenden Detailstufen nach, indem es unterschied­lich skalierte Noise-Funktionen nach einem System addiert. Beachten Sie bei der im Bild unten dargestellten Noise-Funktion, daß nur die roten Punkte generierte Zufallszahlen sind. Alle Zwischenwerte sind durch Interpolation entstanden. Die Wellenlänge bezeichnet den Abstand zweier Zufallszahlen. Die Frequenz berechnet sich – analog zu Wellen in der Physik – als Kehrwert der Wellenlänge.

Addieren Sie mehrere Noise-Funktionen, wie im Bild unten zu sehen, erhalten Sie die Perlin-Noise-Funktion. Dasgleiche können Sie auch im zwei­dimensionalen Raum tun. Dazu benötigen Sie nur eine Noise-Funktion, die zu einem Zahlenpaar einen Zufallswert liefert. Das Ergebnis sehen Sie im Bild, das schattierte Grünflächen zeigt.

Die Amplitude und die Frequenz, die Sie für die einzelnen Noise-Funktionen verwenden, legen Sie durch die sogenannte Persistence fest. Sie bestimmen noch eine Amplitude und eine Frequenz für die erste Funktion. Für die jeweils nächste Funktion verdoppeln Sie die Frequenz und multiplizieren die Amplitude mit der Persistence.

Der Wert der Persistence sollte zwischen 0 und 1 liegen. Größere Werte bedeuten stärkere hohe Frequenzen, also mehr Rauschen. Bei der Anzahl der Funktionen, die überlagert werden, spricht man auch von Oktaven. Der Begriff wurde aus der Musik entliehen, da bei Klängen eine Verdopplung der Frequenz einem Sprung von einer Oktave entspricht.

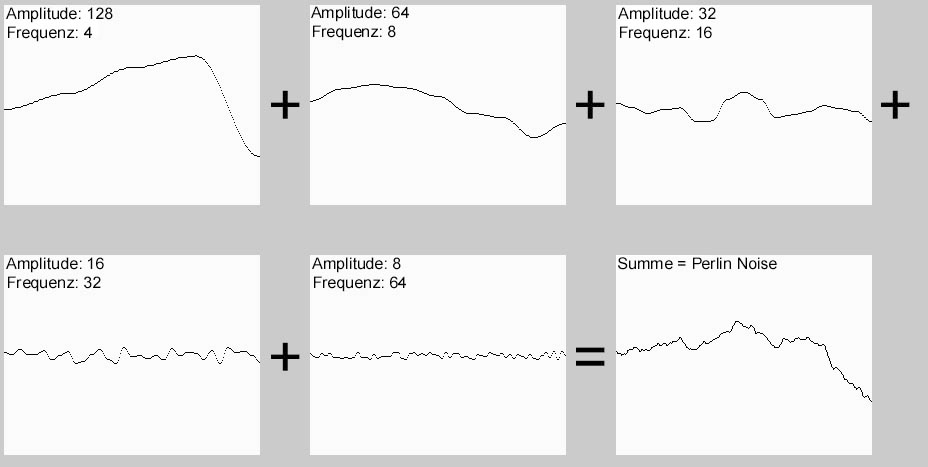
Wieviel Oktaven Sie wählen, ist Ihre Entscheidung. Berück­sichtigen Sie nur, daß die Amplitude irgendwann so klein wird, daß die Funktion nicht mehr ins Gewicht fällt. In unserem Fall empfehlen sich etwa zwei bis acht Oktaven.

Wie erzeugen Sie Noise-Funktionen? Die herkömmlichen Zufallszahlen­generatoren, die Ihnen in C zur Verfügung stehen, liefern bei jedem Aufruf eine neue Zahl. Da das Ergebnis jedoch reproduzierbar sein muß, weil Sie eine Noise-Funktion eventuell mehrmals an derselben Stelle berechnen müssen, können Sie diese nicht verwenden.

Eine Möglichkeit besteht darin, eine Funktion zu finden, die relativ zufällig Werte liefert. Solche Funktionen enthalten meist sehr große Primzahlen. Ein Beispiel mit Zufallszahl zwischen -1 und 1 zu x sieht so aus:

x = (x < 13) ^ x;
return (1.0 - ((x * (x * x * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0);
		

Ein anderer Lösungsweg: Legen Sie beim Start des Programms eine Tabelle mit Zufallszahlen mit Hilfe Ihres herkömmlichen Generators an. Es genügen 4096 verschiedene Zahlen. Als Funktion dient dann

return Zufallstabelle[x % Größe der Tabelle ];
		

Wenn Sie nun einen Zufallswert zu nicht ganzzahligen x-Werten benötigen, erledigen Sie dies durch Interpolation.

Dazu werten Sie die Noise-Funktion an der von x aus gesehen nächst­kleineren und nächstgrößeren ganzen Zahl aus. Mit dem Nachkomma­anteil von x berechnen Sie den interpolierten Wert. Die einfachste Methode ist es, linear zu interpolieren:

return Wert1 * (1 - NachkommaX) + Wert1 * NachkommaX
		

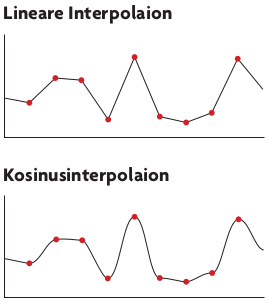
Bei der linearen Interpolation erhalten Sie jedoch keine sehr schönen Ergebnisse. Mit ein wenig mehr Rechenaufwand erzielen Sie mit der Kosinus­interpolation abgerundetere Ergebnisse:

ft = NachkommaX * PI
f = (1 - cos(ft)) * 0.5
return a * (1 - f) + b * f
		

Der Unterschied ist, daß der Gewichtungs­faktor (hier f ) bei der Kosinus­interpolation – durch die Kosinus­funktion an den Rändern (sprich bei Nachkomma­anteilen nahe bei 0 oder 1 – langsamer steigt. Dadurch erhalten Sie in der Nähe der Zufallswerte abgerundete Verläufe.

Nehmen Sie nun alles zusammen, erhalten Sie eine Perlin-Noise-Routine wie im folgenden Pseudocode für eine Dimension:

int Noise(int x)
{
		return Zufallstabelle[x % Größe der Tabelle];
}

float Interpolate(float a, float b, float x)
{
	return a * (1 - x) + b * x;
}

float InterpolatedNoise(float x)
{
	GanzzahlX = (int)x;
	NachkommaX = x - GanzzahlX;
	v1 = Noise(x);
	v2 = Noise(x + 1);
	return Interpolate(v1,v2,NachkommaX);
}

float PerlinNoise(float x)
{
	floattotal = (float)0;
	floatPersistence = material.p;
	int Octaves = material.o;
	floatFrequenz = material.f;
	floatAmplitude = material.a * Persistence;
	for(int i = 0; i < Octaves; i++)
	{
		total += InterpolatedNoise3D(x * Frequenz) * Amplitude;
		Frequenz *= 2.0;
		Amplitude *= Persistence;
	}
}....

		

Für drei­dimensionale Noise-Funktionen berechnen Sie nicht zwei Punkte und interpolieren, sondern Sie berechnen acht Werte. Ein Punkt liegt im Drei­dimensionalen innerhalb eines Würfels, dessen Kanten durch die jeweiligen nächst­kleineren bzw. -größeren ganzzahligen Koordinaten bestimmt sind. Berechnen Sie die Werte für die Eckpunkte des Würfels, und interpolieren Sie anschließend.

Was haben Sie von einer 3D-Noise-Funktion? Sie können zu jedem Punkt im Raum einen Farb- oder Helligkeits­wert bestimmen. Wollen Sie ein Objekt mit einer prozeduralen Textur versehen, speichern Sie in der Material­struktur des Raytracers die Werte für die Noise-Funktionen und berechnen für jeden Schnittpunkt den Noise-Wert. Damit erzeugen Sie Texturen wie auf den unten abgebildeten Kugeln.

Mit den Noise-Werten berechnen Sie auch andere Texturen, zum Beispiel eine marmorähnliche Struktur. Hierzu berechnen Sie für jeden Raumpunkt zwei Noise-Werte: einen an seiner Original­position und einen an einem Punkt, den Sie durch eine beliebig große Verschiebung erreichen.

Dann nehmen Sie die x-Komponente des Original­vektors und addieren den ersten Noise-Wert dazu. Genauso verfahren Sie mit der y-Komponente und dem zweiten Wert.

Die Nachkomma­stellen der resultierenden Werte bilden Sie mit der Funktion cycloidal( ... ) auf eine Sinusfunktion ab und multiplizieren das Ergebnis mit dem Turbulenz­parameter, den Sie noch in der Material­beschreibung einführen. Der Rückgabewert der Noise-Funktion entspricht jetzt nur der Länge des Ergebnis­vektors, auf eine Dreiecks­funktion umgelegt:

{...}

floatcycloidal(float x)
{
	float temp = fmod(x, 1);
	if(temp < 0) temp += 1;
	return sin(temp * 2 * PI);
}

floattriangle_wave(float x)
{
	float offset = fmod(x, 1);
	if(offset < 0) offset += 1;
	if(offset > 0.5) offset = 1 - offset;
	return offset + offset;
}

{...}

// Marmor Wert am Punkt p
r = Noise(p.x, p.y, p.z);
r2 = Noise(p.x+1000, p.y, p.z);
p.x += cycloidal(p.x + r) * PTexture.Turbulenz;
p.y += cycloidal(p.y + r2) * PTexture.Turbulenz;

return triangle_wave(VLength(p));

{...}
		

Es gibt noch unzählige Wege, um die Noise-Werte zu anderen prozeduralen Texturen zu verknüpfen. Im Sourcecode (RTNoise.cpp) finden Sie eine Variante für holzähnliche Muster.

Wie Sie die Helligkeit der Farbe an einem Schnittpunkt mit prozeduralen Texturen verändern können, so modifizieren Sie auch die Oberflächen­normale an einem Schnittpunkt, um die Beleuchtung, Spiegelung und Lichtbrechung zu beeinflussen. Hierzu berechnen Sie für einen Schnittpunkt drei Noise-Werte, einen an der Original­position und zwei an verschobenen Stellen. Interpretieren Sie diese Werte als Vektor, skalieren Sie ihn, und addieren Sie den Vektor auf die Normale, die Sie im Zuge der Schnittpunkt­berechnungen erhalten haben. Als Ergebnis erhalten Sie die Kugeln rechts im Bild.

Anti-Aliasing

Ein Problem sind die Aliasing-Effekte – auch als Treppenstufen bezeichnet. Als Aliasing wird das irrtümliche Erscheinen von nieder­frequenten Signalen bezeichnet, das aus fehlerhaftem Messen von hochfrequenten Signalen resultiert.

Anders ausgedrückt: Wenn Sie sich den Bildschirm als Fläche vorstellen, repräsentiert jeder Pixel einen kleinen Teil der Gesamtfläche. Verfolgen Sie nur einen Lichtstrahl pro Pixel zurück, können Sie durch zu geringes Abtasten Treppchen­effekte bekommen.

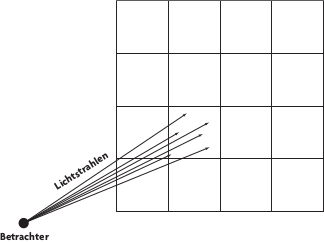
Sie lösen das Problem, indem Sie einen Pixel als Fläche behandeln und mehrere Strahlen durch diesen Pixel verfolgen. Ein Ansatz für das Anti-Aliasing ist das statistische Super-Sampling. Hierbei verfolgen Sie Strahlen, die vom Betrachter aus durch Punkte verlaufen, die zufällig auf der Fläche des Pixels verteilt sind.

Achten Sie dabei darauf, daß diese Punkte, wie schon bei den Schatten­strahlen der Halbschatten, möglichst gleich verteilt sind. Auch die Abbruch­kriterien sind dieselben wie die bereits vorgestellten. Da das Verfolgen der Stahlen der rechen­intensive Teil des Raytracing ist, ist der Preis für das Anti-Aliasing hoch, aber die deutlich bessere Darstellungs­qualität rechtfertigt dies.

Die vorgestellten Neuerungen bei den Texturen und dem Bump Mapping im Raytracing-Programm sind auch in den Parser integriert. Die Parameter für das Abtasten der Lichtquellen und das Anti-Aliasing finden Sie in den Quelldateien RTPolylight.cpp und RTCamera.c.