Primitive in Perfektion

Carsten Dachsbacher/Nils Pipenbrinck

Unsere Welt besteht aus einer Vielzahl von Formen. Daher verlangt die Gestaltung wirklichkeits­getreuer Szenerien in einem Raytracer auch nach komplexeren Objekten. Diese bauen Sie am einfachsten aus Polygonen und sogenannten CSG-Primitiven (Constructed Solid Geometry) zusammen. Dadurch steigt der Anspruch an die Rechen-Performance – dem werden Sie durch gezielte Verbesserungen gerecht.

Polygon-Primitive

An dieser Stelle lernen Sie die Primitive kennen, die Sie wahrscheinlich schon am längsten vermißt haben: Polygone. Wir beschränken uns dabei auf ihre einfachsten Vertreter, die Dreiecke. Für Schnittpunkt­berechnungen mit Dreiecken existieren verschiedener Algorithmen. Wir stellen Ihnen das allgemeine Prinzip vor – eine besonders elegante Variante finden Sie im Quellcode. Sie stammt aus dem Journal of Graphics Tools (siehe Literaturtips am Ende).

Ein Dreieck definieren Sie durch seine drei Eckpunkte. Vielleicht erinnern Sie sich, daß Sie auf die gleiche Weise auch eine Ebene im Raum plaziert haben. Um einen Schnittpunkt mit einem Dreieck zu besitzen, muß eine Gerade notwendiger­weise auch die Ebene schneiden, in der das Dreieck liegt – also die Ebene, die durch die drei Eckpunkte bestimmt wird.

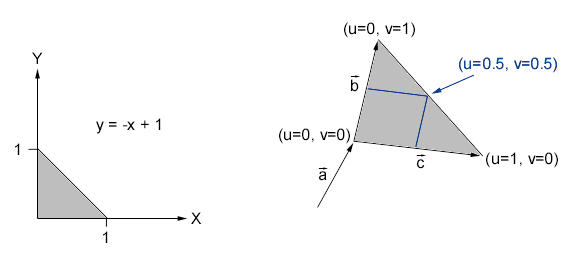
Zudem muß der berechnete Schnittpunkt innerhalb des Dreiecks liegen. Betrachten Sie dazu das Koordinaten­system in der Abbildung unten.

Dort finden Sie die Funktion y = -x + 1 eingezeichnet. Durch Umformen erhalten Sie daraus x + y = 1. Außerdem sehen Sie im Bild ein Dreieck, dessen linker unterer Eckpunkt durch den Ortsvektor a⃗ festgelegt ist und dessen Kanten mit b⃗ bzw. c⃗ beschriftet sind.

Definieren Sie, daß der Einheitsvektor der x-Achse gleich b⃗ und der Einheitsvektor der y-Achse gleich c⃗ ist, können Sie in der obigen Formel x durch u, y durch v und das Gleichheits­zeichen durch „kleiner gleich“ ersetzen. Daraus ergeben sich folgende Bedingungen für die Dreiecksfläche:

u + v <= 1
u >= 0
v >= 0
		

Die Werte u und v für einen berechneten Schnittpunkt s⃗ der Geraden mit der Ebene entnehmen Sie dem Skalarprodukt. Dieses berechnet, wie lang die Projektion eines Vektors auf einen anderen ist. Die Differenz zwischen s⃗ und a⃗ ergibt genau den Vektor, den Sie auf die Kanten des Dreiecks projizieren:

x⃗= s⃗- a⃗
u1 = x⃗ * b⃗
v1 = x⃗ * c⃗
		

Für das Skalarprodukt gilt ganz allgemein:

t * (x⃗* y⃗) = (t * x⃗) * y⃗
		

Um u¹ und v¹ richtig zu skalieren, genügt es daher, sie durch die Länge der Kanten zu teilen:

u = u 1 / |b⃗|
v = v 1 / |c⃗|
		

Daraus ersehen Sie, ob der Schnittpunkt im Dreieck liegt:

if (u > 0 && v>0 && (u + v) <= 1)
	return true;
else
	return false;
		

Nachdem Sie jetzt Schnittpunkte mit Dreiecken berechnen können, bleibt die Frage der Beleuchtung. Natürlich haben Dreiecke eine gerade Oberfläche – genauso wie die Ebenen, in denen sie liegen. Die Normale bleibt also überall dieselbe. Daher bräuchten Sie nur die einmal berechnete Normale in der Beleuchtungs­gleichung verwenden.

Allerdings dienen Dreiecke oft dazu, beliebig geformte Flächen anzunähern. Um zum Beispiel runde Flächen rund erscheinen zu lassen, benötigen Sie eigentlich Unmengen von Dreiecken. Dadurch steigt auch der Rechenaufwand immens. Möchten Sie mit wenigen Dreiecken auskommen, können Sie zumindest in der Beleuchtung die Fläche runder erscheinen lassen, als sie wirklich ist.

Die Phong-Schattierung täuscht gewölbte Flächen durch die Interpolation des Normalen­vektors vor. Dazu weisen Sie nicht jedem Dreieck, sondern jedem Eckpunkt eine Normale zu. Die Normale an einem Schnittpunkt innerhalb des Dreiecks erhalten Sie dann durch die Interpolation der Normalen an den drei Eckpunkten. Zu jedem Dreieck berechnen Sie dazu die Normale an einem der Eckpunkte sowie die Differenzen zu den Normalen an den zwei anliegenden Kanten.

Sind also n⃗₁, n⃗₂ und n⃗₃ die Normalen an den Eckpunkten, dann berechnen Sie:

k⃗= n⃗2 - n⃗1
l⃗= n⃗3 - n⃗1
		

Aus der Schnittpunkt­berechnung besitzen Sie bereits die beiden Parameter u und v. Für die Normale am Schnittpunkt gilt dann:

n⃗ = n⃗1 + u * k⃗ + v * l⃗
		

Bevor Sie diese in die Berechnung der Beleuchtung einsetzen, normalisieren Sie sie noch: Auch wenn die ursprünglichen Normalen an den Eckpunkten bereits normalisiert vorliegen, ist durch die Interpolation nicht mehr gewährleistet, daß n⃗ die Länge 1 besitzt.

In der Skriptsprache des Parsers können Sie sowohl Dreiecke mit konstanter Normale als auch solche mit Phong-Schattierung definieren. Ein 3D-Objekt aus Dreiecken beginnen Sie zunächst mit mesh {...} Innerhalb der geschweiften Klammern geben Sie die zwei Dreiecks­primitive an:

triangle
{
	<x1, y1, z1>, <x2, y2, z2>,
	<x3, y3, z3>
}
		

definiert Dreiecke mit konstanter Normale, die dann berechnet wird. Für Dreiecke mit Phong-Schattierung geben Sie in

smooth_triangle
{
	<x1, y1, z1>, <x2, y2, z2>
	<x3, y3, z3>, <nx1, ny1, nz1>
	<nx2, ny2, nz2>, <nx3, ny3, nz3>
}
		

zusätzlich noch die Normalen der Eckpunkte an.

Ein solches Polygonobjekt sehen Sie im Bild unten. Die Polygondaten dafür stammen aus einer mit POV-Ray generierten Szenerie.

CSG-Primitive

Auch wenn sich durch Polygone prinzipiell alle Oberflächen annähern lassen, ist dies manchmal nicht die einfachste oder genaueste Lösung. Dann eignet sich vielleicht eher die Klasse der durch Constructed Solid Geometry (CSG) erzeugten Körper. Hinter dieser Bezeichnung, die sich nur schwer ins Deutsche übersetzen läßt, verbirgt sich ein Verfahren, mit dem Sie zwei oder mehrere einfache Primitive wie Kugel, Ebene oder Zylinder miteinander verknüpfen.

Die möglichen Verknüpfungen sind dabei Vereinigung, Schnitt und Differenz. Diese Begriffe aus der Mengenlehre können Sie ohne weiteres auf die Primitive übertragen, da diese gewissermaßen Teilmengen des Raums darstellen. Anhand zweier Kugeln können Sie sich die erlaubten Operationen leicht vor Augen führen. Betrachten Sie dazu die rot schraffierte Schnittmenge zweier Kugeln im folgenden Bild.

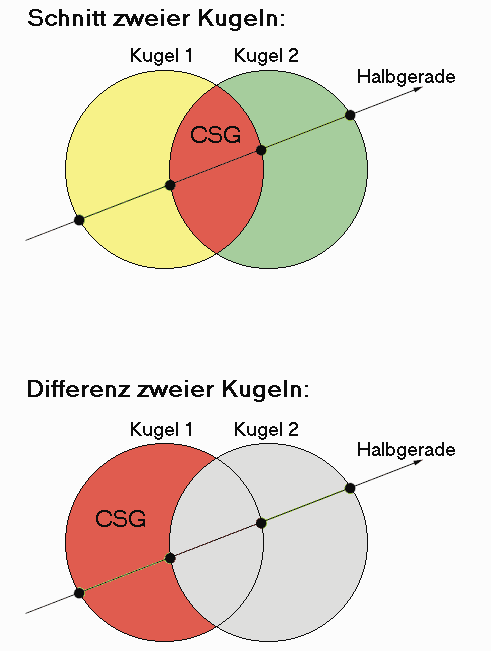
Um die Schnittpunkte mit der Schnittmenge festzustellen, berechnen Sie zunächst alle Schnittpunkte der betrachteten Geraden mit den beiden Primitiven. Die Schnittpunkte mit der Schnittmenge finden Sie durch folgenden Algorithmus in Pseudocode:

Betrachte alle Schnittpunkte der Primitive:
	Ist der Punkt von Primitiv 1 und liegt in Primitiv 2
	oder
	ist der Punkt von Primitiv 2 und liegt in Primitiv 1
dann Schnittpunkt gefunden
		

Sie sehen: Die Primitive – oder vielmehr die entsprechenden C++-Klassen – verlangen eine Methode, die angibt, ob ein Punkt im Inneren des Primitivs liegt. Im Falle der Kugel berechnet diese einfach den Abstand des Punkts vom Kugel­mittelpunkt. Ist er kleiner oder gleich dem Radius, dann liegt der Punkt im Inneren.

Bei einer Ebene ist zunächst unklar, welche Seite den inneren bzw. äußeren Teil darstellen soll. Per Definition sei daher festgelegt, daß der Halbraum – eine Ebene teilt den Raum in zwei Hälften – außen ist, in den die Normale zeigt.

Dadurch reduziert sich der Aufwand für den Innen-/Außen-Test auf ein Skalarprodukt des zu prüfenden Punkts mit der Normalen, wovon Sie noch den (immer vorberechneten) Abstand der Ebene zum Ursprung subtrahieren. Ist das Resultat kleiner oder gleich Null, liegt der Punkt im Inneren.

Natürlich können Sie CSG-Objekte auch aus solchen Primitiven zusammensetzen, die ihrerseits CSG-Objekte sind. Auch diese haben alle für die Schnittpunkt­berechnung notwendigen Methoden implementiert.

Eine weitere mögliche Verknüpfung zweier Objekte ist die Vereinigung. Diese gestaltet sich besonders einfach, da Sie alle Schnittpunkte der Einzel­primitive auch als Schnittpunkte des CSG-Objekts verwenden können. Das ist deshalb erlaubt, da beim Raytracing sowieso der nächste Schnittpunkt gesucht wird. Alle weiter entfernten Schnittpunkte – auch die im Inneren des Vereinigungs­objekts – fallen nicht ins Gewicht.

Die letzte Verknüpfungs­methode ist die Differenz. Sie können sich das als das Heraus­schneiden eines Objekts aus einem anderen vorstellen.

In diesem Fall gilt für die Schnittpunkt­klassifikation:

Betrachte alle Schnittpunkte der Primitive:
	Ist der Punkt von Primitiv 1 und liegt nicht in Primitiv 2
	oder
	ist der Punkt von Primitiv 2 und liegt in Primitiv 1
dann Schnittpunkt gefunden
		

Damit haben Sie das Prinzip der CSG-Objekte erfaßt. Ein Beispiel für ein komplexeres CSG-Objekt ist der Würfel in der Abbildung auf der nächsten Seite. Der Würfel ist die Schnittmenge aus sechs Ebenen. Die Vertiefungen der Augenzahlen entstehen durch heraus­geschnittene Kugeln. Die Skriptdatei dazu finden Sie auf der Heft-CD bei den Quelltexten.

Schnittpunkt­berechnungen optimieren

Wollen Sie die Berechnung eines Bilds mit dem Raytracer beschleunigen, beginnen Sie bei den am häufigsten verwendeten Routinen. Ihr Augenmerk fällt dabei wohl zuerst auf die Schnittpunkt­berechnungen, die den größten Teil der Rechenzeit in Anspruch nehmen. An diesen mathematischen Problemen haben sich bereits viele versucht, und dement­sprechend viele Algorithmen für Schnittpunkt­berechnungen für Primitive aller Art gibt es.

Im Quelltext RTTriangle.cpp des Polygon­primitivs finden Sie etwa einen eleganten Ansatz, um einen Schnittpunkt einer Gerade und eines Dreiecks zu berechnen. An dieser Stelle möchten wir Ihnen zeigen, wie Sie die Schnittpunkte einer Kugel anhand geometrischer Überlegungen schneller berechnen.

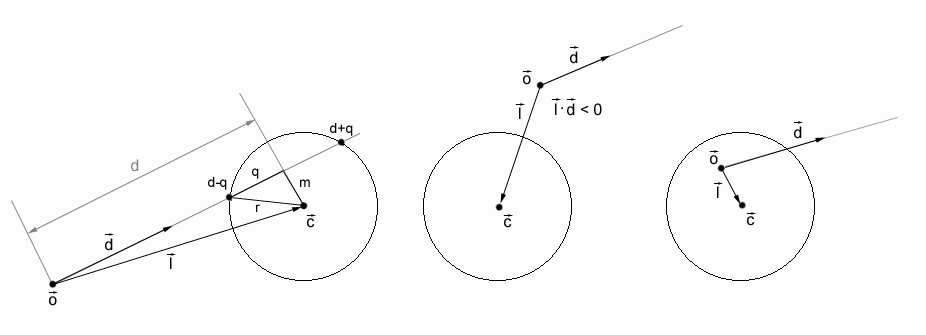
Vor einer Schnittpunkt­berechnung wissen Sie nicht, ob es überhaupt einen Schnittpunkt gibt. Eine oft verwendete Technik bei der Optimierung von Schnittests ist es, durch möglichst einfache Berechnungen bereits sehr früh festzustellen, ob der Strahl das Objekt sicher verfehlt. Diese Tests werden Rejection-Tests genannt – verläuft der Test negativ, gibt es keinen Schnittpunkt. Für den Fall der Kugel betrachten Sie am besten die drei Skizzen unten, die sich jeweils nur in der Lage von o⃗ unterscheiden. o⃗ ist dabei der Startpunkt der Halbgeraden, ∂x⃗ die Richtung der Geraden. Für die Halbgerade gilt:

x⃗ = o⃗ + t * ∂x⃗

Schließlich gibt es noch den Vektor c⃗ für den Kugelmittel­punkt. Der erste Rejection-Test berücksichtigt die Lage der Kugel bezüglich o⃗. Von Interesse sind nur Kugeln, die vor dem Startpunkt der Geraden liegen. Dazu berechnen Sie den Vektor vom Startpunkt zum Kugelmittel­punkt, also

l⃗ = c⃗ - o⃗

Daraus ermitteln Sie die quadrierte Länge von l⃗ – also das Quadrat des Abstandes – mit:

l2 = l⃗ * l⃗

Gleichzeitig haben Sie mit r² das Quadrat des Kugelradius gegeben, der bei der Initialisierung eines Kugelobjekts vorberechnet wird. Damit entscheiden Sie nun folgendes: Ist l² kleiner als r², befindet sich o⃗ in der Kugel, und es gibt (genau) einen Schnittpunkt. Wollen Sie nur feststellen, ob es überhaupt einen Schnittpunkt gibt, können Sie an dieser Stelle die Berechnung abbrechen.

Da Sie allerdings den Schnittpunkt bestimmen wollen, berechnen Sie als nächstes die Projektion von l⃗ auf d⃗. Dies geschieht mit dem Skalarprodukt

d = l⃗ * ∂x⃗

Nun wenden Sie den ersten Rejection-Test an: Liegt o⃗ außerhalb der Kugel – also ist l² größer als r² –, und ist d negativ? Falls ja, gibt es keinen Schnittpunkt. Ansonsten fahren Sie mit der Berechnung fort.

Als nächstes interessiert Sie m², das Abstands­quadrat des Kugelmittel­punkts zu der Projektion von l⃗. Da es sich um ein rechtwinkliges Dreieck handelt, wenden Sie den Satz des Pythagoras an:

m2 = l2 - d2

Nun sind Sie am zweiten Rejection-Test angelangt: Ist m² größer als r², dann wird der Strahl am Objekt vorbeischießen, ansonsten sicher treffen. Im letzteren Fall existieren also Schnittpunkte, die es zu berechnen gilt. Lösen Sie dazu die Gleichung

q2= r2 - m2

Da wegen des letzten Rejection-Tests m² <= r² gilt, ist q² größer oder gleich Null. Das bedeutet, daß Sie ohne Probleme die Wurzel daraus ziehen können:

q = sqrt(q2)

Um schließlich die Schnittpunkte zu bestimmen, berechnen Sie die Entfernungen zu den Schnittpunkten – also die Werte für t aus der Geraden­gleichung. Dabei gilt:

t1 = d - q
t = d + q
		

Die Routine sieht dann in etwa folgendermaßen aus:

bool RaySphereIntersect(VERTEX3D o, d, c, float r)
{
	VERTEX3D l = c - o;
	Float d = l * d;
	float l2 = l * l;
	float r2 = r * r;

	if(d < 0 && l2 > r2) return 0;

	float m2 = l2 - d2;
	if(m2 > r2) return 0;

	q = sqrt(r2 - m2);
	t1 = d-q;
	t2 = d+q;
	return 1;
}
		

Wie Sie sehen, reduziert sich der Aufwand für eine Schnittpunkt­berechnung im Vergleich zur ursprünglichen Implementierung in Ausgabe 10/99 deutlich. Der damalige Ansatz verfolgt gewissermaßen eine analytische Lösung und dient vor allem als Einführung in die Schnittpunkt­berechnungen.

Schnittpunkt­berechnungen vermeiden

Schnelle Algorithmen für effiziente Schnittpunkt­berechnungen sind eine gute Grundlage für einen Raytracer. Bei Szenen mit Tausenden von Objekten wird Ihr Rechner trotzdem unerträglich lange arbeiten, da er für jedes Pixel des Bildes, für jede Rekursions­tiefe und für jeden Schattenstrahl Schnittpunkt­tests mit allen Objekten durchführen muß. Deshalb erzielen Sie bei komplexen Szenen deutliche Geschwindigkeits­steigerungen, wenn Sie sich darüber Gedanken machen, wie Sie Schnitttests ganz vermeiden können.

Nutzen Sie für drei­dimensionale Umgebungen das sogenannte Octrees-Verfahren: Octrees sind baumartige Speicher­strukturen mit jeweils acht Nachfolgern.

Im zwei­dimensionalen Raum läßt sich das Prinzip noch anschaulicher an den dort verwendeten Quadtrees verdeutlichen. Wie ihr Name besagt, besitzen diese jeweils vier Nachfolger.

Stellen Sie sich eine beliebige Anordnung mehrerer Objekte in einer Ebene vor, wie etwa in der Abbildung auf der nächsten Seite links oben. Nun ordnen Sie die Objekte in einer hierarchischen Struktur wie folgt an: Legen Sie ein möglichst kleines Quadrat so um die Objekte, daß diese vollständig darin enthalten sind. Vierteln Sie das Quadrat, und Sie erhalten vier kleinere, im ursprünglichen Quadrat enthaltene Quadrate. Diesen Vorgang wiederholen Sie so lange, bis jedes Quadrat entweder leer ist oder genau ein Objekt enthält. Sie erhalten dann ein Gittermuster.

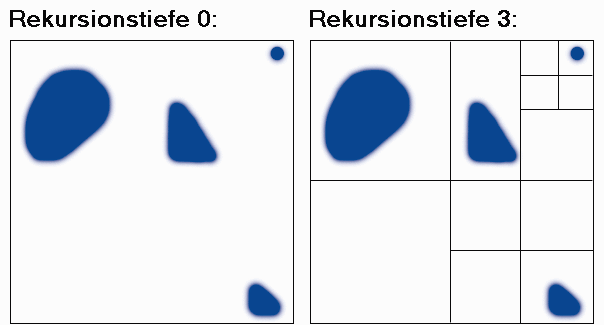
Wollen Sie einen Schnittest eines Strahls mit einem Objekt durchführen, testen Sie nur die Objekte, bei denen Sie auch das dazugehörige Quadrat treffen.Trifft ein Strahl ein Quadrat nicht, so können Sie auch alle Objekte, die in den darin enthaltenen Quadraten liegen, von dem Schnittest ausschließen.

Bei den drei­dimensionalen Octrees teilen Sie einen Würfel rekursiv in seine acht Unterwürfel auf. Um herauszufinden, wieviel Platz ein Primitiv benötigt, geben Sie einen möglichst kleinen Würfel an, der ein Primitiv vollständig enthält. Das gestaltet sich relativ einfach, wenn Sie einen Würfel – eine sogenannte Bounding Box – verwenden, dessen Kanten parallel zu den Koordinaten­achsen verlaufen. Somit sind seine Seitenflächen parallel zu den x/y- und x/z-Ebenen des Koordinaten­systems.

Solche Würfel heißen Axis-Aligned Bounding Boxes (AABBs). Eine AABB legen Sie durch zwei Ortsvektoren fest: Diese geben jeweils die minimalen bzw. maximalen x-, y- und z-Koordinaten an, die das einge­schlossene Primitiv annimmt. Für eine Kugel bestimmen Sie eine AABB also wie folgt:

Kugelmittelpunkt o⃗ = (x,y,z)
Kugelradius r
minV = (x-r, y-r, z-r)
maxV = (x+r, y+r, z+r)
		

Nicht für alle Primitive können Sie ohne weiteres eine AABB bestimmen: Das Ebenenprimitiv besitzt zum Beispiel keine endliche Ausdehnung. Diese speziellen Primitive behandeln Sie deshalb unabhängig vom Octree-Verfahren.

Um den Octree für eine 3D-Szenerie aufzubauen, berechnen Sie die AABBs für alle Primitive, bei denen dies möglich ist. Dann bestimmen Sie einen Würfel, dessen Mitte im Koordinaten­ursprung liegt und der alle AABBs enthält. Nun fügen Sie jedes Primitiv mit einer rekursiven Prozedur in den Octree ein. Die Speicherungs­struktur eines Octree-Würfels bezeichnet man – analog zur Namengebung bei strukturierten Bäumen – als Node (Knoten).

Folgender Pseudecode fügt ein Objekt in den Octree ein:

BOOL InsertObject(OCTREENODE *node, RTObject *o, const EXTEND *e)
{
	Liegt die AABB des Objekts (EXTEND e) in dem Node?
	Wenn nein, return False;
	if (noch nicht maximale Unterteilung)
	{
		Erzeuge 8 Unterwürfel
		Versuche, das Objekt dort einzufügen
	}
	Wenn noch nicht eingefügt, dann in den aktuellen Octreenode einfügen
	return True;
}
		

Den programmierten Code zeigt der Ausschnitt aus der Datei RTOctree.cpp (Listing 1) auf der nächsten Seite oben.

Bei einer Schnittpunkt­berechnung testen Sie einfach rekursiv den Octree mit den darin enthaltenen Objekten. Sie starten an der Wurzel, dem ersten Node des Octrees. Schneidet der Strahl die dazugehörige AABB, berechnen Sie die Schnittpunkte mit den Objekten in diesem Node.

Anschließend rufen Sie die Berechnungs­routine für jeden der acht Subnodes (Unterwürfel) auf. Dadurch schließen Sie bei den meisten Schnittpunkt­berechnungen viele Objekte durch wenige Schnittests mit AABBs aus.

Die Objekte, zu denen Sie keine AABBs berechnen konnten, speichern Sie in einer Liste. All diese Objekte unterziehen Sie wie bisher den Schnittpunkt­tests. Die gesamte Schnittpunkt­berechnung läuft schematisch wie im zweiten Listing auf der nächsten Seite.

Damit haben Sie fast alle Routinen für das Octree-Verfahren zusammen. Es fehlt noch der Schnittest für einen Strahl und eine AABB. Begrenzungs­volumen für Körper wie AABBs sind in der 3D-Grafik ein weit­verbreitetes Mittel für Geschwindigkeits­steigerungen. Daher gibt es für solche Problem­stellungen verschiedene Algorithmen.

Unser Raytracer verwendet die sogenannte Slab-Methode. Diese kommt auch mit Bounding Boxes zurecht, bei denen die Kanten nicht Axis-Aligned sind – also wie die AABBs an den Koordinaten­achsen ausgerichtet. Der Begriff Slab bezeichnet hier zwei parallele Ebenen, die aus Geschwindigkeits­gründen bei der Berechnung gruppiert sind.

Da eine AABB durch drei parallele Ebenenpaare begrenzt wird, können Sie sie durch drei Slabs darstellen. Diese Slabs benennen Sie mit u, v und w. Für ein Slab können Sie – analog zu Ebenen­primitiven – Schnittpunkte berechnen. Da es sich immer um zwei Ebenen handelt, erhalten Sie jeweils einen maximalen und einen minimalen Wert für die Schnittpunkte.

In diese Werte – zum Beispiel t_u_min oder t_v_max – fließt noch der Faktor t aus der Geraden­gleichung ein. Die nächste Berechnung ist dann der eigentliche Trick:

t_min = max(t_u_min, t_v_min, t_w_min);
t_max = min(t_u_max, t_v_max, t_w_max);
		

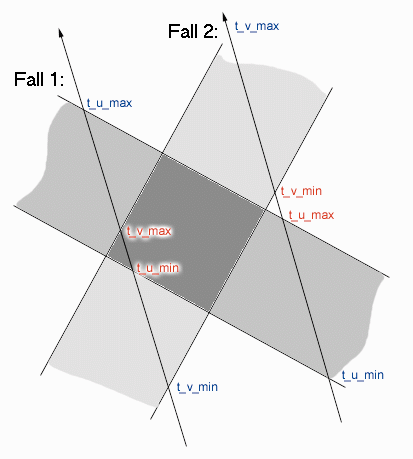
Bei t_min <= t_max schneidet der Strahl die Bounding Box, ansonsten verfehlt er sie. Den Sourcecode zu dieser Routine finden Sie in der Datei RTOctree.cpp. Der einfachere zwei­dimensionale Fall in der Skizze unten veran­schaulicht die Arbeitsweise recht gut.

Auch Slabs sind hier eine Dimension kleiner, also zwei parallele Geraden. In der Grafik sehen Sie eine zwei­dimensionale Bounding Box aus zwei Slabs sowie zwei Geraden, an denen Schnittests durchgeführt werden sollen.

Im ersten Fall ist t_min das Maximum der Werte t_u_min und t_v_min, also t_u_min. Ebenfalls rot gekennzeichnet ist t_v_max, was dem Minimalwert t_max von t_u_max und t_v_max entspricht. Da t_min kleiner als t_max ist, schneidet die linke Gerade die Bounding Box.

Im zweiten Fall ist t_min = t_v_min größer als t_max = t_u_max. Daher zielt die rechte Gerade an der Bounding Box vorbei.

Mit dem fertigen Raytracing-Programm OORT.exe können Sie nun faszinierende Computerwelten entwerfen und beleuchten. Berechnen Sie schöne Bilder damit, und schicken Sie sie uns zu – wir freuen uns auf Ihre Zusendung.

Selbstver­ständlich können Sie das Programm um neue Primitive, Lichtquellen, Beleuchtungs­methoden oder Optimierungen erweitern. Möchten Sie sich weiter über Raytracing informieren, empfehlen wir Ihnen die im Anschluß zitierte Literatur sowie einen Blick in den Sourcecode von POV-Ray. Dessen Webseite finden Sie unter www.povray.org