Poppige Polygone

Carsten Dachsbacher

3D-Grafiken rendern Sie mit Objektmodellen, die aus Dreiecksnetzen aufgebaut sind. Um visuelle Fehler beim Rendering auszuschließen, müssen Sie hohe Anforderungen an die Topologie der Dreiecksnetze stellen. Mit Polygonnetzen stellen Sie in der Computergrafik eine Oberfläche mit Details und schnellen Rendering­techniken dar. Dreiecksnetze sind ein Spezialfall der Polygonnetze: Sie setzen sich aus konvexen oder konkaven Vielecken zusammen. Dreiecksnetze lassen sich mit 3D-Beschleunigern zeichnen, bei parametrischen Flächen – wie den Bézier-Patches – bedarf es einer vorausgehenden Approximation (Annäherung) der Fläche durch Dreiecke.

Der Detailreichtum hängt vom Blickwinkel und der Entfernung zum Betrachter ab. Um Details eines 3D-Objekts mit 10 000 Dreiecken sehen zu können, muss das Objekt sich in kurzer Distanz zum Betrachter befinden. Doch betrachten Sie das Objekt von weitem, genügt eine gröbere Repräsentation des Objektumrisses. Es genügen dann vergröbernde Objekte mit wenigen 100 Polygonen.

Sie beschleunigen Ihre 3D-Grafik, indem Sie Details weglassen. Im folgenden zeigen wir Ihnen Schritt für Schritt, wie Sie vorgehen müssen, um schöne Dreiecksnetze zu erhalten.

Tessellierung

Polygone können in beliebiger Form und Anzahl von Eckpunkten auftreten, einfach gesagt als Vielecke. 3D-Beschleuniger rendern jedoch nur Dreiecke, in die Sie die Polygone zerschneiden müssen. Tesslierung bezeichnet den Prozess, wenn Sie ein Polygon in mehrere aufteilen. Die meisten 3D-Modelling-Programme liefern Dreiecksnetze, bei denen eine Tessellierung nicht zweckmäßig ist, allerdings gibt es auch andere Quellen von 3D-Daten wie von Scannern. Wenn Programme Polygone generieren, bezeichnet man dies als prozedurales Modelling. Auch 3D-Scanner liefern Polygondaten.

Beim Rendern von Landschaften liegt anfangs nur eine zwei­dimensionale Karte mit Höhen­informationen vor. Daraus Polygondaten zu erzeugen, ist auch eine Form des prozeduralen Modellings. Sie tessellieren Polygonnetze zu Dreiecksnetzen, weil die Grafik-APIs OpenGL und Direct3D so arbeiten. Wenn Sie das Polygonnetz zu Dreiecken tessellieren, spricht man von Triangulierung.

Polygone sollten Sie auch tessellieren,
• wenn der Renderer nur konvexe Polygone beherrscht,
• oder die Fläche in annähernd gleich große Flächen unterteilt werden soll, um Schatten­effekte oder Radiosity-Berechnungen durchzuführen.

Ein robustes Programm zu schreiben, das für alle denkbaren Polygonnetze funktioniert, ist schwierig. Das liegt an den vielen Spezialfällen, die auftreten können. Eine weitere Schwierigkeit bei geometrischen Algorithmen sind Rundungs­probleme. Funkt­ionierende Algorithmen mit Sourcecodes finden Sie in unseren Literatur­angaben und Links (unten).

Sie können es sich leichter machen, wenn Sie sich auf zwei Dimensionen beschränken. Dazu projizieren Sie das Polygon auf eine Ebene. Meistens genügt eine der drei Ebenen, die durch das Koordinaten­system aufgespannt werden. Wählen Sie diejenige Ebene, auf der das zwei­dimensionale Pendant die größte Fläche hat. Schwierig wird es, wenn das Polygon in sich verdreht ist: Das projizierte Polygon kann Kanten besitzen, die sich gegenseitig schneiden.

Schattierungsprobleme

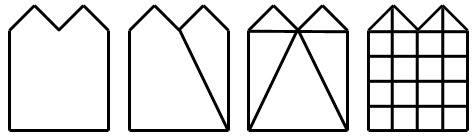
Um 3D-Polygonnetze darzustellen, die aus Vierecken bestehen, müssen Sie sie in Dreiecke konvertieren. Konvexe Vierecke können Sie in zwei Dreiecke aufteilen, indem Sie sie an einer der beiden Diagonalen trennen. Wenn ein Viereck konkav ist (nach innen gewölbt), schneiden Sie es an der Schnitt­diagonalen in zwei Dreiecke.

Das Bild oben zeigt ein Quadrat, das links mit Raytracing dargestellt und schattiert ist. Die anderen Quadrate wurden mit einem 3D-Beschleuniger gezeichnet. Das mittlere Quadrat wurde entlang der Diagonalen von links unten nach rechts oben aufgeteilt.

Mit verschiedenen Ansätzen entscheiden Sie sich für die richtige Diagonale, wobei Sie geeignet gewählte Differenzen minimieren. Wenn Sie über keine Attribute wie Farbe oder Normale verfügen, wählen Sie die kürzere der beiden Diagonalen. Kennen Sie die Farb- oder Helligkeits­werte an den Eckpunkten, entscheiden Sie sich für die Diagonale mit dem geringeren Helligkeits­unterschied der Eckpunkte.

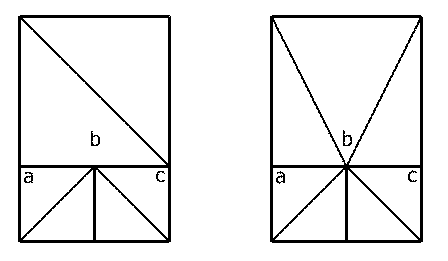
Bei Landschafts­modellen liegen Daten einer zwei­dimensionalen Karte mit Höhen­informationen vor, mit der Sie ein Netz von Rechtecken aufbauen. Diese müssen Sie zum Zeichnen wieder in Dreiecke umwandeln. Auch hier ist es nicht sinnvoll, entlang der gleichen Diagonale zu teilen. Als Kriterium können Sie den Höhenwert an den Eckpunkten oder den Winkel zwischen den resultierenden Polygonen heranziehen.

Das Bild oben rechts teilt alle Rechtecke entlang derselben Diagonale auf. Im unteren Teil wurde entlang der Diagonalen mit geringerem Höhen­unterschied geteilt. Rechts im Bild wird der Punkt b von den unteren Dreiecken verwendet, im Quadrat daneben ist er nicht beteiligt. An diesem Punkt treten T-Vertizes auf: Die Kanten um den Knoten b haben die Form eines T. Beheben können Sie das nur, indem Sie die T-Vertizes identifizieren und das obere Rechteck tessellieren.

Konsolidierung

Die Tessellierung liefert Ihnen viele Dreiecke, die Sie rendern können. Um schneller und besser zu rendern, suchen Sie Verbindungen und Gemeinsam­keiten von Polygonen. Dieser Vorgang heißt Konsolidierung.

Effizient ist es, Polygone zu Polygonnetzen zu gruppieren. Ein solches Netz besteht aus Vertizes und Polygonkanten. Die meisten Vertizces werden nicht nur einmal benötigt, sondern sind Bestandteil mehrerer Polygone. Diese Netze bringen eine Reihe von Vorteilen für das Rendering mit sich:
• Sie benötigen weniger Platz, da Sie mehrfach verwendete Knoten nur einmal speichern müssen.
• Sie müssen weniger Vertizes beim Rendering transformieren. Unterstützung beim Rendering solcher Netze erhalten Sie durch vertex buffers in Direct 3D oder vertex arrays in OpenGL.

• Backface Culling (von hinten sehen) erhöht die Geschwindig­keit. Dabei gehen Sie davon aus, dass Ihr Polygonnetz eine geschlossene Oberfläche bildet, also ein solider Gegenstand (Kugeln oder Würfel) modelliert wurde.

Wenn Sie bei einem Dreieck zwischen Vorder- und Rückseite unterscheiden können, platzieren Sie die Dreiecke mit der Vorderseite nach außen. Der Vorteil: Dreiecke, die Sie von hinten sehen (Backface Culling), zeichnen Sie nicht, weil sie durch näher liegende Dreiecke (von vorne zu sehen) verdeckt wären. Polygonnetze, die geschlossen sind, und Backface Culling erlauben, werden auch als manifold oder closed bezeichnet.

Ob ein Polygon von vorne oder von hinten zu sehen ist, entscheiden Sie anhand der Normalen des Polygons. Die meisten 3D-Programme exportieren die Orientierung der Polygone entweder explizit durch Angabe einer Normalen oder implizit durch eine feste Reihenfolge der Eckpunkte. Meistens sehen Sie ein Polygon von vorne, wobei die Eckpunkte gegen den Uhrzeigersinn angegeben werden. Das nennt man Entscheidung anhand der Normalen­richtung. In diesem Fall sehen Sie die Eckpunkte gegen den Uhrzeigersinn angeordnet, und die Normale zeigt zum Betrachter hin. Sie sehen das Polygon von vorn. Dieser Zusammenhang ergibt sich, da die Richtung der Normalen (Vorzeichen) von der Reihenfolge der Eckpunkte abhängt. Fehlen Informationen über die Orientierung der Polygone, müssen Sie selbst für die Konsistenz der Normalen sorgen.

Sie müssen auch dafür sorgen, dass die Normalen nach außen zeigen. Diese beiden Punkte sind fürs Backface Culling und die Beleuchtungs­effekte wichtig. Meistens repräsentieren Polygonnetze eine gekrümmte Oberfläche, besitzen aber keine Normalen­vektoren an den Vertizes. Manchmal stoßen verschieden gekrümmte Oberflächen aneinander. Dann achten Sie beim Generieren von Normalen darauf, dass eine solche Kante nicht verschwindet. Im Bild sehen Sie den Punkt, den Sie beachten müssen, damit die Kante bei der Beleuchtung erhalten bleibt. Polygone müssen Sie entsprechend der Oberflächen­teile, zu denen Sie gehören, gruppieren. Solche Gruppen bezeichnet man als Smooth Groups.

Diese Aufgaben stellen sich, wenn Sie 3D-Objekte perfekt zeichnen wollen. Sie lösen diese Aufgabe, indem Sie die folgenden Stichpunkte abarbeiten.
• Sie bilden einer Kantenliste mit einem Verweis auf Polygone.
• Sie suchen Gruppen aneinander­liegender Polygone.
• Sie gewährleisten die Konsistenz der Orientierung innerhalb der
Gruppen. • Sie stellen fest, was inner- und außerhalb des 3D-Modells ist.
• Sie bestimmen die Smooth Groups.
• Sie bilden daraus Polygonnetze.

Was sich hinter diesen Punkten versteckt, erläutern wir in den weiteren Details. Für diese Arbeit liegen die Polygone bereits tesselliert vor.

Liegen zum Beispiel Daten für Smooth Groups, Konsistenz oder Orientierung vor, sparen Sie sich die entsprechenden Arbeits­schritte. Zuerst listen Sie alle Kanten in den Polygonen auf. Für jede Kante speichern Sie Verweise auf die Polygone. Die Kanten geben Sie durch Start- und Endpunkte an. Wählen Sie den Startpunkt, der die niedrigere x-Koordinate hat, oder bei gleicher x-Koordinate den Punkt mit niedrigerer y-Koordinate. Bei identischen Eckpunkten werfen Sie die Kante weg. Mit ermittelten Start- und Endpunkten beseitigen Sie identische Kanten. So erhalten Sie eine Liste, in der jede Kante nur einmal vorkommt.

Aneinander­liegende Polygone teilen Kanten. Anhand der Nachbarschafts­beziehungen identifizieren Sie die Polygongruppen. Ein Datensatz kann mehrere dieser Gruppen (Flächen) besitzen. Das Modell der Teekanne besteht aus Gruppen für die Kanne, dem Griff und dem Deckel.

Nun sichern Sie die Konsistenz der Orientierung. Ordnen Sie die Eckpunkte aller Polygone gegen den Uhrzeigersinn. Wählen Sie in jeder Gruppe ein Startpolygon. Überprüfen Sie die Orientierung in jedem Nachbarpolygon. Der Test ist einfach: Beide Polygone haben eine gemeinsame Kante mit einem Start- und Endpunkt. Wenn die Richtung der Kante in beiden Polygonen übereinstimmt, drehen Sie die Orientierung im Nachbarpolygon um. Mit den Nachbar­polygonen verfahren Sie rekursiv weiter, bis Sie alle Polygone der Gruppe geprüft und korrigiert haben. Rekursiv bedeutet, mit den Nachbar- wie mit dem Startpolygon zu verfahren.

Ob eine Gruppe von Polygonen ein geschlossenes Netz bildet, stellen Sie folgendermaßen fest: Zählen Sie, wie oft jede Kante in Ihrem Netz vorkommt. Wenn diese Zahl 0 oder geradzahlig ist, ist das Netz geschlossen.

Entscheiden Sie, welche Seite eines Polygonnetzes nach außen zeigen soll. Mit folgender Methode erarbeiten Sie, welche Punkte innerhalb und welche außerhalb des 3D-Objekts liegen. Sie nutzen einen Algorithmus, der fast immer zum Ergebnis führt. Sie müssen die Normalen oder die Orientierung eines Polygonnetzes umdrehen, wenn die Normalen nach innen zeigen. Ob das nötig ist, verrät Ihnen der Algorithmus des vorzeichen­behafteten Volumens. Ist das Vorzeichen negativ, ändern Sie die Orientierung der Polygone.

Das Volumen berechnen Sie so: Zuerst bestimmen Sie die Bounding Box (ein möglichst kleiner Quader im Raum, in dem das Polygonnetz Platz findet). Die einfachste Rechnung führt schon zu ausreichenden Ergebnissen: Sie beschränken sich bei der Berechnung der Bounding Box auf die so genannten Axis Aligned Bounding Boxes (AABB). Bei AABBs liegen alle Kanten des Quaders parallel zu den Achsen des Koordinaten­systems. Sie können die AABBs durch die jeweils kleinsten und größten x-, y- und z-Koordinaten bestimmen, die in den betrachteten Polygonen vorkommen. Für die weiteren Berechnungen betrachten Sie den Mittelpunkt der Bounding Box. Zeichnen Sie gedanklich für jedes Dreieck des Netzes einen Tetraeder mit dem Dreieck als Grundfläche und dem Mittelpunkt als Spitze. Das Volumen eines Tetraeders berechnen Sie nach der Formel

1/3 Grundfläche x Entfernung von Spitze und Grundfläche

Die Entfernung enthält das Vorzeichen des Volumens. Dies ist negativ, wenn die Normale zur Spitze zeigt. Die Summe aller Tetraeder-Volumina bilden das Volumen des Dreiecksnetzes. Den Faktor von einem Drittel können Sie weglassen, um Rechenzeit zu sparen. Für Sie ist das Vorzeichen der Summe wichtig, welches sich nicht durch Faktoren ändert.

Bilden Sie die Smooth Groups, wenn Ihr Modelling-Programm diese nicht ausweist. Die Polygone, zwischen deren Normale ein festgelegter Grenzwinkel nicht überschritten wird, gehören zu einer Smooth Group. Wenn Sie eine Kante zwischen zwei Smooth Groups behalten, spricht man von edge preservation: Sie sehen beim Schattieren eine harte Kante. Befinden sich zwei benachbarte Polygone in derselben Smooth Group, teilen Sie die Vertex-Normalen entlang ihrer gemeinsamen Kante.

Als Spezialfall stellen Sie sich einen Kegel vor. Dessen Polygone fassen Sie in einer Smooth Group zusammen, wenn Sie mit Grenzwinkeln arbeiten. An der Spitze finden Sie nur einen Vertex mit einer Normalen. Rendering­fehler in der Beleuchtung kann das Modelling­programm nur lösen, wenn es eine Vertex-Normale liefert oder ein winziges Stückchen von der Spitze abschneidet, um mehrere Vertizes zu erzwingen.

Wenn Sie alle Arbeits­schritte durchgeführt haben, fassen Sie das Polygon zu Polygonnetzen zusammen. Meistens können Sie die Shared-Vertex-Struktur verwenden, um die Netze zu speichern. Direct3D und OpenGL unterstützen Sie dabei. Legen Sie eine Liste von Vertizes an. Für jeden Vertex speichern Sie seine Koordinate, seine Normale für die Beleuchtungs­berechnung und eventuell andere Attribute wie Farbe und Textur­koordinaten.

In einer weiteren Liste speichern Sie für jedes Polygon drei Indizes. Diese Indizes verweisen auf die Vertizes in der ersten Liste. Wenn es die Anwendung erfordert, speichern Sie in der Polygonliste Informationen wie die Polygonnormale für das Backface Culling oder einen Verweis, welche Textur zugewiesen wurde.

Nach diesen Vorbereitungen haben Sie ein Polygonnetz , das Sie korrekt beleuchten und zeichnen können.