Polygonnetze in Vollendung

Carsten Dachsbacher

Beim Rendering von 3D-Modellen ist es hilfreich, ein Modell in mehreren Auflösungs­stufen zu betrachten oder während der Ansicht (on the fly) beliebige Detailstufen davon zu erzeugen. Bei Objekten, die weiter vom Betrachter entfernt sind, genügen grobe Darstellungen, da die Details wegen der begrenzten Bildschirm­auflösung nicht mehr sichtbar sind.

Detaillierte 3D-Modelle transportieren Sie über Netzwerke oder via Internet, indem Sie das Dreiecksnetz „progressiv“ übertragen: Mit den bereits übertragenen Daten erzeugen Sie eine Art Vorschau auf das fertige Modell. Die Vorschau wird so lange verfeinert, bis das Original­dreiecksnetz wiederher­gestellt ist. Eine Anwendung der progressiven Übertragung kennen viele, die JPEG-Dateien im Internet betrachten. Zuerst sehen Sie ein grobes Bild. Mit fort­schreitender Übertragung erkennen Sie Details. Am einfachsten lassen sich 3D-Modelle progressiv übertragen und anzeigen, indem Sie verschiedene Detailstufen anlegen, die Sie unabhängig voneinander übertragen. Schöner und effizienter ist es, ein grobes Netz und Informationen zu übertragen, die von sich aus Details herausarbeiten.

Um Dreiecksnetze zu speichern, verwenden Programmierer meist die Struktur Naive Shared Vertex. Diese speichert eine Liste von Knoten und eine für Dreiecke mit jeweils drei Indizes auf Knoten.

Sofern diese Darstellung keine Attribute wie Textur­koordinaten oder Vertex-Normalen berücksichtigt, braucht die Information der Topologie ungefähr doppelt so viel Speicherplatz wie die der Geometrie. Diese Abschätzung gilt bei genügend großen Netzen. Die Topologie ordnet Vertizes den Kanten und Polygonen zu. Die Geometrie­information begnügt sich mit den Koordinaten der Vertizes.

Im Verlauf der Reduktion von Dreiecksnetzen berechnen Sie vergröberte 3D-Modelle, die die Originalform bestmöglich approximieren. Dabei erzeugen Sie eine andere Struktur für die Speicherung: die Progressive Meshes.

Dreiecksnetze reduzieren

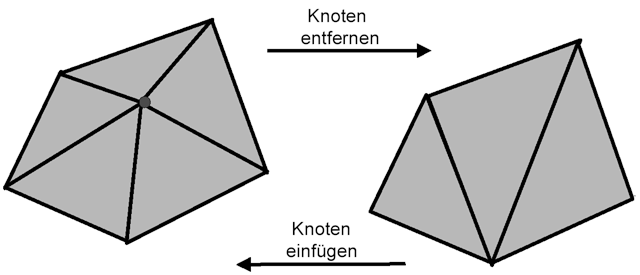
Details aus Dreiecksnetzen lassen sich auf verschiedene Arten entfernen. Alle Arten reduzieren die Zahl der Vertizes und Polygone.

• Die erste Methode wählt einen Punkt, der mit seinen Nachbarpunkten Dreiecke bildet, und entfernt diesen. Durch den fehlenden Vertex fallen eine Reihe von Dreiecken weg, wobei ein Loch im Dreiecksnetz entsteht. Dieses Loch, auch Patch genannt, füllen Sie mit neuen Dreiecken aus, wobei Sie den gerade entfernten Vertex nicht mehr verwenden. Diese Operation nennt sich Knoten entfernen/einfügen (Vertex removal/insertion). Sie reduzieren bei jeder Anwendung dieses Operators die Zahl der Vertizes um 1, die Zahl der Dreiecke um 2.
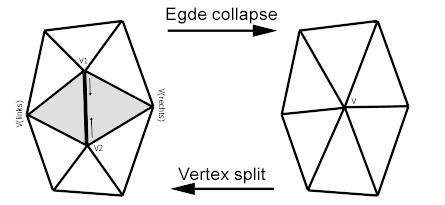
• Eine zweite Methode bietet der EdgeCollapse/Vertex-Split-Operator. Das Verfahren wählt zwei durch eine Kante verbundene Vertizes und ersetzt sie durch einen neuen gemeinsamen Vertex. Auch hier reduzieren Sie das Dreiecksnetz um zwei Dreiecke und einen Vertex. Da Sie bei der progressiven Übertragung, die diesen Operator verwendet, die vereinfachten Dreiecksnetze wieder verfeinern wollen, müssen Sie die Informationen für die Verfeinerung speichern. Dazu benötigen Sie Informationen, welcher der neue Vertex v ist, welche er zu ersetzen hat (v1 und v2), und mit welchen Nachbar-Vertizes v(links) und v(rechts) die Dreiecke wiederher­gestellt werden müssen. Sie speichern also für jede Anwendung des Operators eine Datenstruktur mit

Edge Collapse Information:
	v v1 v2 v(links) v(rechts)
		

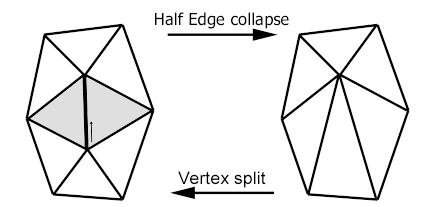
• Eine Variante des Edge Collapse ist der Half Edge Collapse. Dabei wird kein neuer Punkt v berechnet, sondern einer der Ausgangspunkte gewählt. In diesem Fall speichern Sie nur folgende Informationen:

Half Edge Collapse Information:
	v1 v2 v(links) v(rechts)
		

Bei der schrittweisen Vergröberung Ihres Dreiecksnetzes sind stets zwei Entscheidungen zu treffen: welche Kante als nächste entfernt werden soll und wo der neue Punkt (beim Edge Collapse) liegt oder welchen der beiden Kantenpunkte Sie beibehalten wollen (beim Half Edge Collapse). Beide Entscheidungen beeinflussen die Qualität der erzeugten 3D-Objekte.

Betrachten Sie zuerst die Suche nach der Kante, deren Verlust das 3D-Objekt möglichst wenig beeinflusst. Zwar sind alle Methoden heuristischer Natur, denn Sie können nicht berechnen, wie stark eine entfernte Kante den visuellen Eindruck des 3D-Objekts auf den Menschen stört. Deshalb gibt es verschiedene Ansätze. Sie berechnen einen Kostenwert für jede mögliche Kanten­entfernung. Hohe Kosten bedeuten, dass die Heuristik eine Kante als wichtig für das Erscheinungs­bild des 3D-Objekts wertet.
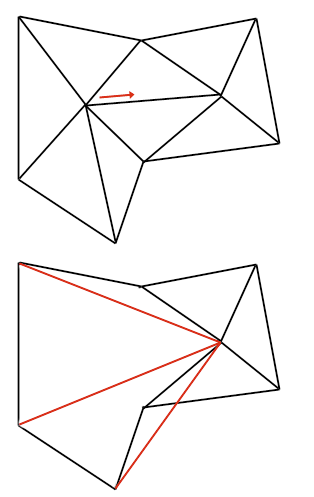
• Nach der Methode, die auch das Beispiel-Programm auf der Heft-CD anwendet, berechnen Sie die Länge der Kante, zu der Sie die Kosten wissen wollen. Anschließend suchen Sie die zwei Nachbar­dreiecke und berechnen den Winkel zwischen deren Normalen. Als Kosten betrachten Sie das Produkt aus Länge der Kante und Winkel. Wenn Sie eine Kante entfernen wollen, wählen Sie jeweils die Kante mit den niedrigsten Kosten. Allerdings müssen Sie auch einen Spezialfall beachten und nicht blind dem Kostenwert vertrauen. Es kann passieren, dass Sie durch das Entfernen einer Kante die neuen Kanten mit den alten schneiden. Dieser Fall tritt meist auf, wenn Sie das 3D-Objekt zu stark reduzieren.

Beim Edge Collapse müssen Sie den neuen Vertex richtig platzieren. Das bekannteste Verfahren dazu stammt von Michael Garland und Paul S. Heckbert, ist beschrieben in Surface Simplification Using Quadric Error Metrics (siehe Literaturhinweis am Ende) und arbeitet mit einer Kostenfunktion für die Vertex-Platzierung. Dabei berechnen Sie die Kosten, die entstehen, wenn Sie die beiden Vertizes der Kante (v1 und v2) zum neuen Vertex v verschieben. Bei der verwendeten Kostenfunktion kann der Vertex v irgendwo auf der Geraden, die durch v1 und v2 festgelegt ist, liegen.

Die Kostenfunktion ist wie folgt definiert: Jeder Vertex wird von einer Reihe Dreiecke geteilt. Jedes dieser Dreiecke liegt in einer Ebene. Als Kosten verwenden Sie die Summe der quadrierten Abstände zwischen den Ebenen und der neuen Position. Die Gesamtkosten eines neuen Vertex sind die Kosten für die Verschiebung von v1 plus der von v2. Eine beispielhafte Implementation mit Sourcecode dieses Verfahrens finden Sie auf der Website von Michael Garland. Wenn Sie nur einen Half Edge Collapse durchführen wollen, können Sie sich mit der beschriebenen Kostenfunktion für einen Vertex entscheiden. Die Kosten ergeben sich aus der Verschiebung des einen Vertex auf den anderen.

Progressive Meshes

Mit dem Progressive-Mesh-Verfahren erzeugen Sie schnell beliebige Detailstufen, wobei Sie sogar in Echtzeit Dreiecksnetze übertragen können. Es arbeitet nur mit Half Edge Collapses.

Für das erste Ziel speichern Sie zusätzliche Daten: Sie müssen die Reihenfolge, in der Sie Vertizes entfernen, speichern (also eine Permutations­tabelle). Für jeden Vertex, den Sie entfernen, müssen Sie die Information aufheben, zu welchem Vertex er hingewandert ist (Map-Tabelle). Die Objekt­reduktion im Pseudocode:

v = Anzahl Vertizes
while(v > 0)
{
	suche Kante mit kleinsten Kosten
	Vertex u sei der zu entfernende

	speichere: Vertex u nach Index v
		permutation[index u] = v;

	speichere:
		collapse_map[v] =
			Index des anderen KantenVertizes
	v--;
}
		

Anhand der Permutations­tabelle müssen Sie die Vertizes des 3D-Objekts umsortieren und die Indizes der Dreiecke (bei der Shared-Vertex-Struktur) anpassen:

for(alle Vertizes)
	pVertexList_neu[permutation[i]] =
		pVertexList[i];

for(alle Polygone)
	for (alle Indizes)
		index_neu =
			permutation[index_alt];
		

Wenn Sie das 3D-Objekt zeichnen wollen, können Sie festlegen, wie viele Vertizes das neue Dreiecksnetz haben soll. Die Zahl der Dreiecke geben Sie nicht direkt an. Mit Hilfe der Map-Tabelle können Sie nachvollziehen, welche Vertizes entfernt und auf welche verschoben wurden. Wenn ein Dreieck (Bild S. 266 oben) aus v1, v2 und v(links) besteht und v1 auf v2 verschoben wurde, würden Sie aus der Map-Tabelle auslesen, dass v1 zu v2 wurde. Für das resultierende Dreieck ergäben sich die Eckpunkte v2, v2 und v(links). Solche degenerierten Dreiecke, bei denen zwei oder drei Eckpunkte zusammenfallen, zeichnen Sie nicht.Der Pseudocode zeigt die komplette Zeichenroutine. mx ist die neue Anzahl der Vertizes im Objekt:

int remap(int idx,int mx)
{
	while(idx >= mx)
	idx = collapse_map[idx];
	return idx;
}

for(alle Dreiecke)
{
	p0 = remap(Index 1);
	p1 = remap(Index 2);
	p2 = remap(Index 3);
	if(p0 == p1 || p1 == p2 || p2 == p0)
		gehe zu nächstem Dreieck
	Zeichne Dreieck mit p0, p1, p2
}
		

Die zweite Anwendung der Progressive Meshes ist, Dreiecksnetze progressiv zu übertragen. Dabei übertragen Sie zuerst ein grobes Modell, das Sie am Ende Ihres Reduktions­vorgangs erhalten haben. Anschließend übertragen Sie nur noch die Half-Edge-Collapse-Information. Damit kann das Originalmodell wieder vollständig hergestellt werden. Bei der Übertragung von Dreiecksnetzen werden für die Koordinaten der Vertizes meistens keine drei Floats investiert. Stattdessen quantisieren Sie die Koordinaten. Das heißt, Sie stellen die Koordinaten durch Integer-Werte mit weniger Bits pro Koordinate dar. Dazu berechnen Sie die Ausdehnung des Objekts entlang der x-, y- und z-Achse, skalieren die Float-Werte auf einen genügend großen Zahlenbereich und runden anschließend. Folgendes Beispiel zeigt die Quantisierung einer Achse auf 12 Bit:

finde min+max Koordinate,
(min_x und max_x)
Ausdehnung = max_x - min_x
Skalierung = (2 ^ 12) / Ausdehung

for (jede Koordinate)
	quantisierte Koordinate =
		(Floatkoordinate - min_x) *
		Skalierung
		

Das Netz verfeinern

Um die Auflösung des Dreiecksnetzes (also die Zahl der Vertizes, Kanten und Dreiecke) zu erhöhen, um Details am Objekt zu modellieren oder numerische Simulationen mit hoher Rechen­genauigkeit durchzuführen, verfeinern Sie die Maschen des Netzes.

Beim Mesh Refinement (Netzver­feinerung) unterscheidet man zwischen dem globalen (Uniform Refinement) und dem adaptiven Verfeinern (Refinement). Das globale Verfeinern ist für alle Dreiecke identisch.

Sie verfeinern Dreiecksnetze, indem Sie die Dreiecke in mehrere kleine zerschneiden. Es erhöht die Genauigkeit der Darstellung, wenn keine langen, schmalen Dreiecke, sondern möglichst gleichseitige entstehen: Edge-Splitting (auch 1-to-4 split genannt) und sqrt(3)-subdivision.

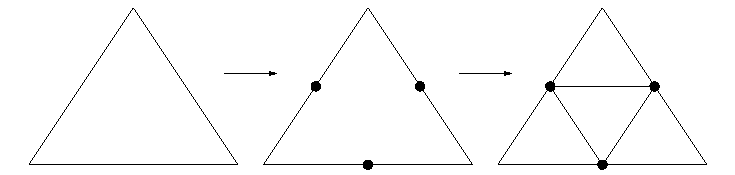
• Beim 1-to-4-split-Verfahren fügen Sie neue Vertizes an den Mittelpunkten der Kanten ein, die Sie zu einem neuen Dreieck verbinden. Sie erhalten vier mal so viele Dreiecke, wenn Sie das mit dem gesamten Netz machen.

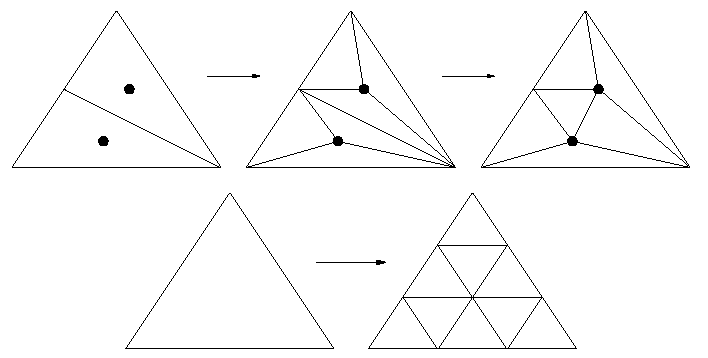
• Bei der sqrt(3)-Subdivision betrachten Sie zwei benachbarte Dreiecke. Sie fügen jeweils einen Vertex im Mittelpunkt der Dreiecke ein und verbinden ihn mit den Eckpunkten. Nun drehen Sie die alte Kante zwischen den Original­dreiecken, um die beiden neuen Vertizes zu verbinden. Wenn Sie diesen Vorgang zweimal auf ein Dreieckspaar anwenden, teilen Sie die Originalkanten in drei Strecken auf.

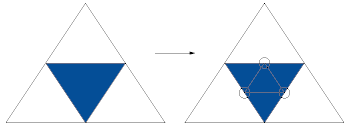
Es ist nicht immer notwendig, alle Dreiecke des Netzes zu zerschneiden. Behandeln Sie zunächst nur die Dreiecke, die Sie verfeinert benötigen.

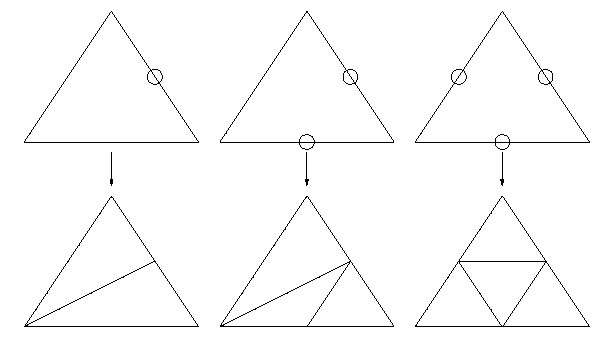
Dadurch können T-Vertizes an Grenzen zu den benachbarten Dreiecken entstehen. Diese vermeiden Sie im Refinement-Prozess mit einer Schließungs­operation: Unterteilen Sie die Nachbar­dreiecke (eins, zwei oder alle drei).

Dreiecksnetze glätten

Mit jedem Bildbear­beitungsprogramm können Sie ein Bild weich zeichnen, wodurch es unscharf erscheint. Das funktioniert auch mit Dreiecksnetzen (Mesh Relaxation = Entspannung).

Anders als bei Bitmaps lassen sich nicht einfach Farbwerte mitteln und ändern. Objekt­koordinaten stellen kein Pendant zu Pixeln dar, weil Sie zusätzlich die Topologie-Information berück­sichtigen müssen. Wie der Name des Verfahrens andeutet, geht es darum, Spannung aus den Dreiecksnetzen zu nehmen. Spannung tritt an Stellen auf, an denen Spitzen hervorragen. Betrachten Sie jeden Vertex, und ziehen Sie ihn ein Stück zu jedem seiner Nachbarn hin.

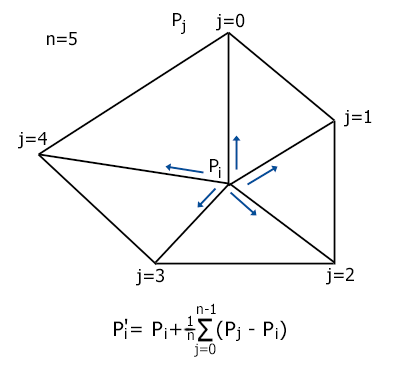
Ein Beispiel: Die Nachbar-Vertizes bilden eine mehrseitige Pyramide mit dem aktuell betrachteten Vertex als Spitze, dann zieht der Algorithmus den Vertex in Richtung der Grundfläche. So glätten Sie das Dreiecksnetz. Wenn alle Vertizes (inklusive des betrachteten) in einer Ebene liegen, können Sie zwar den Vertex verschieben, aber ändern dadurch nicht die Form des Objekts. Trotzdem hat das Verfahren einen positiven Aspekt: Die Dreiecke des Netzes verändern durch die neuen Vertex-Positionen ihre Form in Richtung gleichseitiger Dreiecke. Dieses Verfahren verwenden Sie für numerische Simulationen. Die Formel, nach der Sie die Vertizes verschieben, verdeutlicht das Bild unten.

Der Pseudocode meshrelax.c veran­schaulicht das Vorgehen. Sie benötigen zwei Speicher­bereiche für die Vertizes: einen für die alten und einen für die neuen Positionen.

Mit Mesh Relaxation runden Sie die Kanten eines Würfels ab. Vor dem Glätten wurde das Dreiecksnetz des Würfels mehrmals mit einem 1-to 4-split geteilt. Ansonsten wäre die Darstellung nicht detailliert genug, um eine Glättung erkennen zu können.

Mit den vorgestellten Methoden können Sie 3D-Modelle feiner oder gröber berechnen, ohne Software Dritter zu benutzen.