Licht in Echtzeit

Carsten Dachsbacher

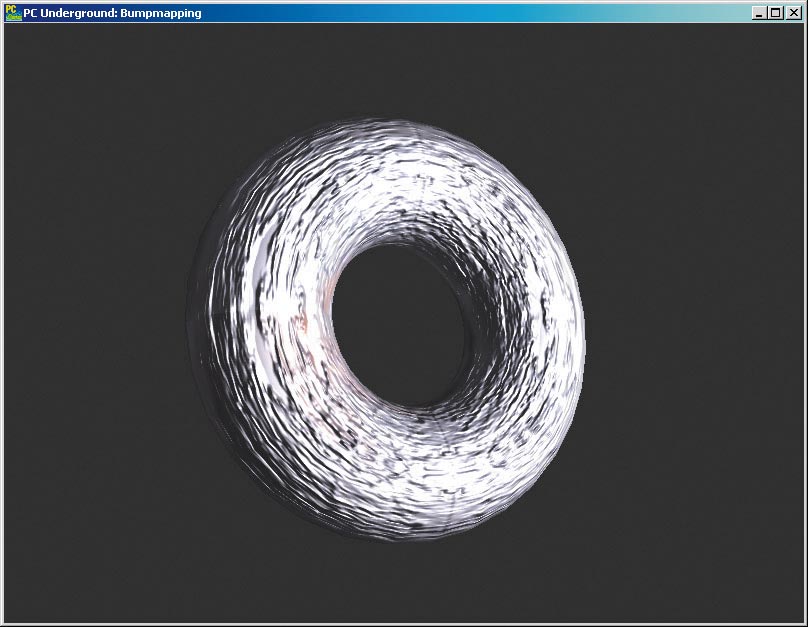
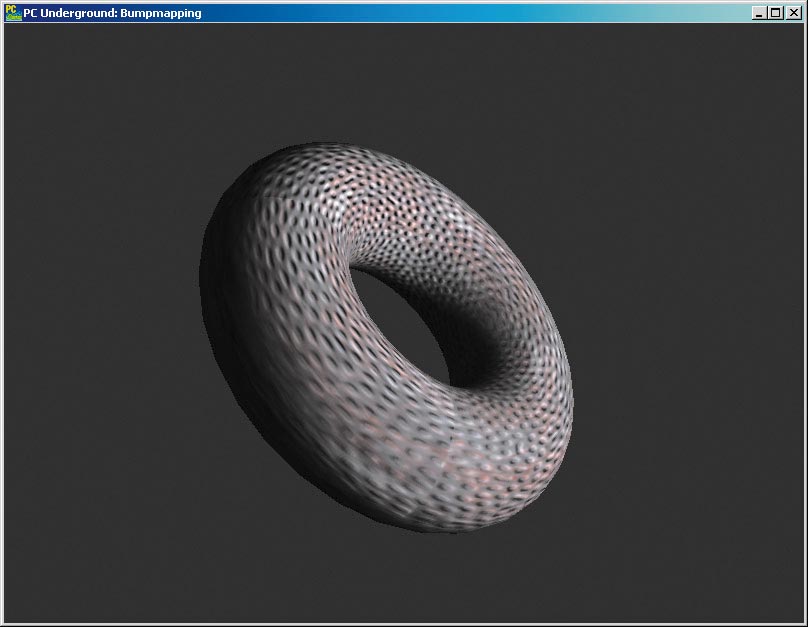
3D-Hardware-Entwickler bieten ständig neue Optionen an, die die 3D-Grafik-Programmierer ausfüllen müssen. Dazu gehört auch das von moderner Hardware unterstützte Bumpmapping in OpenGL: ein Verfahren, das den realistischen Eindruck von 3D-Objekt­oberflächen unterstreicht. Anders als Texture-Mapping, das auf die Farbe der Objektober­flächen abzielt, wird Bumpmapping dazu verwendet, Unebenheiten der Oberflächen­struktur zu rendern. Im Bild unten sehen Sie einen Torus als Drahtgitter­modell, texturiert und mit Bumpmapping.

Mit Bumpmapping können Sie Beulen auf der Oberfläche von 3D-Objekten darstellen. Objekte in einer so hohen geometrischen Auflösung zu rendern, um solche Effekte zu erzielen, ist sehr rechenzeit- und speicher­intensiv. Abgesehen davon, sind die Unebenheiten im Vergleich zur groben geometrischen Form eines Objekts sehr klein. Nehmen Sie als Beispiel das 3D-Modell eines Holztisches. Die Unregel­mäßigkeiten auf der Tischfläche sind klein im Vergleich zur ihrer ebenen Form. Deshalb liegt es nahe, nicht die Geometriedaten selbst so fein zu gestalten.

Theorie des Bumpmapping

Der wichtige Punkt beim Bumpmapping ist: Nur die Beleuchtungs­berechnung lässt die Unebenheiten sehen. Diese sind geometrisch nicht im Dreiecksnetz vorhanden. An den geraden Kanten eines mit Bumpmapping gerenderten 3D-Objekts sehen Sie, dass dessen Form selbst nicht verändert wird.

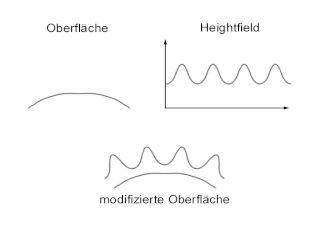
Die Idee des Bumpmapping wurde 1978 von James Blinn entwickelt. Bumpmapping ist ein rein textur­basierendes Rendering-Verfahren, um Unebenheiten auf Oberflächen durch die Beleuchtung zu simulieren. Die Unebenheiten werden in einer Graustufen­textur (Graustufen-Bitmap) als Heightfield angegeben, deren Auswirkung Sie im Bild sehen.

Der Grafiker schafft nur die Graustufen-Bitmap. Daraus generiert der Programmierer Daten, wie diese für das verwendete Bumpmapping-Verfahren nötig sind. Von diesen Verfahren stellen wir eines vor, dass neuere Hardware wie die GeForce GPUs von nVidia benötigt. Anschließend zeigen wir Ihnen einen relativ alten Ansatz, der auf jeder 3D-Hardware funktioniert.

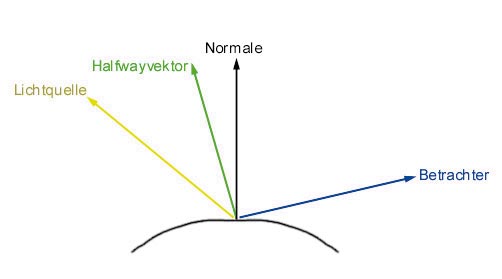
Die Theorie der Beleuchtungs­berechnung zeigt, wo das Bumpmapping ansetzt. Beleuchtung berechnen Sie aus Formeln, welche Sie mit der Vektorrechnung darstellen und verdeutlichen. Mit einer vereinfachten Formel, berechnen Sie diffuse und spiegelnde Reflexionen. Diese Formel entstammt dem Blinn-Beleuchtung­smodell, das wie das Phong-Modell empirisch ermittelt wurde.

C = (max(0,(L*N))
	+ max (0,(H*N))^n)
	x Dl x Dm
		

Blinn und Phong sind als Grundlagen­forscher der Grafik­programmierung berühmt. Dl ist die Farbe des Lichts, Dm die Farbe der Oberfläche an der betrachteten Stelle. Diese Oberflächen­farbe kann aus einer Textur ausgelesen sein. Der Potenzwert n bestimmt die Größe der Glanzlichter. Größere Werte bedeuten kleinere Glanzlichter der spiegelnden Reflexion. Die vorkommenden Vektoren bezeichnen mit
• L: die einfallende Lichtrichtung, mit
• N: die Normale am Oberflächen­punkt und mit
• H: den so genannten Halfangle Vektor. Letzterer hängt auch von der Position des Punktes auf der Oberfläche und der Lichtquelle ab.

Wenn Sie sich obige Blinn-Formel genauer ansehen, fällt auf, dass es zwei Wege gibt, die Oberfläche nicht entsprechend der geometrischen Vorgaben, also nach dem Dreiecksnetz, darzustellen.
• Der erste Ansatzpunkt: Verschieben Sie die Punkte der Oberfläche. Diese Technik nennt sich Displacement-Mapping und funktioniert für heutige 3D-Hardware nicht in Echtzeit.
• Die zweite Variante, das Bumpmapping, setzt an der Oberflächen­normalen an.

Für ein 3D-Objekt verwenden Sie eine Textur, aus der die Farbwerte Dm für die Oberfläche gespeichert sind, und eine oder mehrere Bumpmaps, die die Perturbation (die Änderung der Oberflächen­normalen) enthält.

Mit den aktuellen 3D-Grafikkarten lässt sich die Beleuchtung für jeden gerenderten Pixel in Echtzeit berechnen.

Dot Product Bumpmapping

Für das Dot Product Bumpmapping Verfahren benötigen Sie moderne GPUs. Es basiert auf Bumpmaps, die als RGB-Texturen gespeichert werden. Die RGB-Werte eines Texels (zwischen 0 und 255) repräsentieren die x-, y- und z-Komponenten eines Vektors im Intervall [-1, 1]. Solche Bumpmaps können Sie sich aus Heightfields erzeugen lassen. Sie können ein Tool von nVidia (inklusive Sourcecode) downloaden, um RGB-Normal-Maps aus Heightfields zu generieren. Dieses Werkzeug finden Sie unter den Developer-Informationen auf der nVidia-Homepage zum freien Download: www.nvidia.com. Die Komponenten der Normalen­vektoren werden durch Ableiten des Heightfields berechnet. Die zentrale Operation bei der Beleuchtungs­berechnung des Bumpmappings und der diffusen Beleuchtung ist das Skalarprodukt aus der Normalen und des Vektors vom Oberflächen­punkt zur Lichtquelle:

N * L

Diese Formel entspricht dem Lambertschen Gesetz. Es ist egal, in welchem Koordinaten­raum die beiden Vektoren angegeben sind, es muss aber beides mal der selbe sein. Doch welcher Raum soll das sein und in welchem ist die Normale angegeben? Die Antwort darauf gibt das Tangent Space Bumpmapping.

Der entscheidende Koordinaten­raum ist der so genannte Tangent Space. Diesen drei­dimensionalen Raum geben Sie durch eine 3-x-3-Matrix an, deren drei Spalten­vektoren den Raum aufspannen. Sie benötigen für jeden Vertex Ihres 3D-Modells einen Tangent Space. Die Normale des 3D-Modells am Vertex wählen Sie als +z-Achse, also als dritten Spaltenvektor. Durch den Vertex und seine Normale ist eine Ebene definiert, die sich tangentiell zur Oberfläche befindet, daher der Name Tangent Space.

Sie brauchen noch zwei weitere Vektoren, um den Raum aufzuspannen. Wählen Sie zum Beispiel die +y-Achse des Modelspace (des Koordinaten­raumes, in dem Ihr 3D-Modell definiert wurde) oder einen Vektor, den Sie durch die implizite Beschreibung einer Oberfläche erhalten. Im Beispiel­programm finden Sie dafür einen Torus. Der noch fehlende dritte Vektor ergibt sich aus dem Kreuzprodukt der beiden anderen. Normalerweise werden die Vektoren so konstruiert, dass sie in der Tangential­ebene an der Oberfläche liegen.

Nun haben Sie zu jedem Vertex einen Tangent Space definiert, den Sie für das Rendern speichern müssen. Die folgenden Schritte müssen Sie während der Laufzeit des Programms erledigen. Interpretieren Sie Ihr Heightfield so, dass die Höhen­information eine Verschiebung entlang der +z-Achse des Tangent Space bewirkt. Sie transformieren den Vektor zur Lichtquelle in den Tangent Space: Wenn Sie Ihr 3D-Modell rendern, generieren Sie auf dem Matrix-Stack von OpenGL eine Reihe von Trans­formationen. Sie benötigen die inverse Transformation. Dazu invertieren Sie entweder die resultierende ModelView-Matrix, oder Sie erzeugen eine Matrix mit den einzelnen invertierten Transformations­schritten in umgekehrter Reihenfolge. Wenn Sie mit dieser inversen Matrix die Position der Lichtquelle in Ihrer 3D-Welt transformieren, erhalten Sie einen Ortsvektor, der die Position der Lichtquelle im Modelspace beschreibt.

Als letzten Schritt berechnen Sie den Vektor eines jeden Vertex zur Lichtquelle (in Modelspace-Koordinaten) durch Subtraktion und transformieren diesen Vektor L in den Tangent Space. Die Transformation in den Tangent Space erfolgt durch das Skalarprodukt aus dem L-Vektor und jedem der Spalten­vektoren.

Beim Rendern eines Dreiecks durch die 3D-Hardware werden die Normalen als RGB-Tripels behandelt und linear perspektivisch korrekt interpoliert. Die L-Vektoren können sich in unter­schiedlichen Tangent Spaces befinden, denn jeder Vertex des Dreiecks hat seinen eigenen Tangent Space. Die 3D-Hardware routiert gewissermaßen die L-Vektoren von einem Raum in den nächsten.

Eine mathematisch korrekte Beleuchtungs­berechnung müsste diese Vektoren für jeden Pixel normalisieren, da sich ihre Länge bei der linearen Interpolation der Vektor-Komponenten ändert.

Dafür bietet sich Cube Mapping an: Das ist eigentlich eine Form des Texture-Mapping, die einen unnormal­isierten Vektor verwendet, um eine Textur zu adressieren. Diese besteht aus sechs quadratischen 2D-Bitmaps, die wie die Flächen eines Würfels angeordnet sind. So sehen Sie, wie ein Vektor einen Pixel adressiert.

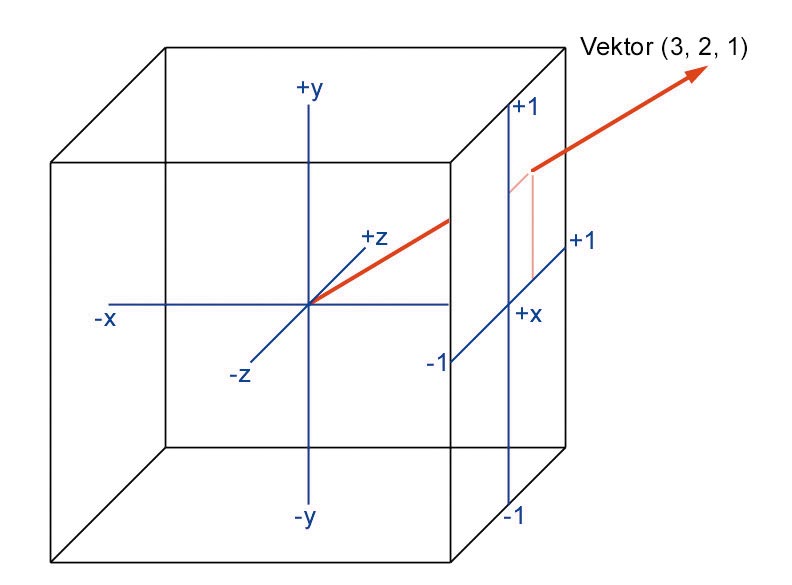
Die Komponente mit dem größten Betrag und ihr Vorzeichen bestimmen, welche Seite des Würfels getroffen wird. Die 2D-Koordinaten auf der Würfelseite erhalten Sie, indem Sie die beiden kleineren Komponenten durch die Größte dividieren. Ein RGB-Tripel, das durch die Interpolation der Normalen im Tangent Space entsteht, wird als Vektor interpretiert. Dieser Vektor schneidet den Würfel an einer bestimmten Stelle. Die Lage des Schnittpunkts ist unabhängig von der Länge des Vektors, nur die Richtung ist entscheidend.

Sie können die Cubemap-Texturen so vorberechnen, dass an jeder Stelle ein bestimmtes RGB-Tripel gespeichert ist: das RGB-Tripel, das dem normalisierten Vektor entspricht. Im übrigen werden Cubemaps dazu verwendet, Licht-Reflexionen oder -Refraktionen (Lichtbrechung) darzustellen.

Seit 1978 haben Entwickler daran gearbeitet, das von Blinn formulierte Bumpmapping in 3D-Hardware zu integrieren. In unserem Beispiel­programm finden Sie die Implementation und Fortführung der hier gezeigten Verfahren. Mit dieser Vorarbeit können Sie zur Ansteuerung der GeForce-Karte übergehen.

Register Combiners

GeForce-, Quadro- und neuere nVidia-Karten besitzen Register-Combiners. Damit lässt sich die Farbberechnung für jeden Pixel konfigurieren. Beachten Sie den Unterschied zwischen Konfigurieren und Programmieren: ersteres ist Einstellen, letzteres freies Gestalten. Dieses erlauben erst die Pixelshader der neuesten Karten­generationen. Die Register-Combiners ersetzen, wenn Sie sie aktivieren, die Standard-OpenGL-Rendering­optionen. Sie sind deutlich komplexer und flexibler. Die Register-Combiners steuern Sie über OpenGL Extensions. Diese sind in der neuesten Version der Datei glext.h definiert, die Sie auch bei unserem Beispiel­programm finden. Wie Sie die Funktionen nutzen, entnehmen Sie dem Beispiel­programm. Auf den Entwickler­seiten von nVidia finden Sie die genauen Spezifi­kationen und Dokumen­tationen aller Features.

Dot-3-Bumpmap-Texturen

Um eigene Bumpmaps für Dot-3-Bumpmapping zu generieren, beginnen Sie mit einem Heightfield, also einer Graustufen-Bitmap. Hellere Graustufen bedeuten, dass die so gekenn­zeichnete Oberfläche mehr nach außen geschoben wird. Eine solche Bumpmap-Textur wandeln Sie mit dem nVidia-Bumpmap-Tool in eine RGB-Normal Map um:

normalmapgen.exe height.tga bump.tga

Bevor Sie die Maps in OpenGL laden, generieren Sie Mipmaps. Das sind niedrigere Auflösungs­stufen einer Textur, um hässliche Effekte beim Rendern zu vermeiden. In der Textur befinden sich vorzeichen­behaftete Vektoren, die nur als RGB-Werte gespeichert sind. Das weiß die gluBuild2DMipmaps(...)-Funktion von OpenGL nicht, die automatisch Mipmaps generiert. Da diese für diesen Zweck unbrauchbar sind, müssen Sie eigene Mipmaps generieren, also eine Funktion implementieren, die die Auflösung einer RGB-Normalmap halbiert! Dazu speichern Sie jeden Pixel der RGB-Normal in folgender Struktur, die die Vektor-Komponenten und seine Länge enthält:

typedef struct
{
	unsigned char nz, ny, nx, mag;
} DOT3NORMAL;

DOT3NORMAL bumpmap[SIZE*SIZE];
		

nx, ny und nz initialisieren Sie jeweils mit den RGB-Werten, mag mit dem Wert 255. Bei der Halbierung der Auflösung fassen Sie vier benachbarte Pixel, die in einem Quadrat angeordnet sind, zu einem neuen zusammen. Die Komponenten der Vektoren a, b, c und d müssen Sie vom Wertebereich [0,255] auf der Intervallskala [-1,1] verschieben und skalieren. Die Werte innerhalb des Intervalls multiplizieren Sie mit der Länge des ursprünglichen Vektors und summieren sie auf. Damit erhalten Sie einen neuen Vektor, den Sie erneut normalisieren und als RGB-Tripel in der neuen Mipmap-Stufe speichern. Zusätzlich speichern Sie vorher seine Länge in mag. Der Code für einen Pixel sieht so aus:

//a,b,c,d: Texel in bumpmap[]
// angeordnet als
// a b
// c d
DOT3NORMAL a, b, c, d;
DOT3NORMAL neu;
VERTEX n;
n.x = (a.nx / 127 - 1) * a.mag / 255;
n.x += (b.nx / 127 - 1) * b.mag / 255;
n.x += (c.nx / 127 - 1) * c.mag / 255;
n.x += (d.nx / 127 - 1) * d.mag / 255;
...

l = lengthVector(n);
normVector(n);
neu.nx = 128 + 127 * n.x;
...

neu.mag = min(255, 255 * l * 0.25);
		

Die so berechneten Mipmap-Stufen übergeben Sie mit glTexImage2D(...) an OpenGL. Wenn Sie alles zusammenfassen und mit den Implementierungs­details ausstatten, erhalten Sie unser fertiges Dot-3-Bumpmapping-Programm.

Emboss-Bumpmapping

Nun gibt es noch ein sehr altes, anderes Verfahren, um Bumpmapping darzustellen. Das Emboss-Bumpmapping ist auf jeder 3D-Karte einsetzbar. Durch diesen Fakt ließen sich schon manche 3D-Karten­hersteller zur Behauptung verleiten, ihre 3D-Karten würden Bumpmapping in der Hardware unterstützen. Diese Methode ist mit den Embossfiltern in Bildbearbeitungs­programmen verwandt. In bestimmten Fällen sind beim Emboss-Bumpmapping Darstellungs­artefakte durch Unterabtastung zu sehen, die als unscharfe Bewegungen erscheinen. Wenn Sie unser Beispiel­programm dazu ausprobieren, werden Sie sehen, dass sich der Einsatz aber auf jeden Fall lohnen kann.

Das Verfahren lässt nur die Approximation der diffusen Beleuchtungs­komponente zu, womit sich die vorige Formel für die Beleuchtungs­berechnung auf folgende Terme reduziert:

C = ((L * N)) x Dl x Dm

Diese Formel hat gewaltig gegenüber der Blinn’schen-Ausgangsformel an Komplexität verloren: Es fehlen nicht nur die Rechen­operationen, sondern auch der Halfangle-Vektor, den Sie für das Dot-3-Bumpmapping benötigten. Die Bumpmap, die wir für das Emboss-Bumpmapping einsetzen, ist eine Höhen­information (Heightfield/Graustufen-Bitmap): Wie das erste Bild zeigte, repräsentiert ein Pixel in der Bumpmap eine Höhen­verschiebung auf der Oberfläche.

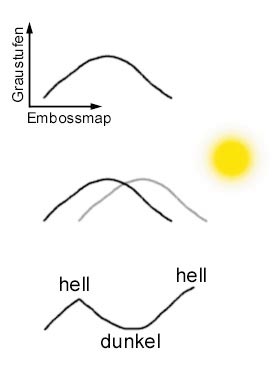
Wir betrachten das Verfahren zunächst im Ein­dimensionalen, also mit einer Zahlenreihe, die einen Höhenverlauf darstellt. Wenn Ihnen die erste Ableitung einer Folge von Höhenwerten vorliegt, entspricht diese der Steigung am entsprechenden Oberflächen­punkt. Diese Steigung m wird verwendet, um einen Basisfaktor Fd für die diffuse Beleuchtung zu erhöhen oder zu erniedrigen. Die Summe (Fd+m) approximiert den Term (L*N).

Als nächstes approximieren Sie die Steigung. Lesen Sie die Höhe H0 des Oberflächen­punktes aus der entsprechende Stelle der Heightmap, was später die 3D-Hardware für Sie erledigen wird. Lesen Sie die Höhe erneut aus, wobei Sie die Bumpmap ein kleines Stückchen in Richtung der Lichtquelle verschieben, und Sie erhalten H1. Rechnen Sie diese Verschiebung aus. Die Differenz aus H0 und H1 ergibt: m = H1 - H0.

Die Textur verschieben Sie, indem Sie die Textur­koordinaten modifizieren. Die Modifikation berechnen Sie wieder im Tangent Space. Dazu transformieren Sie die Lichtquelle in den Modelspace. Bilden Sie die Skalarprodukte des Vektors von einem Vertex zur Lichtquelle und der Tangente sowie der Binormalen des Tangent Space. Damit erhalten Sie zwei Verschiebung­swerte, die Sie zur ursprünglichen Texture-Koordinaten addieren.

Wenn Sie die Texturen und Bumpmaps in OpenGL geladen haben, führen Sie das Emboss-Bumpmapping in drei Renderpasses durch. Diese Variante funktioniert auf jeder OpenGL-Hardware, die Texture-Mapping unterstützt.
• Im ersten Renderpass verwenden Sie die Bumpmap-Textur mit den Original-Textur­koordinaten und deaktivieren die OpenGL-Beleuchtungs­berechnung und das Blending.

glBindTexture(GL_TEXTURE_2D, bumpTex);
glDisable(GL_BLEND);
glDisable(GL_LIGHTING);
renderObject();
		

• Im zweiten Schritt erhalten Sie die 3D-Objekte mit fertiger Beleuchtung, jedoch ohne Farbe. Dazu wählen Sie die invertierte Bumpmap-Texture, Blending mit GL_ONE/GL_ ONE und den berechneten verschobenen Textur­koordinaten:

glBindTexture(GL_TEXTURE_2D, invBumpTex);
glBlendFunc(GL_ONE, GL_ONE);
glDepthFunc(GL_LEQUAL);
glEnable(GL_BLEND);
renderObjectEmboss();
		

• Im dritten Renderpass kommt Farbe durch die Farbtextur und die OpenGL-Beleuchtung ins Spiel. Dazu verwenden Sie folgende Einstellungen:

glBindTexture(GL_TEXTURE_2D, textureMap);
glBlendFunc(GL_DST_COLOR, GL_SRC_COLOR);
glEnable(GL_LIGHTING);
renderObject();
		

Probieren Sie die High-End-Render­techniken aus. Wenn Sie Ihre 3D-Grafik mit den Bumpmapping-Features ausstatten, werden Sie feststellen, wie realistisch bisher flache, künstlich anmutende 3D-Objekte auf den Betrachter wirken können.

Um die mathematische Arbeit von James Blinn zu studieren, verweisen wir auf die nachfolgenden Literatur­angaben. Diese Grundlagen für die Berechnung von 3D-Räumen wurden erst in den letzten Jahren gelegt. Die komplexe mathematische Materie ist noch nicht vollständig erforscht.