Schnellster im Ziel

Carsten Dachsbacher

Lernen Sie den A*-Algorithmus (gesprochen: A-Stern) kennen. Dieser Algorithmus findet seit 1968 in der Künstlichen Intelligenz (KI) und in akademischen Suchsystemen Anwendung.

Der A*-Algorithmus löst die Grundaufgabe der meisten Computerspiele: Sie planen damit einen Pfad, auf dem sich eine Spielfigur in Computer­spielen bewegen soll. In der Spiele-KI neuerer Computerspiele, vor allem aus dem Echtzeit-Genre, tritt diese Situation häufig auf. Meist wird der Weg einer Figur berechnet, die sich auf einer Spielkarte zu einem vom Spieler gewählten Ziel bewegen soll.

Mit Hilfe des A*-Algorithmus können Sie Hindernissen ausweichen. Außerdem soll die Spielfigur die Gegebenheiten der Spielterrains bestmöglich ausnutzen. Der Spielheld soll also einen schlammigen Sumpf oder einen steilen Berg vermeiden und lieber auf Straßen oder freiem Gelände laufen.

Grundlagen: das Zahlenschiebepuzzle

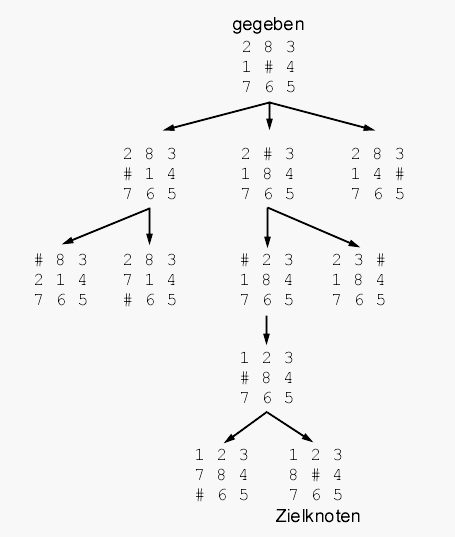
Der A*-Algorithmus ist ein Graph-Such­algorithmus. Ein Graph besteht aus Knoten, die durch Kanten verbunden sind. Dieser Graph ist implizit definiert, wie im Folgenden erklärt: Zu einem Knoten sind die Knoten angegeben, die durch Kanten direkt erreichbar sind. Eine explizite Definition würde die Adjazenz­information (die Verbindungs­information) von jedem Knoten zu jedem anderen speichern. Ein Knoten dieses Graphs entspricht einem Zustand in unserer A*-Suche. Was Sie suchen, spielt keine Rolle. Es geht nur darum, einen Lösungsweg darzustellen. Der A*-Algorithmus sucht für Sie den besten Pfad von einem gegebenen Start- zu einem gewünschten Endzustand. Dabei läuft er durch den Graphen und untersucht die Nachbarknoten der besuchten Zustände.

Ein bekanntes Spiel – und gern vorgeführtes Beispiel für den A*-Algorithmus – ist das 8er Zahlen­schiebepuzzle. Dieses bringt in einem 3 x 3 Feld die Ziffern 1 bis 8 unter. Die Ziffern können Sie verschieben. Der Graph erreicht einen neuen Zustand, wenn Sie eine Ziffer verschieben. Diesen Lösungsweg des Zustands­graphen zeigt das Bild unten.

Mit dem A*-Algorithmus können Sie auch den Pfad einer Spielfigur in einer virtuellen Welt planen. Der aktuelle Zustand entspricht in diesem Fall der momentanen Position der Spielfigur. Erreichbare Zustände entsprechen in diesem Beispiel Spielfeldern, die die Figur durch einen Bewegungszug erreichen kann.

Der A*-Algorithmus untersucht immer wieder den Zustand, der voraus­sichtlich zum optimalen Pfad gehört. Der Algorithmus untersucht dazu die Knoten des Graphen, die er noch nicht erforscht hat. Zuerst überprüft er, ob es sich schon um das Ziel handelt. In diesem Fall ist die Suche beendet. Sonst notiert der A*-Algorithmus alle Nachbar­zustände des gerade untersuchten Zustands, um sie später zu betrachten.

Der A*-Algorithmus speichert zwei Listen von Zuständen: die Open- und die Closed-Liste für unerforschte und erforschte Zustände. Zu Beginn der Suche ist die Closed-Liste leer. Die Open-Liste enthält nur einen Startzustand: die aktuelle Position der Spielfigur. Der A*-Algorithmus sucht sich wiederum den besten Zustand aus der Open-Liste, um ihn zu untersuchen und entfernt ihn daraus. Danach werden alle Nachbar­zustände erzeugt. Nun müssen Sie unterscheiden: Sind diese Zustände neu, werden sie an die Open-Liste angehängt.

Schnellster Weg aus dem Labyrinth

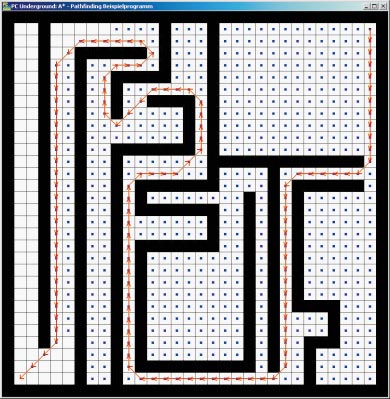
Befinden sich Zustände schon in der Open-Liste, dann wird – falls ein besserer Weg gefunden wurde – die Information dort neu gespeichert. Zustände in der Close-Liste für die der Algorithmus einen besseren Weg findet, nimmt er aus dieser Liste und fügt sie neu in die Open-Liste ein. Denn das könnte einen besseren Weg eröffnen. Das Suchen und Eintragen der Nachbar­zustände heißt Expansion eines Knotens. Wenn die Open-Liste leer ist, bevor der Endzustand erreicht wird, gibt es keinen Pfad vom Start- zum Endzustand.

Um den besten Zustand zu wählen, betrachten Sie zunächst die Struktur, um einen Zustand zu speichern:

class Position
{
private:
	int _x, _y;
	Position neighbour(const int d);
...
};

class Node
{
friend class AStar;
private:
	int g, h, f;
	Node *pred;
	int nPred;
	Position p;
...
};
		

Die Klasse Position, verwenden Sie, um einfacher 2D-Integer-Koordinaten zu speichern. Die Klasse bietet neben Zugriffs­methoden so genannte überladene Operatoren, um den Umgang mit Koordinaten zu erleichtern. Die Methode

Position::Position neighbour(const int d)

liefert die Position eines Nachbarknotens.

In der Node-Klasse speichern Sie die Daten eines Zustandes. Die Klasse enthält die aufsummierten Kosten des besten Wegs vom Startzustand bis zum aktuellen Knoten g und die geschätzten Restkosten zum Ziel h.

Weiterhin speichern Sie f, die Summe aus g und h, einen Zeiger auf den Vorgänger-Zustand und einen weiteren Zeiger auf der verketten Liste der Zustände *pred. Sie schreiben auch die Zahl der Vorgänger nPred und die Position des Knotens in der virtuellen Welt p in den Arbeits­speicher. Die Kosten bezeichnen damit den Aufwand, den die Spielfigur hätte, wenn sie den betrachteten Weg gehen würde. In einem Knoten sind in g die Kosten des optimalen Pfads vom Startzustand zu diesem Knoten gespeichert. Dieser Pfad ist nPred Knoten lang. Sie könnten ihn jederzeit zurück­verfolgen, indem Sie den *pred-Zeigern folgen.

Nun gilt es, die Kosten zu berechnen oder zu schätzen. Die Kosten vom Startzustand bis zum aktuellen Knoten können Sie exakt berechnen. Sie benötigen dazu nur eine Funktion, die Ihnen die Kosten liefert, wenn Sie Ihre Spielfigur von einem Feld zum nächsten bewegen würden. Die Restkosten h müssen Sie schätzen.

Den restlichen Weg haben Sie noch nicht untersucht. Den wollen Sie ja erst berechnen. Der A*-Algorithmus verlangt eine optimistische Restkosten­schätzung. Das bedeutet: Sie müssen die Restkosten schätzen, der Schätzwert muss kleiner sein, als die tatsächlichen Kosten sind. Trivial ist diese Bedingung erfüllt, wenn Sie die Restkosten immer auf 0 schätzen.

Der folgende theoretische Ansatz ist zwar in den Eigenschaften des A*-Algorithmus bewiesen, findet im Rahmen unserer Anwendung hier jedoch nur eine Randnotiz: Wenn es einen Pfad vom Start- zum Endknoten gibt, dann findet der A*-Algorithmus diesen, selbst wenn es sich um so genannte unendliche Graphen handelt. Unendliche Graphen sind bei impliziter Darstellung durchaus denkbar. In nicht-unendlichen Graphen terminiert der Algorithmus, wenn es keinen Pfad gibt.

Die Monotonie-Bedingung verlangt, dass die Differenz der Restkosten-Schätzwerte zweier Knoten kleiner ist als die tatsächlichen Kosten der Pfade zwischen den beiden Knoten. Ist diese Bedingung erfüllt, hat der Algorithmus zu jedem Knoten, den er zur Expansion wählt, bereits einen optimalen Pfad gefunden. Wenn Sie zwei A*-Algorithmen A1 und A2 mit den Restkosten­schätzungen c1(x) und c2(x) verwenden und c(x) die tatsächlichen Restkosten bezeichnet, gilt für jeden Zustand x :

c1(x) < c2(x) < c(x)

Für diese Bedingung gilt, dass A2 besser als A1 informiert ist. Das hat zur Folge, dass nach der Terminierung jeder Knoten, der von A2 expandiert wurde, auch von A1 expandiert wurde. A1 hat also mindestens so viele Knoten wie A2 expandiert. Es ist wichtig, die Zahl der Knoten und die Rechenzeit zu reduzieren.

Die Implementation des A*-Algorithmus

Nachdem Sie die Grundlagen des A*-Algorithmus kennen gelernt haben, wagen Sie sich an die Implementation heran. Wir stellen Ihnen hier eine Basis­implementation vor, die leicht verständlich, aber nicht rechenzeit­optimiert ist. Bei Punkten, an denen Sie eine Optimierung vornehmen können, weisen wir Sie an der entsprechenden Stelle darauf hin. Im Folgenden behandeln wir den Spezialfall, dass wir einen Pfad auf einer Spielwelt suchen, deren Karte aus einem regelmäßigen Schachbrett besteht. In einer Landkarte der Spielewelt speichern Sie, wie aufwendig es für die Spielfigur ist, sich darüber zu bewegen.

Die Implementation ist in der AStar-Klasse verpackt.

class AStar
{
private:
	Position start, goal;

	int lowestOpen;
	int lowestCost;
	int nodesExpanded;

	int nOpen, nClosed;
	Node **open;
	Node **closed;

	Node *goalNode;
		

Die Member-Variablen der Klassen speichern außer dem Start- und Zielpunkt die Open- und Closed-Listen als Array. In einer optimierten A*-Suche würden Sie diese als Priority Queues speichern. In Priority Queues, die Sie als binäre Bäume verwalten, geht es schneller, nach der Node (Knoten) mit den geringsten Kosten zu suchen. Außerdem speichern Sie den Index des voraus­sichtlich besten Knotens, seine Kosten und einen Zeiger auf den Endknoten, sofern dieser gefunden wurde.

Für die Verwaltung der Open- und Close-Liste benötigen Sie Methoden, um Elemente einzufügen, zu suchen oder zu löschen:

void pushNode(Node **list,
	int *count, Node *node)
{
	list[(*count)++] = node;
}

int containsNode(Node **list,
	int count, Node *me)
{
	for(int i = 0; i < count; i++)
		if(list[i]->p == me->p)
			return i;
	return -1;
}

void removeNode(Node **list,
	int *count, int me)
{
	list[me] = list[--(*count)];
}
		

Für die Kosten­berechnung oder -schätzung benötigen Sie folgende Funktionen, wobei Sie die Schätzung genauer untersuchen:

// Kosten als Integerwerte !
#define COSTDIAGONAL 554
// sqrt(2) * 100000 / 255
#define COSTSTRAIGHT 392
// 100000 / 255
static const int travCost[8] =
{
	COSTDIAGONAL, COSTSTRAIGHT,
	COSTDIAGONAL, COSTSTRAIGHT,
	COSTSTRAIGHT, COSTDIAGONAL,
	COSTSTRAIGHT, COSTDIAGONAL
};

// Berechnung: d ist eine der 8
// Richtungen auf der Karte
// (NW,N,NO,W,O,SW,S,SO)

int traversalCost(Position &a,
	Position &b, int d)
{
	int c = (map[a.x()][a.y()] +
		map[b.x()][b.y()]) >> 1;
	return c * travCost[d];
}

// Schätzung
int pathCostEstimate
	(Position &s, Position &g)
{
	return 0;
}
		

Beim Start der Suche löschen Sie die Open- und Close-Liste und erzeugen einen Startknoten, den Sie in die Open-Liste eintragen. Außerdem speichern Sie den Zielknoten:

void init(Position &s, Position &g)
{
	nOpen = nClosed = 0;
	Node *startNode = new Node();
	startNode->p = s;
	startNode->h =
	pathCostEstimate(s, g);
	startNode->f = startNode->h;
	startNode->pred = NULL;
	startNode->nPred = 0;
	goal = g;
	pushNode(open,&nOpen,startNode);
	lowestOpen = nOpen - 1;
	lowestCost = startNode->f;
}
		

Nun können Sie mit der Suche und der Expansion der Knoten anfangen:

int searchPath()
{
	//noch nodes in der open list?
	while(nOpen > 0)
	{
		// beste node nehmen
		Node *node = open[lowestOpen];
		removeNode((Node**)open,
			&nOpen, lowestOpen);
		findLowestCost();
		if (node->p == goal)
		{
			// ziel gefunden !
			goalNode = node;
			return node->nPred + 1;
		} else
		{
			expandNode(node);
			nodesExpanded ++;
		}
		pushNode(closed,&nClosed,node);
	}
	// kein weg gefunden !
	return -1;
}
		

Die Expansion der Knoten ist das Kernstück des A*-Algorithmus. Zunächst betrachten Sie jeden Nachbarknoten, der auf der Karte liegt und kein unbegehbares Spielfeld ist. Sie testen die Begehbarkeit in der If-Abfrage von isValid():

void expandNode(Node *node)
{
	for (int d = 0; d < 8; d++)
{
	Position p = node->p.neighbour(d);
	if (isValid(p))
	{
		

Die Kosten bis zu dieser Node können Sie berechnen und in einer neuen Node speichern:

int newCost = node->g +
	traversalCost(node->p, p, d);

Node *newNode = new Node(newCost,
	pathCostEstimate(p, goal),
	node, node->nPred + 1, p);

int io, ic, contained = 0, oldCost = -1;
		

Prüfen Sie, ob die neue Node schon in einer Liste gespeichert ist:

io = containsNode(open, nOpen, newNode);
ic = containsNode(closed, nClosed, newNode);

if (io != -1 || ic != -1)
{
	if (io != -1)
		oldCost = open[io]->g;
	else
		oldCost = closed[ic]->g;
}

if (oldCost != -1 &&
	oldCost <= newCost)
{
	delete newNode;
	continue;
}
else {
		

Nur einen neuen, besseren Weg zur aktuellen Node müssen Sie speichern:

	if (ic != -1)
		removeNode(closed,&nClosed,ic);

	if (io != -1)
		removeNode(open, &nOpen, io);

	pushNode(open,&nOpen,newNode);
	findLowestCost();
}
		

Wenn ein Weg gefunden ist, übertragen Sie diesen in ein Array aus der Elementen-Position. Dazu müssen Sie rückwärts den Weg vom Zielknoten aus verfolgen:

int getPath(Position *p)
{
	Position *dst=
		&p[goalNode->nPred];

	int length = goalNode->nPred + 1;
	Node *node = goalNode;
	while(1)
	{
		*dst = node->p;
		*dst--;
		if(node->pred != NULL)
			node = node->pred;
		else
			break;
	}
	return length;
}
		

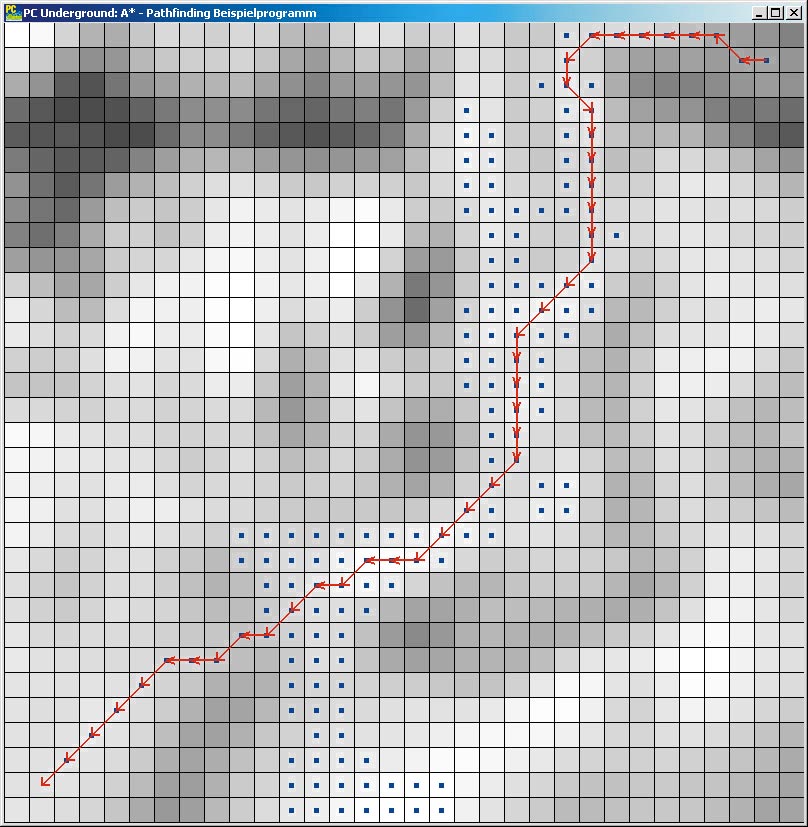
Im Bild oben sehen Sie die Landkarte aus dem Testprogramm der Heft-CD. Helle Felder sind leichter passierbar, dunkle schwerer und schwarze Felder gar nicht. Die roten Pfeile markieren den Weg der Spielfigur. Die Felder, deren Nodes expandiert wurden, sind mit einem kleinen blauen Kästchen gekennzeichnet.

Nachbarzustände

Nach der Theorie und der Implementation des A*-Algorithmus können Sie die Ästhetik und die Performance der Wegsuche verbessern.

Eine Karte aus regelmäßigen Feldern erleichtert die Wahl der Nachfolge­knoten, die aus den vier direkt anliegenden Nachbarfeldern und den vier diagonal erreichbaren Feldern resultieren. Wenn Sie die Pfadsuche daran hindern wollen, ein Feld zu betreten, schließen Sie dies in der Funktion expandNode(...) aus.

In Computer­spielen sichert dieses Verfahren, dass kein Fahrzeug über Wasser fährt und kein Schiff das Wasser verlässt. Wenn Sie einen beliebigen Graphen verwenden und kein regelmäßiges Gitter, ist es für die Rechenzeit wichtig, dass Sie die Adjazenz­information (Nachbarschaft- oder Verbindungs­information) für jeden Knoten speichern, denn Rechnen kostet Zeit und Geld.

Die Kostenfunktion

Die Kostenfunktion repräsentiert für einen Pfad vom Start- zum Endknoten den Wert, der minimiert werden soll. Das kann die Entfernung, Reisezeit oder verbrauchter Treibstoff sein. Sie können auch andere Faktoren einbringen. Denkbar wären Aufschläge für schlecht passierbares Terrain.

Je nach Typ der Spielfigur (Aktortyp) in Ihrem Spiel sollten Sie die Aufschläge variieren. Fahrzeuge bewegen sich auf Straßen deutlich schneller als querbeet, wohingegen der Unterschied für Infantrie nicht entscheidend ist. Die Kosten können von der Bewegungs­richtung abhängen. Bergauf ist teurer als bergab. Mit der Kostenfunktion beeinflussen Sie also nicht nur die Rechenzeit, sondern auch die Ästhetik des gefundenen Pfades und den Realismus. Die folgende einfache Kostenfunktion berücksichtigt die Richtung der Bewegung nicht, dafür das Terrain mit Start- und Endposition:

int traversalCost(Position &a,
	Position &b, int d)
{
	int c =(map[a.x()][a.y()] +
		map[b.x()][b.y()]) >> 1;

	return c * travCost[d];
}
		

Die Kostenschätzung

Die Schätzung der Restkosten ist ein weiterer zeitkritischer Punkt bei der Pfadsuche mit dem A*-Algorithmus. Die Restkosten optimistisch auf Null zu schätzen, ist an hier optimal: Die Rechenzeit ist auch Null.

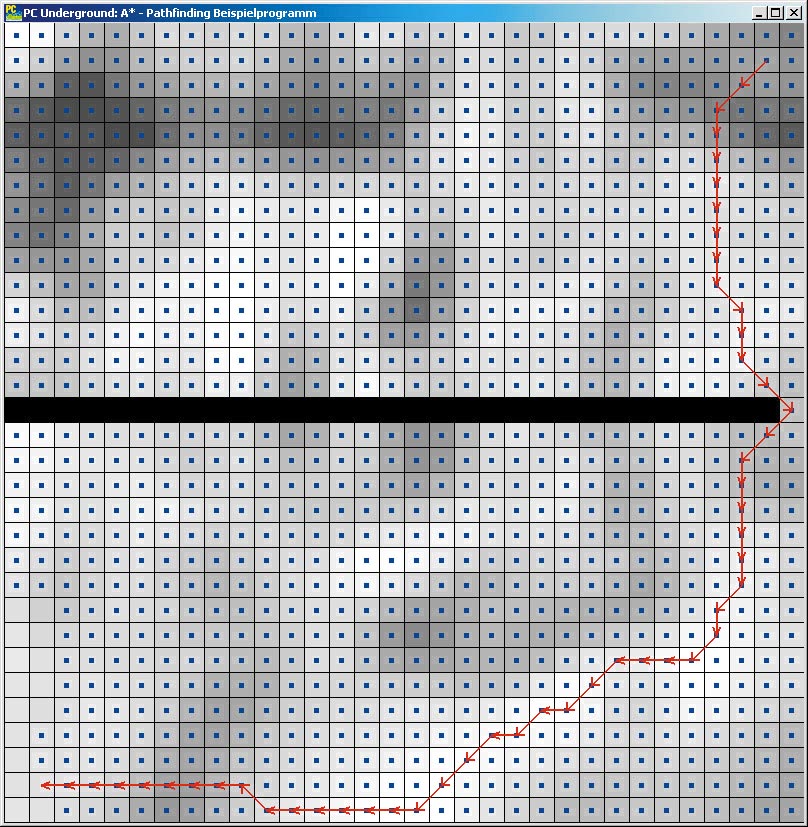
In Folge müssen Sie dafür sehr viel mehr Knoten expandieren als bei einer etwas sinnvolleren Schätzung: Verwenden Sie besser den euklidischen Abstand, den sie mit den minimalen Bewegungs­kosten multiplizieren. Diese Schätzung liefert schon deutlich bessere Ergebnisse.

Da der Abstand nicht kürzer sein kann als die Fluglinie, ist das auch eine optimistische Schätzung. Eine einfache Kostenschätz­funktion ist der euklidische Abstand zweier Knoten unter Berücksichtung der Begehbarkeit der Landschaft:

int pathCostEstimate(Position &s, Position &g)
{
	int c = (map[s.x() ][s.y()] +
		map[g.x()][g.y()]) >> 1;

	return max(abs(s.x()- g.x()),
		abs(s.y() - g.y())) *
		COSTSTRAIGHT * c;

	// triviale variante
	return 0;
}
		

Anhand der Zahl der expandierten Knoten in den beiden vorigen Bildern sehen Sie die Auswirkungen verschiedener Kosten­schätzungen. Diese beweisen, wie unter­schiedlich die Zahl der expandierten Knoten sein kann.

Schwächen des A*-Algorithmus

Der A*-Algorithmus kann auf großen Spielkarten sehr viel Speicher verbrauchen, wenn Hunderte oder Tausende von Nodes expandiert werden. Er nimmt die CPU stark in Beschlag.

Besonders schlecht ist der A*-Algorithmus in Fällen, in denen kein Weg existiert, da er dann jede vom Startknoten aus erreichbare Position expandiert. Um in diesem Fall Rechenzeit zu sparen, analysieren Sie vorab Ihre Spielfeldkarte. Dies können Sie manuell oder algorithmisch tun. Speichern Sie das Ergebnis, wenn es überhaupt einen Pfad zwischen zwei Feldern gibt.

Daneben gibt es einige Ansatzpunkte den A*-Algorithmus schneller zu machen. Sie können die Geschwindig­keit durch bessere Expansion der Knoten und der Restkosten­schätzung erhöhen. Die Ästhetik können Sie durch Ausschließen von Knoten, die Glättung des resultierenden Pfades oder Verwendung von Splines für die tatsächlichen Wege verbessern.