Schnell und schön

Carsten Dachsbacher

Mit dem A*-Algorithmus programmieren Sie für Ihre Spielhelden einen sicheren Weg selbst durch sumpfiges Gelände. In PC Underground 8/01 (ab S. 216) kam die Basis-Implementation zum Einsatz. In dieser Ausgabe programmieren Sie eine optimierte Variante mit weiteren Algorithmen. Der Blick auf die Ästhetik der A*-Pfade dient keiner philoso­phischen Betrachtung über Wahrheit, sondern beschreibt pragmatisch: Der schönste Weg ist auch der schnellste.

Mit dem A*-Algorithmus können Sie zwar einen beliebigen Pfad für eine Spielfigur berechnen. Doch das reicht nicht: Der Pfad soll den Eindruck vermitteln, dass er von einem Lebewesen gewählt wurde. Er muss drei Kriterien erfüllen:
• Er soll gerade werden, also seine Richtung so wenig wie möglich ändern.
• Er soll mehr abgerundet als zackig verlaufen.
• Er soll möglichst direkt verlaufen.

Gerade Pfade

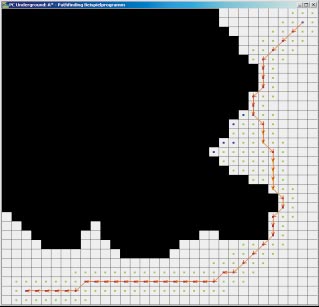
Die Pfade, die ein A*-Algorithmus berechnet, weisen oft unnötige Richtungs­änderungen auf (siehe Bild rechts oben).

Es gibt zwei Ansatzpunkte, um Pfade zu begradigen:
• Die erste Methode verursacht eine Richtungs­änderung zusätzliche Rechenzeit (auch Kosten genannt), so dass der A*-Algorithmus gerade Pfade bevorzugt.
• Die andere Variante versucht, den resultierenden Pfad des A*-Algorithmus zu begradigen.

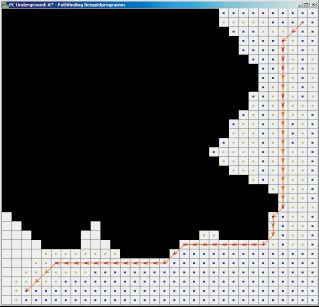
Es kommt vor, dass zwei Pfade die gleiche Rechenzeit benötigen, aber einer realistisch wirkt und der andere eine betrunkene Spielfigur vermuten lässt. Der A*-Algorithmus kann das nicht unterscheiden und liefert den Pfad als Ergebnis, den er als erstes findet. Um den A*-Algorithmus auf dem geraden Pfad zu halten, erhöhen Sie den Wert der Kostenfunktion bei einer Richtungs­änderung und führen damit Strafkosten für Richtungs­änderungen ein. Diese Modifikation berücksichtigt nur den Übergang von einem Feld zum nächsten. Als Startwert für Experimente mit Strafkosten wählen Sie zum Beispiel die halben Kosten einer normalen Bewegung.

In die expandNode(...)-Funktion unserer A*-Implementation fügen Sie dazu Folgendes ein:

...
// 8-Bewegungsrichtungen
// S, SO, O, SO, N, NW, W, SW
static const int xofs[8] =
	{ 0, 1, 1, 1, 0, -1, -1, -1 };
static const int yofs[8] =
	{ -1, -1, 0, 1, 1, 1, 0, -1 };

// Tabelle mit Strafkosten
int costModify[] =
{
	0, COSTSTRAIGHT * 128, COSTSTRAIGHT * 256,
	0x7fffff, 0x7fffff, 0x7fffff,
	0x7fffff, 0x7fffff
};

// liefert Bewegunsrichtung
int getDirIndex(int dx, int dy)
{
	for(int dir = 0; dir < 8; dir++)
		if(xofs[dir] == dx &&
			yofs[dir] == dy)
				return dir;
}

if (isValid(p))
{
	// Strafkosten
	travCostModify = 0;

	// Vorgänger vorhanden ?
if (node->pred)
{
	// vorherige Richtung
	dirX = p.x() - node->p.x();
	dirY = p.y() - node->p.y();
	dir = getDirIndex(dirX, dirY);
	// neue Richtung
	lastDirX = node->p.x();
	node->pred->p.x();
	lastDirY = node->p.y();
	node->pred->p.x();
	lastDir = getDirIndex(lastDirX, lastDirY);

	// Abweichung der neuen und alten Richtung
	int rot = lastDir - dir;
	if(rot > 4) rot = 8 - rot;
	if(rot < -4) rot = 8 + rot;
	rot = abs(rot);
	travCostModify = costModify[rot];
}
...
		

Wenn Sie Strafkosten verteilen, dauert die Berechnung für die Pfadsuche entsprechend länger. Der Algorithmus muss mehr Pfade betrachten, um sich für den besten entscheiden zu können.

Flüssige Bewegungen

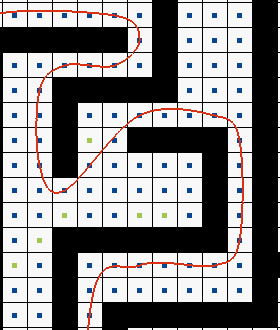
Selbst wenn Sie die Pfade des A*-Algorithmus begradigt haben, so sind die noch verbleibenden Richtungs­änderungen immer noch abrupt (in einem Winkel von mindestens 45 Grad). Die Lösung kommt aus der Computergrafik: Der berechnete Pfad ist eine Folge von Punkten. Diese Punkte können Sie als Stützpunkte einer parametrischen Kurve (etwa einer Bézier-Kurve) ansehen. Bézier-Kurven verlaufen nur durch den ersten und den letzten Stützpunkt. Da der A*-Algorithmus Hindernisse auf der Spielkarte umlaufen soll, muss sich die Kurve aber möglichst genau am gefundenen Pfad orientieren. Mit den Catmull Rom Splines berechnen Sie einen abgerundeten Pfad (vgl. Bild unten).

Übergeben Sie der Catmull Rom-Formel vier Stützpunkte. Mit einem Parameter u, der im Intervall von 0 und 1 verläuft, erhalten Sie eine glatte Kurve zwischen dem zweiten und dritten Punkt:

out = p1 * (-0.5f * u * u * u +
	u * u - 0.5f * u) +
	p2 * (1.5f * u * u * u -
	2.5f * u * u +1.0f) +
	p3 * (-1.5f * u * u * u +
	2.0f * u * u + 0.5f * u) +
	p4 * (-0.5f * u * u * u -
	0.5f * u * u);
		

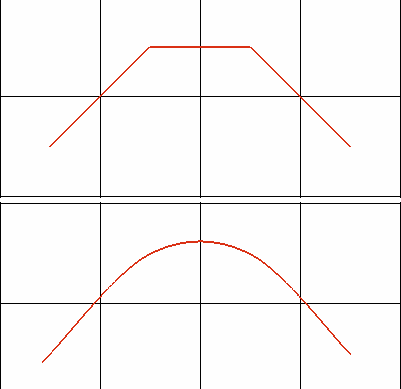
Wenn u gleich 0 ist, erhalten Sie als Ergebnis den Punkt p2, für den Wert 1 erhalten Sie p4. Für das erste und das letzte Kurvensegment Ihres A*-Pfads übergeben Sie den ersten bzw. den letzten Stützpunkt des Pfades doppelt. Folgender Code-Ausschnitt zeigt das Zeichnen des Spline-Pfads:

void interpolatedPosition(float *x, float *y,
	Position *a, Position *b,
	Position *c, Position *d,
	float u)
{
	u3 = u * u * u;
	u2 = u * u;
	f1 = -0.5f * u3 +u2 - 0.5f * u;
	f2 = 1.5f * u3 -2.5f * u2 + 1.0f;
	f3 = -1.5f * u3 + 2.0f * u2 + 0.5f * u;
	f4 = 0.5f * u3 - 0.5f * u2;
	*x = a->x() * f1 + b->x() * f2 +
		c->x() * f3 + d->x() * f4;
	*y = a->y() * f1 + b->y() * f2 +
		c->y() * f3 + d->y() * f4;
}

void drawPathCatmullRom(Position
	*path, int length)
{
	glBegin(GL_LINE_STRIP);
	for (i = 0; i < length; i++)
	{
		for(float u = 0.0f; u < 1.0f; u += 0.01f)
		{
			float x, y;
			interpolatedPosition(
			&x, &y,
			&path[max(0, i - 1)],
			&path[i],
			&path[min(i + 1, length - 1)],
			&path[min(i + 2, length - 1)], u);
			glVertex2f(x + 0.5f, y + 0.5f);
		}
	}
}
		

Wenn die Rechenzeit bei der Spline-Interpolation eine Rolle spielt, genügt es auch, für verschiedene, vorher festgelegte u Werte die Faktoren f1, f2, f3 und f4 vorzuberechnen und den Pfad nur um eine begrenzte Anzahl von Zwischen­punkten zu ergänzen:

// u = 0.0
out = p2;
// u = 1.0/3.0
out = -0.0740740 * p1 +
	0.7777777 * p2 +
	0.3333333 * p3 -
	0.0370370 * p4;

// u = 2.0/3.0
out = -0.0370370 * p1 +
	0.3333333 * p2 +
	0.7777777 * p3 -
	0.0740740 * p4;

// u = 1.0
out = p3;
		

Den neuen Pfad mit den zusätzlichen Zwischen­punkten können Sie einfach für Ihre Spielfigur verwenden, indem Sie sie stückweise linear bewegen lassen. Die Anzahl der neuen Punkte ist bei der obigen Rechnung dreimal so hoch wie die des Ausgangspfads. An geraden Teilen des Pfads können Sie kollineare Punkte (die Punkte, die auf der Verbindungs­gerade des Vorgänger- und des Nachfolger­punktes liegen) wieder entfernen.

Hierarchischer A*-Algorithmus

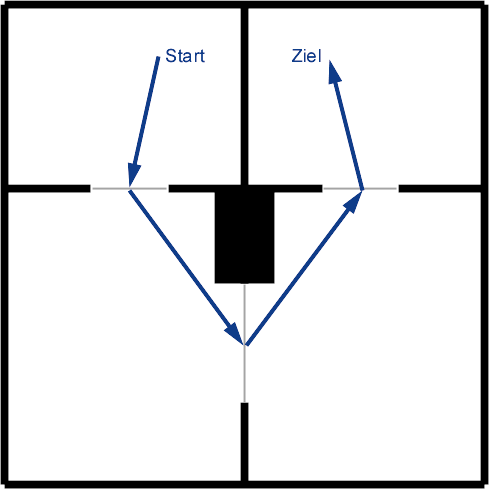
Stellen Sie sich ein Gebäude vor, in dem Sie mit dem A*-Algorithmus einen Pfad planen wollen. Außer der Karte, die ein Gebäude­geschoss in viele Quadrate aufteilt, können Sie einen Verbindungs­graphen aufbauen. Dazu speichern Sie, welcher Raum von welchem Raum jeweils durch eine Tür erreichbar ist. Der A*-Algorithmus kann jede Form von Graphen durchsuchen.

Die hierarchische Pfadsuche erfolgt in zwei Schritten:
• Im ersten Schritt planen Sie den Pfad grob,
• im zweiten Schritt berechnen Sie den Verlauf des Pfads im Detail.

Der erste Schritt besteht also darin, zu suchen, durch welche Räume des Gebäudes der Pfad führt. Im zweiten Schritt planen Sie dann auf dem Level der Spielfelder die Pfade innerhalb eines Raums zur Tür zum nächsten Raum.

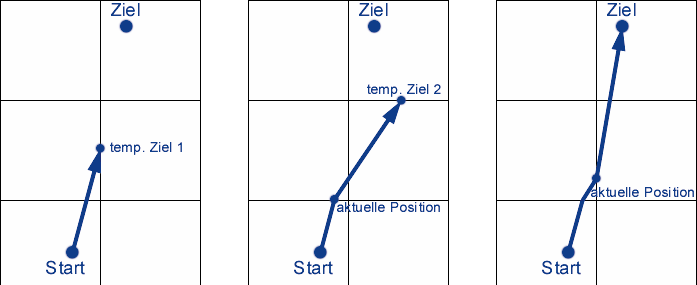
Mit der hierarchischen Pfadsuche sparen Sie sehr viel Rechenzeit, weil Sie den Suchraum (die Größe des Graphen, die der A*-Algorithmus durchsucht) drastisch reduzieren. Leider verläuft der Pfad wegen der Verbindungs­information der Räume immer durch die Mitte der Türen. Um den optimalen Pfad durch die Räume zu finden, müssen Sie mehr Rechenzeit investieren. In Verbindung mit der hierarchischen Pfadsuche können Sie sich das aber leisten: Suchen Sie auf der zweiten Ebene nicht den Pfad zur nächsten Tür, sondern zur übernächsten. Sie speichern aber nur den Teil des Pfads, der Sie zur nächsten Tür führt, und verwerfen den Rest.

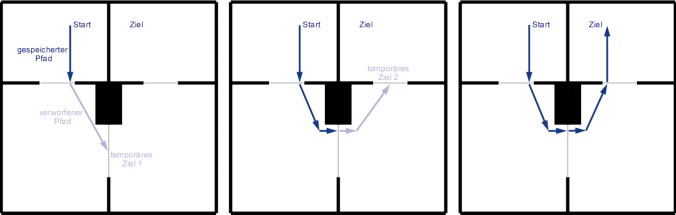
Die einzelnen Schritte:
• Suchen Sie den besten Pfad durch die Räume: 1, 2, 3, 4 • Suchen Sie den Pfad vom Start zum Punkt P2.
• Verwerfen Sie den zweiten Teil des Pfades.
• Suchen Sie den Pfad zum Punkt P3.
• Verwerfen Sie den zweiten Teil des Pfades.
• Suchen Sie den verbleibenden Pfad zum Ziel.

Die hierarchische Pfadsuche funktioniert genauso auf Spielwelten, die nicht aus Räumen bestehen, sondern aus einer Landkarte: Legen Sie einfach eine grobe Repräsentation Ihrer Karte an. Für eine Karte mit 256 x 256 Feldern berechnen Sie eine kleine Version mit 32 x 32 Feldern. Ein Feld auf der kleinen Karte steht für 8 x 8 Spielfelder. Für die hierarchische Pfadsuche ist es egal, ob Sie im ersten Schritt den Verbindungs­graph für Felder oder für Räume verwenden.

Rechenzeit-Optimierungen

Die benötigte Rechenzeit können Sie mit der hierarchischen Methode sowie mit der Kostenfunktion beeinflussen. Die Verkleinerung des Suchraums und die Kostenfunktion sind ein Ansatzpunkt der Optimierung. Weiterhin können Sie den Algorithmus sowie den Code verbessern. Dazu implementieren Sie eine Reihe von Funktionen und Klassen, die den A*-Algorithmus signifikant beschleunigen!

Pre-Allocating Memory

Der A*-Algorithmus untersucht Nodes (Knoten), die er zwischen­speichert. Statt jedes Mal neu Speicher für einen Node zu allokieren (adressieren), reservieren Sie von vornherein Speicher für genügend Nodes. Bei Bedarf nehmen Sie den Speicher aus der NodeBank. Eine einfache C++-Klasse hierfür sieht so aus:

class NodeBank
{
#define MAXBANKSIZE (256*256)
private:
	int n;
	Node *nodebank;

public:
	NodeBank(): n(0)
	{
		nodebank = new Node[MAXBANKSIZE];
	}

	~NodeBank()
	{
		delete nodebank;
	}

	Node *getNewNode()
	{
		if (n < MAXBANKSIZE)
			return &nodebank[n++];
		else
		{
			kein Speicher mehr !
			exit(1);
		}
	}
};
		

Die Master Node List

Ändern Sie die Architektur der A*-Speicher­strukturen. Bisher haben Sie eine Open- und eine Close-Liste gespeichert. Diese Methode ist sehr anschaulich, aber nicht optimal für die Rechenzeit. Fassen Sie diese beiden Listen zusammen. Um dennoch unterscheiden zu können, ob ein Node open oder closed ist, speichern Sie zwei Flags in der Node-Klasse. Hier sehen Sie die für A* relevanten Daten:

class Node
{
private:
	int g, f;
	Node *pred;
	Position p;
	bool inOpen,inClosed;
...
};
		

Diese Nodes speichern Sie in der Master-Node-List. Sie benötigen Funktionen, um einen Node anhand einer Position p zu suchen. Für eine schnelle Suche von Elementen in einer Liste eignet sich das Hashing. Dabei definieren Sie eine Hash-Funktion, die zu einer Position einen Hash-Wert berechnet:

#define HASHFUNC(p) {
	((p.x() & 255) << 8) |
	((p.y()) & 255)
}
		

Den Hash-Wert verwenden Sie als Index in einer Hash-Tabelle. An der Stelle zum Index speichern Sie den Node:

typedef struct HASHNODEPTR
{
	Node *node;
	HASHNODEPTR *next;
} HASHNODE;

HASHNODE *hash = new HASHNODE[MAXHASHSIZE];

...

// node in Hashtable speichern
int hashcode = HASHFUNC(node->p);
hash[hashcode]->node = node;
hash[hashcode]->next = NULL;
		

In der Hashnode-Struktur sehen Sie, dass außer dem Node noch ein Zeiger auf den nächsten Hashnode gespeichert wird. Der Grund: Es kann bei bestimmten Hash-Funktionen vorkommen, dass zwei unterschied­liche Positionen denselben Hash-Wert besitzen. In diesem Fall speichern Sie alle Nodes mit demselben Hash-Wert in einer verketteten Liste, die bei hash[ hashcode ] beginnt. Wenn Sie einen Node suchen, verwenden Sie folgende Funktion:

Node *getNodeStored(Position p)
{
	int hashcode = HASHFUNC(p);
	HASHNODE *node = &hash[hashcode];
while(node != NULL &&
	node->node != NULL &&
	node->node->p != p)
		node = node->next;

if (node != NULL)
	return
		node->node;
	else
		return NULL;
}
		

Das Hashing finden Sie in der Klasse MasterNodeList im Sourcecode zu dieser Ausgabe. Während der A*-Suche benötigen Sie Node-Strukturen für eine Position. Ist ein Node schon bekannt, brauchen Sie einen Zeiger auf ihn in der MasterNodeList. Wenn Sie diesen Node das erste Mal erreichen, müssen Sie einen neuen erzeugen. Dazu verwenden Sie eine Funktion der MasterNodeList:

Node *getNode(Position p)
{
	// Node schon in der Liste ?

	Node *node = this->getNodeStored(p);
	if(node)
		return(node);
	else
	{
		// nein => neue Node
		Node *newNode = nodeBank->getNewNode();
		newNode->p = p;
		newNode->inOpen = false;
		newNode->inClosed = false;
		// und speichern
		this->storeNode(newNode);
		return(newNode);
	}
}
		

Priority Queues

Sie speichern alle Nodes zusammen in der Master Node List und die Open-Liste aus Performance Gründen nochmals separat in einer Priority Queue. Der A*-Algorithmus wählt für seine Wegsuche und die Expansion der Nodes immer den Node, der voraus­sichtlich zum optimalen Pfad gehört. Das ist der Node in der Open-Liste mit den niedrigsten Gesamtkosten.

Die Open-Liste kann sehr groß werden, und eine Suche nach dem besten Node sehr aufwendig sein. Deshalb speichern Sie die Liste sortiert in einer Priority Queue. Dadurch, dass Sie die Sortierung beim Einfügen und Entfernen von Nodes aufrecht erhalten, reduzieren Sie den Suchaufwand deutlich. Die STL (Standard Template Library) bietet genügend Funktionalität, um die benötigten Funktionen zu implementieren. Es gibt keine verwendbare vordefinierte Priority Queue in STL, aber mit den Funktionen eines Binary Heap (binärer Speicherplatz) können Sie die anfallenden Aufgaben erledigen.

Hier sehen Sie einen kleinen Auszug aus dem Sourcecode, der zeigt, wie Sie Elemente einfügen, entfernen und sortieren:

class PriorityQueue
{
private:
	std::vector<Node*> heap;
public:
	Node *pop() // O(log n)
	{
		// 1.Node niedrigsten Kosten
		Node *node = this->heap.front();
		// 1.node zum ende (N) bewegen
		// sortieren 1 bis N-1 neu
		std::pop_heap(this->heap.begin(),
			this->heap.end(),
			NodeCompare());
		// letzte Node wegnehmen
		//Heap ist wieder sortiert
		this->heap.pop_back();
		return(node);
}

void push(Node* node)
// O(log n)
{
	// Node am Ende speichern
	// => Heap ist unsortiert !
	this->heap.push_back(node);
	// Element einsortieren !
	std::push_heap(this->heap.begin(),
		this->heap.end(),
		NodeCompare());
}
...
};
		

Die std::push_heap(...)-Funktion sortiert den Heap neu. Dazu benötigt sie eine Vergleichs­funktion. Diese vergleicht die Gesamtkosten zweier Nodes. Geben Sie für STL in einer Klasse Folgendes an:

class NodeCompare
{
public:
	bool operator()(Node *a, Node *b) const
	{
		return(a->f > b->f);
	}
};
		

Fassen Sie die optimierten Routinen in der A*-Klasse – die Sie im PC-Underground-Beitrag Ausgabe 8/01 S. 216 implementiert haben – zusammen. Damit erhalten Sie eine optimierte Variante, um schnell den passenden Pfad zu suchen. Die zwei modifizierten Funktionen finden Sie im Listing expandnode.

Damit haben Sie alles eingebaut, was Sie für eine A*-Pfadsuche in einem Computerspiel benötigen. Wichtig ist noch, die Pfade rechtzeitig zu berechnen. In einem Computerspiel muss der Spieler sofort eine Reaktion einer Spielfigur feststellen, wenn er einen Befehl erteilt. Manchmal wird die benötigte Zeit für die Wegsuche mit einem Soundeffekt als Befehls­bestätigung kaschiert. Gleichzeitig müssen Sie in einem Computerspiel darauf achten, dass Sie nicht zu viel zusammen­hängende Rechenzeit bei der Wegsuche verbrauchen, da sonst das Spiel kurze Zeit still steht. Sie organisieren dazu die Berechnung und teilen sie auf. In den folgenden Literatur­angaben finden Sie interessante empfehlens­werte Links, die nicht mit weiter­führenden Informationen sparen.