Grafikzauber in 3D

Carsten Dachsbacher

Um effektvolle Routinen zu programmieren, brauchen Sie neben der Idee die richtigen Daten. Wichtig für eine ansprechende Darstellung sind die Texturen, die Sie den 3D-Objekten zuweisen.

Texturen sind Bilder oder Bitmaps, die Sie auf Polygone kleben. Texturen können neben Farb­informationen einen Alphakanal enthalten. Dieser speichert für jeden Pixel der Textur (auch Texel genannt) einen Alphawert. Alphawerte verwenden Sie für Transparenz­effekte.

Beim hier gewählten Texturformat verfügen Sie für den Alpha-, Rot-, Grün- und Blauwert über je acht Bits. Die Farbwerte setzen sich durch additive Farbmischung zusammen. Ein Alphawert von 255 bedeutet, dass ein Pixel opak (undurchsichtig) ist, ein Wert von 0 zeigt Transparenz an.

Aus Heft 6/00, (ab S. 246) wissen Sie, wie man Texturen direkt aus bmp-Dateien liest. Um einen Alphakanal für die Textur anzulegen, laden Sie die Textur in ein vorgebenes Texturformat. Die Konstante, die dieses Texturformat, bezeichnet, lautet:

D3DX_SF_A8R8G8B8

Kürzen Sie dieses Format mit A8R8G8B8 oder ARGB ab. Es sollen je acht Bits für alle Kanäle und einen Alphakanal reserviert werden. Mit folgenden Zeilen laden Sie eine ARGB-Textur:

D3DX_SURFACEFORMAT sf = D3DX_SF_A8R8G8B8;
DWORD flags = D3DX_TEXTURE_NOMIPMAP;
LPDIRECTDRAWSURFACE7 pTex;
D3DXCreateTextureFromFile(D3DDevice,&flags,0,0,&sf,NULL,
	&pTex,NULL,file,D3DX_FT_POINT);
		

In der Textur steht außer dem Wert 255 für jeden Texel die Bitmap. Diese Texturen (Surfaces) bleiben im Speicher. Sie greifen darauf zu, um Inhalte zu ändern.

Dazu fordern Sie die Surface an und sperren sie für andere Prozesse. Die folgenden Routinen behandeln eine A8R8G8B8-Textur:

surface = ptex;
// Textur von oben ändern
DDSURFACEDESC2 ddsd;
ddsd.dwSize = sizeof(ddsd);
while(surface->Lock(NULL, &ddsd, 0, NULL ) == DDERR_WASSTILLDRAWING);
		

Die Lock-Funktion füllt beim Aufruf die DDSURFACEDE SC2-Struktur mit den Informationen über die Surfaces wie Breite, Höhe, Pitch und setzt einen Zeiger auf die Texturdaten. Die Anzahl der Bytes variiert von der Zahl der Pixel. Hier interessieren folgende Daten:

DWORD lPitch = ddsd.lPitch;
BYTE* pBytes = (BYTE*)ddsd.lpSurface;
// feste Werte für A8R8G8B8
DWORD dwAShiftR = 24;
DWORD dwAMask = 0xff000000;
		

Nun können Sie Texel für Texel das Bild durchgehen und die Alphawerte ändern:

// enthält neue Alphawerte
unsigned char *pdata;
...

for(DWORD y = 0; y < ddsd.dwHeight; y++ )
{
	DWORD* pDstData32 = (DWORD*)pBytes;
	for(DWORD x = 0; x < ddsd.dwWidth; x++)
	{
		DWORD da = (pdata[y * ddsd.dwWidth + x] << dwAShiftR) & dwAMask;
		pDstData32[x] &= (DWORD)(-1 ^ dwAMask);
		pDstData32[x] |= (DWORD)(da);
	}
	pBytes += ddsd.lPitch;
}
		

Nach allen Änderungen müssen Sie die Surface wieder freigeben, um damit weiter arbeiten zu können:

surface->Unlock(NULL);

Alpha-Blending

Nun liegt Ihnen eine Textur mit Alphawerten vor. Den Alphakanal verwenden Sie hauptsächlich dazu, Objekte transparent erscheinen zu lassen.

Hier ist die Textur der Kugel transparent über dem Hintergrund gezeichnet. Eine schwebende durchsichtige Kugeln über Wasser fasziniert den Betrachter. Dazu müssen Sie die Direct3D Renderstates mit folgenden Schritten anpassen:

// Textur wählen
D3DDevice->SetTexture(0, pTex);
// Alpha Blending aktivieren
D3DDevice->SetRenderState(D3DRENDERSTATE_ALPHABLENDENABLE, TRUE);
		

Mit folgender Zeile erscheinen die Farbwerte der Kugeln in voller Intensität:

D3DDevice->SetRenderState(D3DRENDERSTATE_SRCBLEND, D3DBLEND_ONE);
		

Dazu addieren Sie die Farbwerte des Hintergrunds, die Sie zuvor mit dem umgekehrten Alphawert der Textur (255 minus Alphawert) multiplizieren:

D3DDevice->SetRenderState(D3DRENDERSTATE_DESTBLEND, D3DBLEND_INVSRCALPHA);
		

Stellen Sie das Beispiel wie im Bild auf Seite 256 transparent dar:
• Für das additive Shading genügt es, die Farb­intensitäten zu addieren:

D3DDevice->SetRenderState(D3DRENDERSTATE_SRCBLEND, D3DBLEND_ONE);
D3DDevice->SetRenderState(D3DRENDERSTATE_DESTBLEND, D3DBLEND_ONE);
		

• Für herkömmliche transparente Objekte wie buntes Glas geben Sie ein:

D3DDevice->SetRenderState(D3DRENDERSTATE_SRCBLEND, D3DBLEND_SRCALPHA);
D3DDevice->SetRenderState(D3DRENDERSTATE_DESTBLEND, D3DBLEND_INVSRCALPHA);
		

Es gibt noch viele andere Kombinationen, doch nicht jede Grafikkarte unterstützt alle. Werfen Sie deshalb einen Blick in die Hilfefunktion des DX7-SDK. Zusätzlich fragen Sie beim Programmstart ab, welche der Device Caps (vgl. PC Underground 6/00, S. 246) die Hardware bedienen kann.

Alphatesting

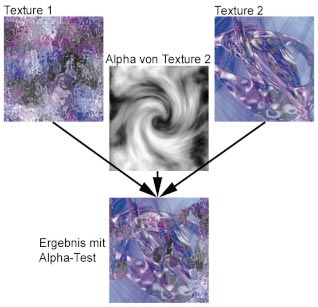
Eine weitere Anwendung für den Alphakanal ist das Alphatesting. Dabei machen Sie vom Alphawert eines Texels abhängig, ob dieser gezeichnet werden soll: Entweder soll der Texel vollständig opak oder transparent erscheinen.

Dazu legen Sie einen Referenzwert fest, der bestimmt, ob die zu zeichnenden Texel einen kleineren, größeren oder gleichen Alphawert aufweisen müssen. Normalerweise verwenden Sie die Alphatest-Funktionalität dazu, um Ränder von 3D-Objekten über der Textur feiner zu zeichnen, als dies mit einer erträglichen Anzahl von Polygonen machbar wäre. Wir wollen zwei Bitmaps ineinander überblenden.

Im Bild unten links sehen Sie zwei Texturen, die übereinander gezeichnet werden. Der zweiten Textur weisen Sie die Alphawerte zu, die Sie in der Mitte als Graustufenbild sehen. Dann schalten Sie den Alphatest ein, um den Alpha-Referenzwert zwischen 0 und 255 zu variieren. Dadurch erhalten Sie den Effekt, dass sich die zweite Textur Stück für Stück nach einem nicht gleich erkennbaren Muster über die erste ergießt. Der Code dazu lautet:

D3DTLVERTEX vQuad[4];
// vQuad: Rechteck-Koordinaten für FullScreen füllen
D3DDevice->SetRenderState(D3DRENDERSTATE_ALPHABLENDENABLE, FALSE);
D3DDevice->SetRenderState(D3DRENDERSTATE_ ALPHATESTENABLE, FALSE);

// erstes Mal zeichnen
D3DDevice->SetTexture(0, textur1);
D3DDevice->DrawPrimitive(D3DPT_TRIANGLEFAN, D3DFVF_TLVERTEX, vQuad, 4, 0);

// Alpha Test anschalten
D3DDevice->SetRenderState(D3DRENDERSTATE_ALPHATESTENABLE, TRUE);
D3DDevice->SetRenderState(D3DRENDERSTATE_ALPHAFUNC, D3DCMP_GREATER);
D3DDevice->SetRenderState(D3DRENDERSTATE_ALPHAREF, AlphaRef);

//mit zweiter Textur zeichnen
D3DDevice->SetTexture(0, textur2);
D3DDevice->DrawPrimitive(D3DPT_TRIANGLEFAN, D3DFVF_TLVERTEX, vQuad, 4, 0);
		

Damit sind die wichtigsten Prinzipien des Alpha-Blending umrissen. Um interessante Effekte zu erzielen, verändern Sie Parameter und Texturen. Die Mittel dazu gibt Ihnen das Programm an die Hand.

Multitexturing

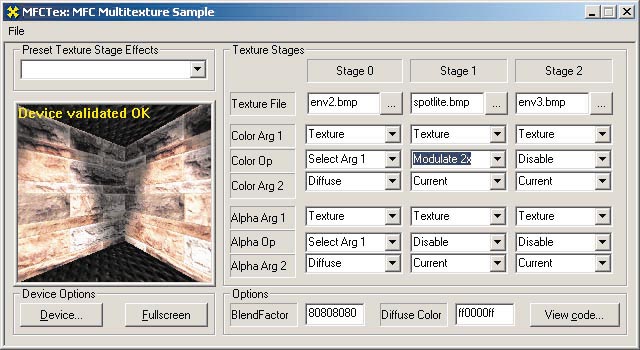
Weitere schöne Effekte erzielen Sie dadurch, dass Sie nicht nur eine einzige Textur verwenden, sondern einem Objekt mehrere zuordnen. Das ließe sich zwar alles auf einer Textur darstellen, doch verwenden Sie lieber mehrere Texturen.

Keine 3D-Beschleuniger­karte verfügt über unbegrenzten Texturspeicher. Wenn Sie Texturen im Hauptspeicher halten, bremst das Verfahren trotz relativ schnellem Datentransport über den PCI- oder AGP-Bus immer noch den Bildaufbau aus.

Stellen Sie sich ein Objekt vor, das eine Textur wie eine Steinmauer mitbringen soll. Nun wollen Sie Lichteffekte auf diese Mauer fallen lassen, wozu Sie eine sogenannte Lightmap verwenden. Die Lightmap ist eine viel kleinere Textur, die sich aber auch über die gesamte Mauer erstreckt und nur Helligkeits­infomationen enthält. Diese Textur ist kleiner, weil sie dynamisch berechnet werden soll. Erst beide Texturen zusammen ergeben den erwünschten Effekt. Das Programm MFCTEX lässt Sie mehrere Texturen gleichzeitig kombinieren. Sie können sich sogar den Quellcode für die entsprechende Einstellung ausgeben lassen. Wenn Sie mehrere Texturen verwenden, heißt dieses Verfahren Multitexturing. Spiegeln Sie Effekte: Wenn Sie ein Objekt schon mit eigener Textur versehen haben, brauchen Sie dazu eine zweite Textur. Wenn Sie Texturen spiegeln wollen, nennt sich dieser Vorgang Environment Mapping, weil die Umgebung auf der Texture-Map zu sehen ist.

Für diese Effekte müssen Sie Ihrem 3D-Objekt zwei Sätze von Textur­koordinaten zuweisen. Zuerst legen Sie einen Vertex-Buffer wie folgt an:

D3DVERTEXBUFFERDESC vbdesc;
vbdesc.dwSize = sizeof(vbdesc);
vbdesc.dwCaps = 0;
vbdesc.dwFVF = D3DFVF_XYZ | D3DFVF_NORMAL | D3DFVF_TEX2;
vbdesc.dwNumVertices = 20000;
D3D7->CreateVertexBuffer(&vbdesc, (IDirect3DVertexBuffer7**)&pVertexBuffer, 0);
		

Dabei verwenden Sie ein Format für die Vertices (Eckpunkte), das Sie noch definieren müssen.

typedef struct
{
// Koordinaten
D3DVALUE dvX, dvY, dvZ;
// Normale
D3DVALUE dvNX, dvNY, dvNZ;
// Texturkoordinaten
D3DVALUE
	dvTU, dvTV, dvTU2, dvTV2;
} D3DVERTEX2;
		

Folgendermaßen spiegeln Sie Effekte über eine Environment Map: Sie berechnen eine Textur mit einem zweiten Satz von Textur­koordinaten abhängig von der Position des Betrachters und der Objektrotation für jedes Bild neu. Den Vertex-Buffer können Sie nicht von Direct3D per Optimize(...) optimieren, da Sie sonst nicht mehr auf dessen Inhalt zugreifen dürfen.

Im Gegensatz zur Bewegung der Kamera (vgl. Heft 6/00, S. 246) kehren Sie jetzt die Trans­formationen um, um die Textur­koordinaten zu berechnen. Sie können eine Hälfte des drei­dimensionalen Raums in einer Textur halten. Der Blickwinkel geht hierbei vom spiegelnden Objekt aus, wobei Sie ein recht verzerrtes Bild erhalten. Die dazugehörigen Textur­koordinaten berechnen Sie wie folgt.

//Kamera- und Objektbewegung
D3DXMATRIX amatWorld, amatView, matWV;
D3DDevice->GetTransform(D3DTRANSFORMSTATE_VIEW, amatView);
D3DDevice->GetTransform(D3DTRANSFORMSTATE_WORLD, amatWorld);
D3DXMatrixMultiply (&matWV, &amatWorld, &amatView );
//Normalen drehen und Texturkoordinaten
// für jede Normale (nx,ny,nz)
dvTU2 = 0.5f * (1.0f + (nx * matWV.m[0][0] + ny *
	matWV.m[1][0] + nz*matWV.m[2][0]));
dvTV2 =0.5f * (1.0f - (nx * matWV.m[0][1] + ny *
	matWV.m[1][1] + nz * matWV.m[2][1]));
		

Im Bild unten sehen Sie einen verschlungenen Knoten (Torusknoten) mit einer Environment Map. Das Bild enthält nur eine Lichtquelle. Mit zwei Texturen erzielen Sie schon einfache Beleuchtungs­effekte. Die Beleuchtung ist eine Nachahmung der Phong-Beleuchtung, die über Environment Maps nur von den neuesten 3D-Beschleunigern unterstützt wird.

Marching-Cubes Algorithmus

Jetzt starten Sie unser Beispiel­programm und beobachten, wie sich die sichtbaren Kugeln bewegen und miteinander verschmelzen. Diese 3D-Objekte berechnet der Marching-Cubes-Algorithmus. Ihn haben William E. Lorensen und Harvey E. Cline entwickelt, um Flächen­informationen aus einem drei­dimensionalem Feld zu berechnen. Die Fläche (Isofläche genannt) taucht überall dort auf, wo innerhalb des Felds ein Wert vorliegt. Marching-Cubes-Algorithmus wird vorwiegend bei der medizinischen Daten­verarbeitung, geologischen Scans und zur Visualisierung von Äquipotential­flächen elektrischer Felder und Ladungen verwendet.

Die Eingabedaten enthalten einen Referenzfloat-Wert, auf dem die Isofläche liegen soll. Es wird untersucht, ob ein Punkt im Eingabefeld innerhalb oder außerhalb der Isofläche liegt, also sein Wert kleiner oder größer als der Referenzwert ist.

Der Marching-Cubes-Algorithmus unterteilt den betrachteten Raum in kleine Würfel. Überprüfen Sie für die Eckpunkte jedes Würfels, ob sie innerhalb oder außerhalb der Isofläche liegen. Dann ersetzen Sie den Würfel durch eine Reihe von Polygonen.< Alle so generierten Polygone stellen angenähert die Isofläche dar.

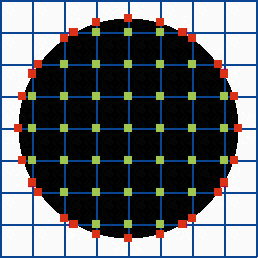
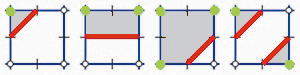
Im Bild oben sehen Sie ein Gitter mit einem einge­zeichneten Kreis, den Linien annähernd darstellen sollen. Berechnen Sie für alle Eckpunkte die Gitterquadrate, welche grüne Punkte symbolisieren. Diese liegen innerhalb oder außerhalb des Kreises. Fügen Sie Start- und Eckpunkte für die Linien ein, die dem Schema entsprechen.

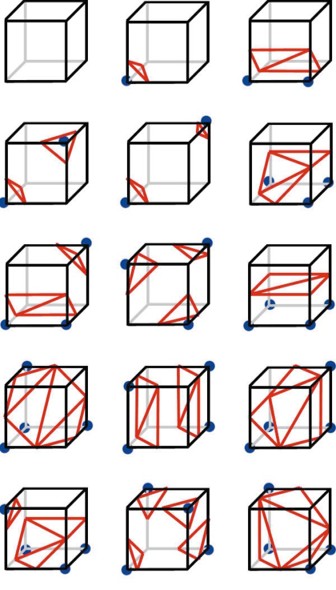
Wenn Sie die Punkte zu einem Linienzug verbinden, sehen Sie ungefähr den Kreisrand. Diese Vorgehensweise übertragen Sie auf die dritte Dimension. Da ein Würfel acht Ecken hat, und jede der Ecken entweder innerhalb oder außerhalb liegen kann, müssen Sie maximal 2⁸ = 256 Fallunter­scheidungen berechnen. Gehen Sie zunächst von 15 Basisfällen aus, die das folgende Bild verdeutlicht. Alle anderen Kombinationen erhalten Sie durch Drehung, Spiegelung und Vertauschen von inneren und äußeren Perspektiven.

Um die Isofläche einfacher berechnen zu können, speichern Sie alle Fälle in Tabellen. Sie finden die Tabelle im Quellcode unseres Beispiel­programms auf der Heft-CD.

Die Tabelle in unserem Beispiel­programm liefert für jeden der 256 Fälle eine Liste mit Polygonkanten. Die Darstellung kann zwischen null und vier Dreiecke für einen Würfel erfordern. Eine zweite Tabelle dient dazu, die Eckpunkte für die Kanten zu finden. Die Qualität der Darstellung verbessern Sie, indem Sie die Eckpunkte der Polygone verschieben. Im zwei­dimensionalen Beispiel verändern Sie Start-/Endpunkte der Linien.

Sie legen fest, ob Eckpunkte innerhalb oder außerhalb der Körper oder Flächen liegen. Es ist damit nicht gewährleistet, dass der Referenzwert genau zwischen den Gitterpunkten liegt. Setzen Sie den Eckpunkt also nicht ganz genau in der Mitte an.

Einfacher, aber dennoch gut ist es, den Verlauf der float-Werte zwischen zwei Gitterpunkten als linear anzunehmen. Dann können Sie durch eine einfache Quotienten­bildung eine bessere Position für den Eckpunkt berechnen.

Abschließend stellen Sie dem Programm die Eingabedaten zur Verfügung. Dabei handelt es sich um ein drei­dimensionales Array von float-Werten. Anfangs setzen Sie jeden Eintrag auf den Wert 0. Übergeben Sie alle Einträge mit den Koordinaten x, y, z, deren Werte Sie nach weiteren Vorlagen ändern. Für eine punktförmige elektrische Ladung verwenden Sie folgende Formel:

// Position der Ladung: tx1, ty1, tz1
Feld[z][y][x] = 1.0f / ((x - tx1) * (x - tx1) +
	(y + ty1) * (y + ty1) + (z - tz1) * (z - tz1));
		

Das Beispiel­programm stellt vier dieser Ladungen dar. Sie können nicht nur Kugeln darstellen, sondern alle mathematischen impliziten Flächen wie einen Torus oder Kegel (implizit beschreibt Formen, welche mathematische Funktionen darstellen können). Experimentieren Sie mit den Einstellungen und Renderstates.